Organic catalysis is a major topic of Chapter 5 of my book. The use of iminium ions as a catalyst and to provide stereoselection, pioneered by MacMillan,¹ was not discussed in the book.

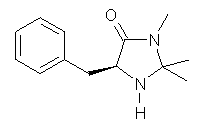
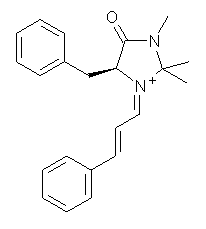
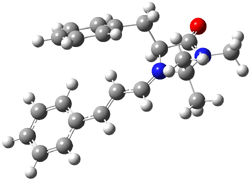
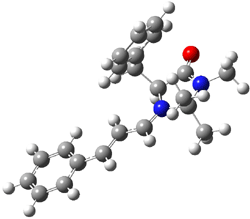
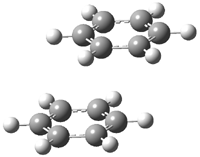
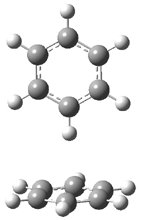
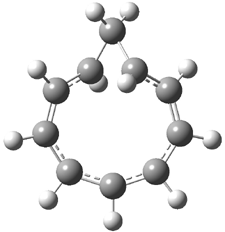
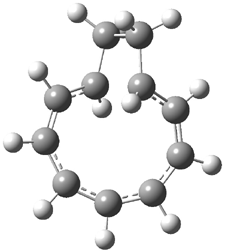
Macmillan had proposed that the iminium 2 formed of imidazolinone 1 and (E)-3-phenylprop-2-enal has conformation A. This conformation blocks access to one face of the alkene and directs, for example, dienophiles to the opposite face. Houk found that conformer B is lower in energy at B3LYP/6-31G(d).²

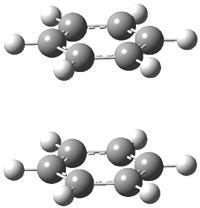
Now Tomkinson³ has produced a study that convincingly shows that 2 exists as conformer B. An x-ray structure shows this conformation in the solid state. Proton NMR shows that the methyl group signals are interpretable only as coming from B. Finally, SCS-MP2/aug-cc-pVTZ//BHandH/6-31+G(d,p) (see Figure 1) computations show that B is 1.2 kcal mol^-1 more stable than A in the gas phase, and PCM computations indicate that this gap is reduced by less then 0.5 kcal mol^-1 in methanol or acetonitrile.

Conformation B provides little steric hindrance at the β-carbon of the iminium ion, explaining its poor stereoselectivity in conjugate additions.

A

B

Figure 1. BHandH/6-31+G(d,p) optimized structures of conformers A and B of 2.

References

(1) Ahrendt, K. A.; Borths, C. J.; MacMillan, D. W. C., "New Strategies for Organic Catalysis: The First Highly Enantioselective Organocatalytic Diels-Alder Reaction," J. Am. Chem. Soc., 2000, 122, 4243-4244, DOI: 10.1021/ja000092s.

(2) Gordillo, R.; Houk, K. N., "Origins of Stereoselectivity in Diels-Alder Cycloadditions Catalyzed by Chiral Imidazolidinones," J. Am. Chem. Soc., 2006, 128, 3543-3553, DOI: 10.1021/ja0525859.

(3) Brazier, J. B.; Evans, G.; Gibbs, T. J. K.; Coles, S. J.; Hursthouse, M. B.; Platts,
J. A.; Tomkinson, N. C. O., "Solution Phase, Solid State, and Theoretical Investigations on the MacMillan Imidazolidinone," Org. Lett., 2009, 11, 133-136, DOI: 10.1021/ol802512y.

InChIs

1: InChI=1/C13H18N2O/c1-13(2)14-11(12(16)15(13)3)9-10-7-5-4-6-8-10/h4-8,11,14H,9H2,1-3H3/t11-/m0/s1
InChIKey=UACYWOJLWBDSHG-NSHDSACABQ

2: InChI=1/C22H25N2O/c1-22(2)23(3)21(25)20(17-19-13-8-5-9-14-19)24(22)16-10-15-18-11-6-4-7-12-18/h4-16,20H,17H2,1-3H3/q+1/b15-10+,24-16+/t20-/m0/s1
InChIKey=ZPEHVNACGWTABV-BYFMJTDEBT

Here’s a nice example of the application of computed solvation energies in non-aqueous studies. Cramer and Truhlar have employed their latest SM8 technique, which is parameterized for organic solvents and for water, to estimate solvation energies in olive oil.¹ Now you may wonder why solvation in olive oil of all things? But the partitioning of molecules between water and olive oil has been shown to be a good predictor of lipophilicity and therefore bioavailability of drugs! The model works reasonably well in reproducing experimental solvation energies and partition coefficients. They do make the case that fluorine substitution which appears to improve solubility in organics,originates not to more favorable solvation in organic solvents (like olive oil) but rather that fluorine substitution dramatically decreases solubility in water.

References

(1) Chamberlin, A. C.; Levitt, D. G.; Cramer, C. J.; Truhlar, D. G., "Modeling Free Energies of Solvation in Olive Oil," Mol. Pharmaceutics, 2008, 5, 1064-1079, DOI: 10.1021/mp800059u

Liu has provided the link between pure the prototype organic aromatic compound (benzene) and the prototype pure inorganic aromatic (borazine).¹ His group has prepared 1,2-dihydro1,2-azaborine 1. Dixon has performed computations to support the identification of the molecule. For example, the computed and experimental chemical shifts are in nice agreement (see Table 1). The B3LYP/DZVP2 optimized structure of 1 is shown in Figure 1.

Table 1. Computed^a and experimental chemical shifts (ppm) of 1.¹

^aB3LYP/Alhrichs-vTZP.

Figure 1. B3LYP/DZVP2 optimized structure of 1.¹

The computations support the notion that 1 is truly aromatic. Its NICS(1) value is -7.27 ppm, close that of benzene (-10.39 ppm), and much more negative that that of borazine (-3.01 ppm). Reactions 1 and 2 compare the stability of 1 to benzene. These indicate that the resonance stabilization energy of 1 is about 13 kcal mol^-1 less than that of benzene, whose RSE is about 34 kcal mol^-1. Liu and Dixon thus consider 1 to be an aromatic compound and one that helps create a sort of organic, mixed organic-inorganic and inorganic aromatic continuum.

References

(1) Marwitz, A. J. V.; Matus, M. H.; Zakharov, L. N.; Dixon, D. D.; Liu, S.-Y., "A Hybrid Organic/Inorganic Benzene," Angew. Chem. Int. Ed. 2009, 48, 973-977, DOI: 10.1002/anie.200805554

InChIs

1: InChI=1/C4H6BN/c1-2-4-6-5-3-1/h1-6H
InChIKey=OGZZEGWWYQKMSO-UHFFFAOYAN

The failure of DFT in dealing with some seemingly straightforward reactions (as discussed in these previous blog posts: A, B, C, D, E, F) has become a bit clearer. Brittain and co-workers have identified the culprit.¹ They examined twelve different reactions, involving neutral, radical, cations and anions:

R-Me + Me-H → R-H +Me-Me

R-Me + Me^. → R^. + Me-Me

R-Me + Me^– → R^– + Me-Me

R-Me + Me⁺ → R⁺ + Me-Me

where R is ethyl, i-propyl and t-butyl. They used a variety of different functionals, and benchmarked the energies against those found at CCSD(T)/cc-pVTZ. By systematically using different densities and different exchange and correlation components, DFT exchange is responsible for the poor performance – and it can be very poor: the error for the cation reaction with R=t-butyl is 12 kcal mol^-1 with B3LYP and 18 kcal mol^-1 with PBE. It should be noted that the maximum error with G3(MP2) and MP2 is 1.5 and 2.5 kcal mol^-1, respectively. These authors make three important conclusions: (a) that traditional ab initio methods are preferred, (b) that development of new functionals should target the exchange component, and (c) Truhlar’s highly parameterized functional MO5-2X works quite well (maximum error is 2.6 kcal mol^-1 – again for the cation t-butyl case) but the reason for its success is unknown.

References

(1) Brittain, D. R. B.; Lin, C. Y.; Gilbert, A. T. B.; Izgorodina, E. I.; Gill, P. M. W.; Coote, M. L., "The role of exchange in systematic DFT errors for some organic reactions," Phys. Chem. Chem. Phys. 2009, DOI: 10.1039/b818412g.

Here’s another great example of synthesis of highly strained compounds. Bertrand has prepared the substituted triafulvalene 1.¹ The compound is stable as a solid or in solution under inert gas. It does however react quickly with water, a remarkable addition of water across an alkene. This is understood in terms of a very high HOMO and a low LUMO, indicating a very reactive double bond. The UV/Vis corroborates this: its absorption is at 502nm, compared to 171nm of ethylene and 217nm of 1,3-butadiene. The B3LYP/6-31G(d) structure of the tetraphenyl derivative 2 is shown in Figure 1.

1

2

Figure 1. B3LYP/6-31G(d) optimized structure of 2.

References

(1) Kinjo, R.; Ishida, Y.; Donnadieu, B.; Bertrand, G., "Isolation of Bicyclopropenylidenes: Derivatives of the Smallest Member of the Fulvalene Family," Angew. Chem. Int. Ed. 2009, 48, 517-520, DOI: 10.1002/anie.200804372

InChIs

1: InChIKey=GJHAFFXCMBMUNM-DBFBYELTBP

2: InChIKey=WTGGHSXPMAHUNP-UHFFFAOYAY

Malonaldehyde 1 possesses a very short intramolecular hydrogen bond. Its potential energy surface has two local minima (the two mirror image hydrogen-bonded structures) separated by a C_2v transition state. Schaefer reports a high-level computational study for the search for even shorter hydrogen bonds that might even lead to a single well on the PES.¹

The hydrogen bond distance is characterized by the non-bonding separation between the two oxygen atoms. Table 1 shows the O^…O distance for a number of substituted malonaldehydes computed at B3LYP/DZP++. Electron withdrawing groups on C₂ reduce the O^..O distance (see trend in 1 → 4). Electron donating groups on C₁ and C₃ also reduce this distance (see 5 and 6). Bulky substituents on the terminal carbons also reduce the O^…O distance (see 7). Combining all of these substituent effects in 8 leads to the very short O^…O distance of 2.380 Å.

Table 1. Distance (Å) between the two oxygen atoms and the barrier for hydrogen transfer of substituted malonaldehydes .¹

^aFocal point energy. ^bFocal point energy and corrected for zero-point vibrational energy.

A shorter O^…O distance might imply a smaller barrier for hydrogen transfer between the two oxygens. The structures of 8 and the transition state for its hydrogen transfer are shown in Figure 1. The energies of a number of substituted malonaldehydes were computed using the focal point method, and the barriers for hydrogen transfer are listed in Table 1. There is a nice correlation between the O^…O distance and the barrier height. The barrier for 8 is quite small, suggesting that with some bulkier substituents, the barrier might vanish altogether, leaving only a symmetric structure. In fact, the barrier appears to vanish when zero-point vibrational energies are included.

8

8TS

Figure 1. B3LYP/DZP++ optimized geometries of 8 and the transition state for hydrogen transfer 8TS.¹

References

(1) Hargis, J. C.; Evangelista, F. A.; Ingels, J. B.; Schaefer, H. F., "Short Intramolecular Hydrogen Bonds: Derivatives of Malonaldehyde with Symmetrical Substituents," J. Am. Chem. Soc., 2008, 130, 17471-17478, DOI: 10.1021/ja8060672.

InChIs

1: InChI=1/C3H4O2/c4-2-1-3-5/h1-4H/b2-1-
InChIKey=GMSHJLUJOABYOM-UPHRSURJBI

2: InChI=1/C4H3NO2/c5-1-4(2-6)3-7/h2-3,6H/b4-2-
InChIKey=BHYIQMFSOGUTRT-RQOWECAXBC

3: InChI=1/C3H3NO4/c5-1-3(2-6)4(7)8/h1-2,5H/b3-1+
InChIKey=JBBHDCMVSJADCE-HNQUOIGGBS

4: InChI=1/C3H5BO2/c4-3(1-5)2-6/h1-2,5H,4H2/b3-1+
InChIKey=IQNKNZSFMBIPBI-HNQUOIGGBX

5: InChI=1/C3H6N2O2/c4-2(6)1-3(5)7/h1,6H,4H2,(H2,5,7)/b2-1-/f/h5H2
InChIKey=AOZIOAJNRYLOAH-KRHGAQEYDI

6: InChI=1/C5H8O4/c1-8-4(6)3-5(7)9-2/h3,6H,1-2H3/b4-3+
InChIKey=BYYYYPBUMVENKB-ONEGZZNKBI

7: InChI=1/C11H20O2/c1-10(2,3)8(12)7-9(13)11(4,5)6/h7,12H,1-6H3/b8-7-
InChIKey=SOZFXLUMSLXZFW-FPLPWBNLBX

8: InChI=1/C3H5N3O4/c4-2(7)1(3(5)8)6(9)10/h7H,4H2,(H2,5,8)/b2-1+/f/h5H2
InChIKey=IHYUFGCOUITNJP-CHFMFTGODK

The nature of the bridgehead-bridgehead bond in [1.1.1]propellane 1 poses an interesting quandary. The bond involves two inverted carbon atoms, whose hybrids should point away from each other. The internuclear region has in fact much less electron density than for an ordinary C-C bond. Nonetheless, the molecule is stable and the C-C bond is estimated to have a strength of about 6 kcal mol^-1.

Shaik and Hiberty¹ have now proposed that the central C-C bond of [1.1.1]propellane is a charge-shift bond. In classical valence bond theory, we have three configurations for a bond: the covalent structure A↑↓B ↔ A↓↑B, and the two ionic structures A↑↓ B and A B↑↓. The description of a typical covalent bond is dominated by the covalent VB structure with a little bit of the ionic structures mixed in. A charge-shift bond is one where the resonance energy due to the mixing of the covalent and ionic structures mostly accounts for the stabilization of the bond.² Just such a case is found in the F-F bond, and also to for the central C-C bond of [1.1.1]propellane!

References

(1) Wu, W.; Gu, J.; Song, J.; Shaik, S.; Hiberty, P. C., "The Inverted Bond in [1.1.1]Propellane is a Charge-Shift Bond," Angew. Chem. Int. Ed., 2008, ASAP DOI: 10.1002/anie.200804965

(2) Shaik, S.; Danovich, D.; Silvi, B.; Lauvergnat, D. L.; Hiberty, P. C., "Charge-Shift Bonding – A Class of Electron-Pair Bonds That Emerges from Valence Bond Theory and Is Supported by the Electron Localization Function Approach," Chem. Eur. J., 2005, 11, 6358-6371, DOI: 10.1002/chem.200500265

InChI

1: InChI=1/C5H6/c1-4-2-5(1,4)3-4/h1-3H2
InChIKey=ZTXSPLGEGCABFL-UHFFFAOYAJ

In sort of an afterword to a recent publication, Stanger¹ points out an error made by Hückel in arguing for stability of D_6h benzene over the hypothetical D_3h cyclohexatriene. Hückel constructed the first two matrices shown below to describe each molecule. The energy of benzene, predicted by this matrix, is 6α-8β, which is lower than that for cyclohexatriene, 6α-6β.

Stanger points out that implicit in Hückel’s argument is that the value of the H_ij element for the double bond is identical in value for the two compounds, (namely β), and the element is zero for the single bonds. Considering that the C-C double bond in cyclohexatriene should be shorter than that in benzene, Stanger suggests that its H_ij element should be larger than β and the H_ij element for the single bond should not be zero, but some small value reflecting the overlap between the p-orbitals. He suggests that the values for the single and double bond elements should be 0.4589β and 1.5050β, giving the bottom matrix below. This leads to an electronic energy of 6α-9.212β. In other words, this more appropriate model of cyclohexatriene has a lower π energy than does D_6h benzene! This is in accord with Shaik’s argument² that the π system of benzene acts to localize the bonds and it’s the σ system that is responsible for its delocalized structure.

Figure 1. Hückel matrices and eigenvalues for benzene (top),
traditional cyclohexatriene model (middle), and revised cyclohexatriene model (bottom).¹

References

(1) Stanger, A., "The Different Aromatic Characters of Some Localized Benzene Derivatives&#x2020," J. Phys. Chem. A, 2008, 112, 12849-12854, DOI: 10.1021/jp801634x

(2) Shaik, S.; Shurki, A.; Danovich, D.; Hiberty, P. C., "A different story of benzene," Journal of Molecular Structure: THEOCHEM, 1997, 398-399, 155-167, DOI: 10.1016/S0166-1280(96)04934-2.

Hobza¹ has published a very high-level computational study of the benzene dimer as a benchmark for this model of π-π stacking – a topic I have touched upon a number of times in this blog (post 1, post 2) . There are four local energy minima, shown in Figure 1. The most stable dimer is the tilted T-structure (TT), a structure often overlooked. Its complexation energy, computed at CCSD(T)/CBS, is 2.78 kcal mol^-1. Only slightly higher in energy is the parallel displaced structure (PD), with a stabilization energy of 2.70 kcal mol^-1. The T structure (T) is essentially isoenergetic with the PD one. The perfectly stacked structure (S) is much less stable, with a dimerization energy of 1.64 kcal mol^-1. The DTF-D method, using the BLYP functional with dispersion parameters optimized for the benzene dimer provide energies within 0.2 kcal mol^-1 of the computationally much more expensive benchmark values. As a word of caution though: use of more general dispersion parameters gives energies far worse and predicts the wrong energy order of the dimers.

TT 2.78 2.93 2.33	PD 2.70 2.88 2.57
T 2.69 2.80 2.03	S 1.64 1.84 1.45

Figure 1. Structures of the benzene dimer with stabilization energy (kcal mol^-1) computed at CCSD(T)/CBS (bold), DFT-D/BLYP with optimized parameters (italics), and DFT-D/BLYP with general parameters (plain).¹

References

(1) Pitonak, M.; Neogrady, P.; Rexac, J.; Jurecka, P.; Urban, M.; Hobza, P., "Benzene Dimer: High-Level Wave Function and Density Functional Theory Calculations," J. Chem. Theory Comput., 2008, 4, 1829-1834, DOI: 10.1021/ct800229h.

Rzepa has extended the concept of Möbius aromaticity to homoaromaticity.¹ 1 is the homoaromatic analogue of the tropylium cation. Topoligical electron density analysis, also known as Atoms-In-Molecules (AIM), indicates no bond path connecting C₁and C₇. However, the NICS value at the ring critical point of 1 is -11.5 ppm, indicative of aromaticity. 2 is the potential Möbius aromatic analogue of 1. Unlike 1 which has a plane of symmetry, 2 has a C₂ rotational axis of symmetry, as anticipated for a Möbius homoaromatic compound. However, there is no bond path connecting C₁ with C₉. But, the NICS value at the ring critical point of 2 is -11.3 ppm, supporting the notion of aromatic character! Suprisingly, the AIM analysis of the larger homologue 3 does have a bond path connecting C₁ to C₉, even though the distance separating these compounds is larger than in 2! Again the NICS value for 3 is negative (-9.8) and so it certainly appears to be Möbius homoaromatic.

The B3LYP/aug-cc-pVYZ structures of 1-3 are shown in Figure 1. As is Rzepa’s practice, he provides an extensive collection of data on the molecules he reports making great use of electronic depositories, and it looks like the ACS has now moved this “web-enhanced table” out into the open part of its web site: http://pubs.acs.org/doi/suppl/10.1021/ct8001915/suppl_file/index.html.

1	2
3

Figure 1. B3LYP/aug-cc-pVYZ optimized structures of 1-3.¹

References

(1) Allan, C. S. M.; Rzepa, H. S., "Chiral Aromaticities. A Topological Exploration of Möbius Homoaromaticity," J. Chem. Theory Comput., 2008, 4, 1841-1848, DOI: 10.1021/ct8001915

InChIs

1: InChI=1/C8H9/c1-2-4-6-8-7-5-3-1/h1-7H,8H2/q+1/b2-1-,5-3-,6-4-
InChIKey=ZINXKSGXPFSBNB-XCADPSHZBA

2: InChI=1/C10H11/c1-2-4-6-8-10-9-7-5-3-1/h1-9H,10H2/q+1/b2-1-,5-3-,6-4-,9-7-
InChIKey=HBJCUFQWAIKURE-BWYSQNKRBE

3: InChI=1/C11H13/c1-2-4-6-8-10-11-9-7-5-3-1/h1-9H,10-11H2/q+1/b2-1-,5-3-,6-4-,9-7-InChIKey=LUGAIBOLHSLVBJ-BWYSQNKRBF