Truhlar has made a comparison of binding energies and relative energies of five (H₂O)₁₆ clusters.¹ While technically not organic chemistry, this paper is of interest to the readership of this blog as it compares a very large collection of density functionals on a problem that involves extensive hydrogen bonding, a problem of interest to computational organic chemists.

The CCSD(T)/aug-cc-pVTZ//MP2/aug-cc-pVTZ energies of clusters 1-5 (shown in Figure 1) were obtained by Yoo.² These clusters are notable not just for their size but also that they involve multiple water molecules involved in four hydrogen bonds. Truhlar has used these geometries to compute the energies using 73 different density functionals with the jun-cc-pVTZ basis set (see this post for a definition of the ‘jun’ basis sets). Binding energies (relative to 16 isolated water molecules) were computed along with the 10 relative energies amongst the 5 different clusters. Combining the results of both types of energies, Truhlar finds that the best overall performance relative to CCSD(T) is obtained with ωB97X-D, a hybrid GGA method with a dispersion correction. The next two best performing functionals are LC-ωPBE-D3 and M05-2x. The best non-hybrid performance is with revPBE-D3 and B97-D.

1 (0.0)	2 (0.25)
3 (0.42)	4 (0.51)
5 (0.54)

Figure 1. MP2/aug-cc-pVTZ optimized geometries and relative CCSD(T) energies (kcal mol^-1) of (water)₁₆ clusters 1-5. (Don’t forget to click on any of these molecules above to launch Jmol to interactively view the 3-D structure. This feature is true for all molecular structures displayed in all of my blog posts.)

While this study can help guide selection of a functional, two words of caution. First, Truhlar notes that the best performing methods for the five (H₂O)₁₆ clusters do not do a particularly great job in getting the binding and relative energies of water hexamers, suggesting that no single functional really stands out as best. Second, a better study would also involve geometry optimization using that particular functional. Since this was not done, one can garner little here about what method might be best for use in a typical study where a geometry optimization must also be carried out.

References

(1) Leverentz, H. R.; Qi, H. W.; Truhlar, D. G. "Assessing the Accuracy of Density
Functional and Semiempirical Wave Function Methods for Water Nanoparticles: Comparing Binding and Relative Energies of (H₂O)₁₆ and (H₂O)₁₇ to CCSD(T) Results," J. Chem. Theor. Comput. 2013, ASAP, DOI: 10.1021/ct300848z.

(2) Yoo, S.; Aprà, E.; Zeng, X. C.; Xantheas, S. S. "High-Level Ab Initio Electronic Structure Calculations of Water Clusters (H₂O)₁₆ and (H₂O)₁₇: A New Global Minimum for (H₂O)₁₆," J. Phys. Chem. Lett. 2010, 1, 3122-3127, DOI: 10.1021/jz101245s.

This is a short post mainly to bring to the reader’s attention a couple of recent JCTC papers.

The first is a benchmark study by Hujo and Grimme of the geometries produced by DFT computations that are corrected for dispersion.¹ They use the S22 and S66 test sets that span a range of compounds expressing weak interactions. Of particular note is that the B3LYP-D3 method provided the best geometries, suggesting that this much (and justly) maligned functional can be significantly improved with just the simple D3 fix.

The second paper entails the description of Truhlar and Cramer’s latest iteration on their solvation model, namely SM12.² The main change here is the use of Hirshfeld-based charges, which comprise their Charge Model 5 (CM5). The training set used to obtain the needed parameters is much larger than with previous versions and allows for treating a very broad set of solvents. Performance of the model is excellent.

References

(1) Hujo, W.; Grimme, S. "Performance of Non-Local and Atom-Pairwise Dispersion Corrections to DFT for Structural Parameters of Molecules with Noncovalent Interactions," J. Chem. Theor. Comput. 2013, 9, 308-315, DOI: 10.1021/ct300813c

(2) Marenich, A. V.; Cramer, C. J.; Truhlar, D. G. "Generalized Born Solvation Model SM12," J. Chem. Theor. Comput. 2013, 9, 609-620, DOI: 10.1021/ct300900e

How should one add diffuse functions to the basis set? Diffuse functions are known to be critical in describing the electron distribution of anions (as discussed in my book), but they are also quite important in describing weak interactions, like hydrogen bonds, and can be critical in evaluating activation barriers and other properties.

The Truhlar group has been active in benchmarking the need of basis functions and their recent review¹ summarizes their work. In particular, they recommend that for DFT computations a minimally augmented basis set is appropriate for examining barrier heights and weakly bound systems. A minimally augmented basis set would have s and p diffuse functions on heavy atoms for the Pople split-valence basis sets and the Dunning cc-pVxZ basis sets.

For wavefunction based computations, they recommend the use of the “jun-“ basis sets. The “jun” basis set is one of the so-called calendar basis set derived from the aug-cc-pVxZ, which includes diffuse functions of all types. So, for C in the aug-cc-pVTZ basis set, there are diffuse s, p, d, and f functions. The “jun-“ basis set omits the diffuse f functions along with all diffuse functions on H.

The great advantage of these trimmed basis sets is that they are smaller than the fully augmented sets, leading to faster computations. And since trimming off some diffuse functions leads to little loss in accuracy, one should seriously consider using these types of basis sets. As Truhlar notes, these trimmed basis sets might allow one to use a partially augmented but larger zeta basis set at the same cost of the smaller zeta basis that is fully augmented.

References

(1) Papajak, E.; Zheng, J.; Xu, X.; Leverentz, H. R.; Truhlar, D. G., "Perspectives on Basis Sets Beautiful: Seasonal Plantings of Diffuse Basis Functions," J. Chem. Theory Comput., 2011,
7, 3027-3034, DOI: 10.1021/ct200106a

Here’s a nice example of the application of computed solvation energies in non-aqueous studies. Cramer and Truhlar have employed their latest SM8 technique, which is parameterized for organic solvents and for water, to estimate solvation energies in olive oil.¹ Now you may wonder why solvation in olive oil of all things? But the partitioning of molecules between water and olive oil has been shown to be a good predictor of lipophilicity and therefore bioavailability of drugs! The model works reasonably well in reproducing experimental solvation energies and partition coefficients. They do make the case that fluorine substitution which appears to improve solubility in organics,originates not to more favorable solvation in organic solvents (like olive oil) but rather that fluorine substitution dramatically decreases solubility in water.

References

(1) Chamberlin, A. C.; Levitt, D. G.; Cramer, C. J.; Truhlar, D. G., "Modeling Free Energies of Solvation in Olive Oil," Mol. Pharmaceutics, 2008, 5, 1064-1079, DOI: 10.1021/mp800059u

Cramer and Truhlar have tested their latest solvation model SM8 against a test set of 17 small, drug-like molecules.¹ Their best result comes with the use of SM8, the MO5-2X functional, the 6-31G(d) basis set and CM4M charge model. This computational model yields a root mean squared error for the solvation free energy of 1.08 kcal mol^-1 across this test set. This is the first time these authors have recommended a particular computational model. Another interesting point is that use of solution-phase optimized geometries instead of gas-phase geometries leads to only marginally improved solvation energies, so that the more cost effective use of gas-phase structures is encouraged.

These authors note in conclusion that further improvement of solvation prediction rests upon “an infusion of new experimental data for molecules characterized by high degrees of functionality (i.e. druglike)”.

References

(1) Chamberlin, A. C.; Cramer, C. J.; Truhlar, D. G., “Performance of SM8 on a Test To Predict Small-Molecule Solvation Free Energies,” J. Phys. Chem. B, 2008, 112, 8651-8655, DOI: 10.1021/jp8028038.

Cramer and Truhlar¹ have published a nice review of their SM8 approach to evaluated solvation energy. Besides a quick summary of the theoretical approach behind the model, they detail a few applications. Principle among these is (a) the very strong performance of SM8 relative to some of the standard approaches in the major QM codes (see my previous blog post), (b) modeling interfaces, and (c) computing pK_a values of organic compounds.

References

(1) Cramer, C. J.; Truhlar, D. G., "A Universal Approach to Solvation Modeling," Acc. Chem. Res. 2008, 41, 760-768, DOI: 10.1021/ar800019z.

Truhlar and Cramer have updated their Solvation Model to SM8.¹ This model allows for any solvent to be utilized (both water and organic solvents) and treats both neutral and charged solutes. While there are some small theoretical changes to the model, the major change is in how the parameters are selected, the number of parameters, and a much more extensive data set is used for the fitting procedure.

Of note is how well this new model works. Table 1 compares the errors in solvation free energies computed using the new SM8 model against some other popular continuum methods. Clearly, SM8 provides much better results. As they point out, what is truly discouraging is the performance of the 3PM model against the continuum methods. 3PM stands for “three-parameter model”, where the solvation energies of all the neutral solute in water is set to their average experimental value (-2.99 kcal mol^-1), and the same for the neutral solutes in organic solvents (-5.38 kcal mol^-1), and for ions (-65.0 kcal mol^-1). The 3PM outperforms most of the continuum methods!

Table 1. Mean unsigned error (kcal mol^-1) for the solvation
free energies computed with different methods.¹

^a274 data points. ^b666 data points spread among 16 solvents. ^c332 data points spread among acetonitrile, water, DMSO, and methanol. ^dUsing mPW1PW/6-31G(d). ^eUsing mPW1PW/6-31G(d) and the UA0 atomic radii in Gaussian. ^fUsing mPW1PW/6-31G(d) and the UAHF atomic radii in Gaussian. ^gUsing B3LYP/6-31G(d) and conductor-PCM in GAMESS. ^hUsing B3LYP/6-31G(d) and the PB method in Jaguar.

References

(1) Marenich, A. V.; Olson, R. M.; Kelly, C. P.; Cramer, C. J.; Truhlar, D. G., "Self-Consistent Reaction Field Model for Aqueous and Nonaqueous Solutions Based on Accurate Polarized Partial Charges," J. Chem. Theory Comput., 2007, 3, 2011-2033. DOI: 10.1021/ct7001418.

We noted in Chapter 2.1 some serious errors in the prediction of bond dissociation energies using B3LYP. For example, Gilbert examined the C-C bond dissociation energy of some simple branched alkanes.¹ The mean absolute deviation (MAD) for the bond dissociation energy predicted by G3MP2 is 1.7 kcal mol^-1 and 2.8 kcal mol^-1 using MP2. In contrast, the MAD for the B3LYP predicted values is 13.7 kcal mol^-1, with some predictions in error by more than 20 kcal mol^-1. Furthermore, the size of the error increases with the size of the molecule. Consistent with this trend, Curtiss and co-workers noted a systematic underestimation of the heat of formation of linear alkanes of nearly 0.7 kcal mol^-1 per bond using B3LYP.²

Further evidence disparaging the general performance of DFT methods (and B3LYP in particular) was presented in a paper by Grimme and in two back-to-back Organic Letters articles, one by Schreiner and one by Schleyer. Grimme³ noted that the relative Energy of two C₈H₁₈ isomers, octane and 2,2,3,3-tetramethylbutane are incorrectly predicted by DFT methods (Table 1). While MP2 and CSC-MP2 (spin-component-scaled MP2) correctly predict that the more branched isomer is more stable, the DFT methods predict the inverse! Grimme attributes this error to a failure of these DFT methods to adequately describe medium-range electron correlation.

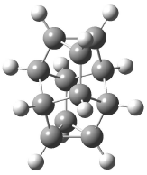
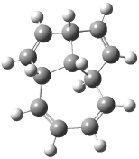
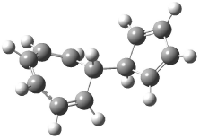
Schreiner⁵ also compared the energies of hydrocarbon isomers. For example, the three lowest energy isomers of C₁₂H₁₂ are 1-3, whose B3LYP/6-31G(d) structures are shown in Figure 1. What is disturbing is that the relative energies of these three isomers depends strongly upon the computational method (Table 2), especially since these three compounds appear to be quite ordinary hydrocarbons. CCSD(T) predicts that 2 is about 15 kcal mol^-1 less stable than 1 and that 3 lies another 10 kcal mol^-1 higher in energy. MP2 exaggerates the separation by a few kcal mol^-1. HF predicts that 1 and 2 are degenerate. The large HF component within B3LYP leads to this DFT method’s poor performance. B3PW91 does reasonably well in reproducing the CCSD(T) results.

1 xyz file

2 xyz file

3 xyz file

Figure 1. Structures of 1-3 at B3LYP/6-31G(d).

Another of Schreiner’s examples is the relative energies of the C₁₀H­₁₀ isomers; Table 3 compares their relative experimental heats of formation with their computed energies. MP2 adequately reproduces the isomeric energy differences. B3LYP fairs quite poorly in this task. The errors seem to be most egregious for compounds with many single bonds. Schreiner recommends that while DFT-optimized geometries are reasonable, their energies are unreliable and some non-DFT method should be utilized instead.

Schleyer’s example of poor DFT performance is in the isodesmic energy of Reaction 1 evaluated for the n-alkanes.⁶ The energy of this reaction becomes more positive with increasing chain length, which Schleyer attributes to stabilizing 1,3-interactions between methyl or methylene groups. (Schleyer ascribes the term “protobranching” to this phenomenon.) The stabilization energy of protobranching using experimental heats of formation increases essentially linearly with the length of the chain, as seen in Figure 2.

n-CH₃(CH₂)_mCH₃ + mCH₄ → (m + 1)C₂H₆         Reaction 1

Schleyer evaluated the protobranching energy using a variety of methods, and these energies are also plotted in Figure 2. As expected, the G3 predictions match the experimental values quite closely. However, all of the DFT methods underestimate the stabilization energy. Most concerning is the poor performance of B3LYP. All three of these papers clearly raise concerns over the continued widespread use of B3LYP as the de facto DFT method. Even the new hybrid meta-GGA functionals fail to adequately predict the protobranching phenomenon, leading Schleyer to conclude: “We hope that Check and Gilbert’s pessimistic admonition that ‘a computational chemist cannot trust a one-type DFT calculation’¹ can be overcome eventually”. These papers provide a clear challenge to developers of new functionals.

Figure 2. Comparison of computed and experimental protobranching stabilization energy (as defined in Reaction 1) vs. m, the number of methylene groups of the n-alkane chain.⁶

Truhlar believes that one of his newly developed functionals answers the call for a reliable method. In a recent article,⁴ Truhlar demonstrates that the M05-2X⁷ functional performs very well in all three of the cases discussed here. In the case of the C₈H₁₈ isomers (Table 1), M05-2X properly predicts that 2,2,3,3-tetramethylbutane is more stable than octane, and estimates their energy difference within the error limit of the experiment. Second, M05-2X predicts the relative energies of the C₁₂H₁₂ isomers 1-3 within a couple of kcal mol^-1 of the CCSD(T) results (see Table 2). Last, in evaluating the isodesmic energy of Reaction 1 for hexane and octane, M05-2X/6-311+G(2df,2p) predicts energies of 11.5 and 17.2 kcal mol^-1 respectively. These are in excellent agreement with the experimental values of 13.1 kcal mol^-1 for butane and 19.8 kcal mol^-1 for octane.

Truhlar has also touted the M05-2X functional’s performance in handling noncovalent interactions.⁸ For example, the mean unsigned error (MUE) in the prediction of the binding energies of six hydrogen-bonded dimers is 0.20 kcal mol^-1. This error is comparable to that from G3 and much better than CCSD(T). With the M05-2X functional already implemented within NWChem and soon to be released within Gaussian and Jaguar, it is likely that M05-2X may supplant B3LYP as the new de facto functional in standard computational chemical practice.

Schleyer has now examined the bond separation energies of 72 simple organic molecules computed using a variety of functionals,⁹ including the workhorse B3LYP and Truhlar’s new M05-2X. Bond separation energies are defined by reactions of each compound, such as three shown below:

The new M05-2X functional performed the best, with a mean absolute deviation (MAD) from the experimental energy of only 2.13 kcal mol^-1. B3LYP performed much worse, with a MAD of 3.96 kcal mol^-1. As noted before, B3LYP energies become worse with increasing size of the molecules, but this problem is not observed for the other functionals examined (including PW91, PBE, and mPW1PW91, among others). So while M05-2X overall appears to solve many of the problems noted with common functionals, it too has some notable failures. In particular, the error is the bond separation energies of 4, 5, and 6 is -8.8, -6.8, and -6.0 kcal mol^-1, respectively.

References

(1) Check, C. E.; Gilbert, T. M., “Progressive Systematic Underestimation of Reaction Energies by the B3LYP Model as the Number of C-C Bonds Increases: Why Organic Chemists Should Use Multiple DFT Models for Calculations Involving Polycarbon Hydrocarbons,” J. Org. Chem. 2005, 70, 9828-9834, DOI: 10.1021/jo051545k.

(2) Redfern, P. C.; Zapol, P.; Curtiss, L. A.; Raghavachari, K., “Assessment of Gaussian-3 and Density Functional Theories for Enthalpies of Formation of C₁-C₁₆ Alkanes,” J. Phys. Chem. A 2000, 104, 5850-5854, DOI: 10.1021/jp994429s.

(3) Grimme, S., “Seemingly Simple Stereoelectronic Effects in Alkane Isomers and the Implications for Kohn-Sham Density Functional Theory,” Angew. Chem. Int. Ed. 2006, 45, 4460-4464, DOI: 10.1002/anie.200600448

(4) Zhao, Y.; Truhlar, D. G., “A Density Functional That Accounts for Medium-Range Correlation Energies in Organic Chemistry,” Org. Lett. 2006, 8, 5753-5755, DOI: 10.1021/ol062318n

(5) Schreiner, P. R.; Fokin, A. A.; Pascal, R. A.; deMeijere, A., “Many Density Functional Theory Approaches Fail To Give Reliable Large Hydrocarbon Isomer Energy Differences,” Org. Lett. 2006, 8, 3635-3638, DOI: 10.1021/ol0610486

(6) Wodrich, M. D.; Corminboeuf, C.; Schleyer, P. v. R., “Systematic Errors in Computed Alkane Energies Using B3LYP and Other Popular DFT Functionals,” Org. Lett. 2006, 8, 3631-3634, DOI: 10.1021/ol061016i

(7) Zhao, Y.; Schultz, N. E.; Truhlar, D. G., “Design of Density Functionals by Combining the Method of Constraint Satisfaction with Parametrization for Thermochemistry, Thermochemical Kinetics, and Noncovalent Interactions,” J. Chem. Theory Comput. 2006, 2, 364-382, DOI: 10.1021/ct0502763.

(8) Zhao, Y.; Truhlar, D. G., “Assessment of Model Chemistries for Noncovalent Interactions,” J. Chem. Theory Comput. 2006, 2, 1009-1018, DOI: 10.1021/ct060044j.

(9) Wodrich, M. D.; Corminboeuf, C.; Schreiner, P. R.; Fokin, A. A.; Schleyer, P. v. R., “How Accurate Are DFT Treatments of Organic Energies?,” Org. Lett., 2007, 9, 1851-1854, DOI: 10.1021/ol070354w.

InChI

1: InChI=1/C11H10/c1-2-5-7-3(1)4(1)8-6(2)10-9(5)11(7,8)10/h1-10H

2: InChI=1/C12H12/c1-2-4-10-6-8-11-7-5-9(3-1)12(10)11/h1-12H

3: InChI=1/C12H12/c1-2-4-8-11(7-3-1)12-9-5-6-10-12/h1-12H

4: InChI=1/C6H6/c1-4-5(2)6(4)3/h1-3H2

5: InChI=1/C8H10/c1-3-7-5-6-8(7)4-2/h3-4H,1-2,5-6H2

6: InChI=1/C10H10/c1-2-8-5-6-9-4-3-7(1)10(8)9/h1-10H