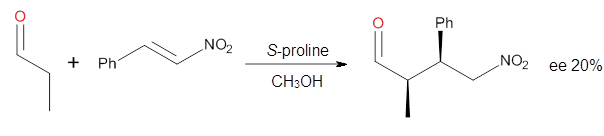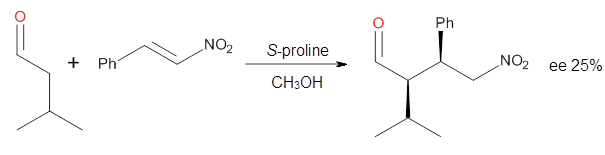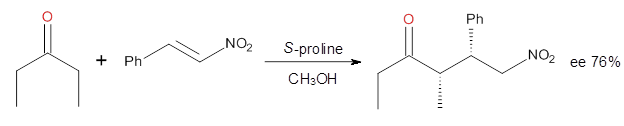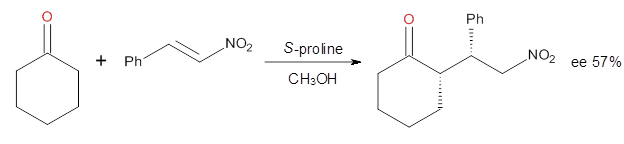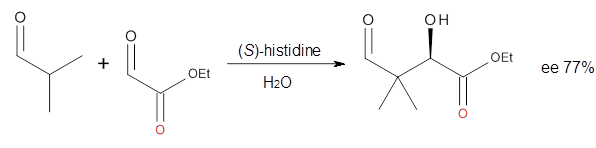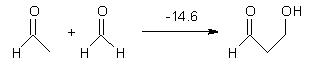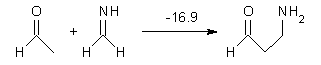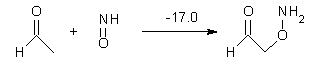Here are a couple of articles describing computational approaches to catalytic enantioselective reactions using variations upon the classic proline-catalyzed aldol reaction of List and Barbas¹ that started the whole parade. I have discussed the major computational papers on that system in my book (Chapter 5.3).

Yang and Wong² investigated the proline-catalyzed nitro-Michael reaction, looking at four examples, two with aldehydes and two with ketones (Reactions 1-4).

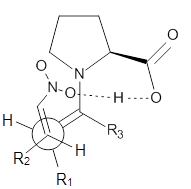
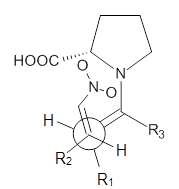
These four reactions were examined atMP2/311+G**//M06-2x/6-31G**, and PCM was also applied. The key element of this study is that they examined two different types of transition states: (a) based on the Houk-List model involving a hydrogen bond and (b) an electrostatic based model with no hydrogen bond. These are sketched in Scheme 1. For each of the reactions 1-4 there are 8 located transition states differing in the orientation of the attack on to the syn or anti enamine.

Scheme 1. TS models

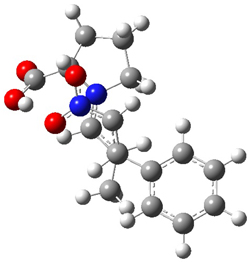
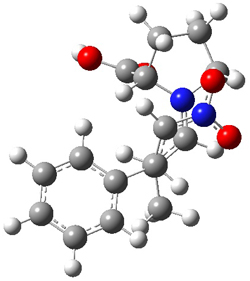
The two lowest energy TS are shown in Figure 1. TS1-β1-RS is the lowest TS and it leads to the major enantiomer. The second lowest TS, TS1-β3-SR, lies 2.9 kJ mol^-1 above the other TS, and it leads to the minor enantiomer. This lowest TS is of the Houk-List type (Model A) while the other TS is of the Model B type. The enthalpies of activation suggest an ee of 54%, in reasonable
agreement with experiment.

TS1-β1-RS

TS1-β1-RS

Figure 1. M06-2x/6-31G** optimized geometries of TS1-β1-RS and TS1-β1-RS.

The computations of the other three reactions are equally good in terms of agreement with experiment, and importantly the computations indicate the reversal of stereoselection between the aldehydes and the ketones. These computations clearly implicate both the Houk-List and the non-hydrogen bonding TSs in the catalyzed Michael additions.

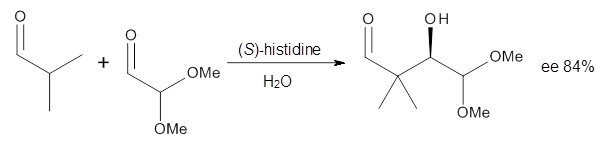
Houk in collaboration with Scheffler and Mahrwald investigate the use of histidine as a catalyst for the asymmetricaldol reaction.³ Examples of the histidine-catalyzed aldol are shown in Reactions 5-7.

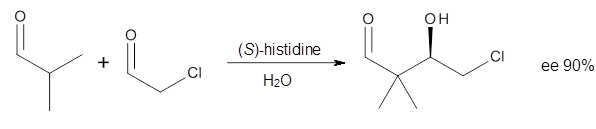
	Reaction 5
	Reaction 6
	Reaction 7

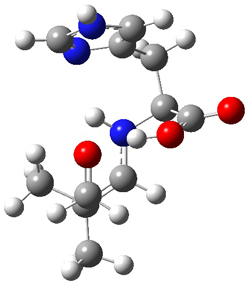
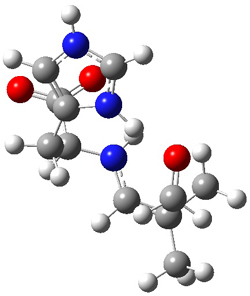
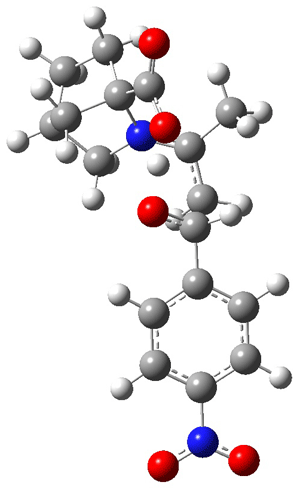
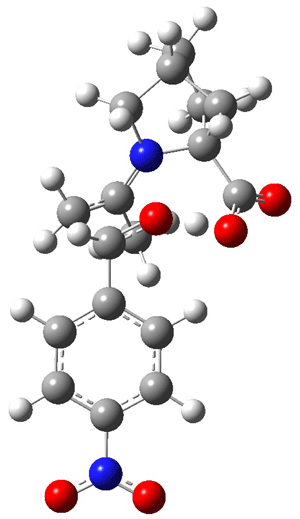
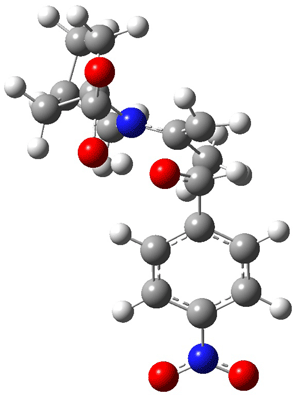
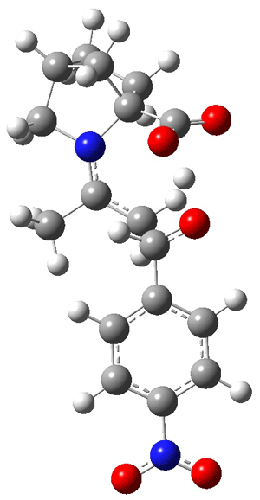
The interesting twist here is whether the imidazole can also be involved in hydrogen bonding to the acceptor carbonyl group, serving the purpose of the carboxylic acid group in the Houk-List TS when proline is the catalyst (Model A). The transition states for these and a few other reactions were computed at M06-2x/6-31+G(d,p) including with the SMD continuum solvent model for water. The two lowest energy TSs for the reaction of isobutyraldehde and formaldehyde are shown in Figure 2; TS1 has the carboxylic acid group as the hydrogen donor while the imidazole is the donor in TS2. Of note is that these two TS are isoenergetic, indicating that both modes of stabilization are at play with histidine as the catalyst.

TS1

TS2

Figure 2. M06-2x/6-31+G(d,p) geometries of the two lowest energy TSs for the reaction of isobutyraldehde and formaldehyde catalyzed by histidine.

The possible TSs for Reactions 5-7 were also located. For example, with Reaction 5, the lowest energy TS involves the imidazole as the hydrogen donor and it leads to the major product. The lowest energy TS that leads to the minor product involves the carboxylic acid as the donor. The computed ee’s for Reactions 5-7 are in very good, if not excellent, agreement with the experimental values. The study should spur further activity in which one might tune the stereoselectivity by using catalysts with multiple binding opportunities.

References

(1) List, B.; Lerner, R. A.; Barbas, C. F., III; "Proline-Catalyzed Direct Asymmetric Aldol Reactions," J. Am. Chem. Soc., 2000, 122, 2395-2396, DOI: 10.1021/ja994280y.

(2) Yang, H.; Wong, M. W. "(S)-Proline-catalyzed nitro-Michael reactions: towards a better understanding of the catalytic mechanism and enantioselectivity," Org. Biomol. Chem.,
2012, 10, 3229-3235, DOI: 10.1039/C2OB06993H

(3) Lam, Y.-h.; Houk, K. N.; Scheffler, U.; Mahrwald, R. "Stereoselectivities of Histidine-Catalyzed Asymmetric Aldol Additions and Contrasts with Proline Catalysis: A Quantum Mechanical Analysis," J. Am. Chem. Soc. 2012, 134, 6286-6295, DOI: 10.1021/ja2118392

The proline-catalyzed aldol reaction is discussed in Chapter 5.3 of my book. This is an area of continued research and the recent paper of Sharma and Sunoj addresses an alternative mechanism involving oxazolidinone.¹ They examine the proline-catalyzed aldol self-condensation of propanal with B3LYP/6-31+G** and MP2/6-31+G** computations. This reaction is found to proceed² with 4:1 anti:syn diastereoselectivity.

An oxazolidinone intermediate has been observed in proline-catalyzed aldol condensations. This intermediate is proposed to come about via Path b, whereas the generally accepted mechanism put forth by Houk and List, discussed in my book, follows Path a. Sharma and Sunoj find that the oxazolidinone 7 is lower in energy than the enamine 4, and its barrier for ring opening back to 3 is large. Thus, it is not unreasonable that it is the observed intermediate.

Gas phase computations of the reaction of 4 to 5 predict a 99% ee and an anti:syn ratio of about 5:1, in nice agreement with experiment. However, incorporation of solvent reduces the ration to 2:1, and the MP2 computations give a ratio of 1.2:1, in even worse agreement with experiment. However, the major predicted product has the same absolute configuration as the observed product.

The other mechanism is examined in the key step 8 to 9. Here all computations predict that syn addition is favored over anti addition and the enantiomer of the experimentally observed product is predicted to be formed. In addition, intermediate 9 and the TSs leading to it are much higher in energy than intermediate 5 and the TSs associated with its formation. Thus, the oxazolidinone addition mechanism is discounted.

References

(1) Sharma, A.; Sunoj, R., "Enamine versus Oxazolidinone: What Controls Stereoselectivity in Proline-Catalyzed Asymmetric Aldol Reactions?," Angew. Chem. Int. Ed., 2010, 49, 6373-6377, DOI: 10.1002/anie.201001588

(2) Northrup, A. B.; MacMillan, D. W. C., "The First Direct and Enantioselective Cross-Aldol Reaction of Aldehydes," J. Am. Chem. Soc., 2002, 124, 6798-6799, DOI: 10.1021/ja0262378

Houk has performed a very nice examination of the performance of some density functionals.¹ He takes a quite different approach than what was proposed by Grimme – the “mindless” benchmarking² using random molecules (see this post). Rather, Houk examined a series of simple aldol, Mannich and α-aminoxylation reactions, comparing their reaction energies predicted with DFT against that predicted with CBQ-QB3. The idea here is to benchmark DFT performance for simple reactions of specific interest to organic chemists. These reactions are of notable current interest due their involvement in organocatalytic enantioselective chemistry (see my posts on the aldol, Mannich, and Hajos-Parrish-Eder-Sauer-Wiechert reaction). Examples of the reactions studied (along with their enthalpies at CBS-QB3) are Reaction 1-3.

For the four simple aldol reactions and four simple Mannich reactions, PBE1PBE,
mPW1PW91 and MO6-2X all provided reaction enthalpies with errors of about 2 kcal mol^-1. The much maligned B3LYP functional, along with B3PW91 and B1B95 gave energies with significant larger errors. For the three α-aminoxylation reactions, the errors were better with B3PW91 and B1B95 than with PBE1PBE or MO6-2X. Once again, it appears that one is faced with finding the right functional for the reaction under consideration!

Of particular interest is the decomposition of these reactions into related isogyric, isodesmic
and homdesmic reactions. So for example Reaction 1 can be decomposed into Reactions 4-7 as shown in Scheme 1. (The careful reader might note that these decomposition reactions are isodesmic and homodesmotic and hyperhomodesmotic reactions.) The errors for Reactions 4-7 are typically greater than 4 kcal mol^-1 using B3LYP or B3PW91, and even with MO6-2X the errors are about 2 kcal mol^-1.

Scheme 1.

Houk also points out that Reactions 4, 8 and 9 (Scheme 2) focus on having similar bond changes as in Reactions 1-3. And it’s here that the results are most disappointing. The errors produced by all of the functionals for Reactions 4,8 and 9 are typically greater than 2 kcal mol^-1, and even MO2-6x can be in error by as much as 5 kcal mol^-1. It appears that the reasonable performance of the density functionals for the “real world” aldol and Mannich reactions relies on fortuitous cancellation of errors in the underlying reactions. Houk calls for the development of new functionals designed to deal with fundamental simple bond changing reactions, like the ones in Scheme 2.

Scheme 2

References

(1) Wheeler, S. E.; Moran, A.; Pieniazek, S. N.; Houk, K. N., "Accurate Reaction Enthalpies and Sources of Error in DFT Thermochemistry for Aldol, Mannich, and α-Aminoxylation Reactions," J. Phys. Chem. A 2009, 113, 10376-10384, DOI: 10.1021/jp9058565

(2) Korth, M.; Grimme, S., ""Mindless" DFT Benchmarking," J. Chem. Theory Comput. 2009, 5, 993–1003, DOI: 10.1021/ct800511q

In Chapter 5.3.2, I extensively discuss the organocatalyzed aldol reaction. Barbas and List have pioneered the use of proline to catalyze this reaction, and Houk has performed a series of computational studies to discern the mechanism. The mechanism is essentially the attack of the enamine on the carbonyl with concomitant proton transfer from the carboxylic acid to the forming oxyanion.

Shininisha and Sunoj have examined a number of bicyclic analogues of proline (1-11) as catalysts of the aldol reaction.¹ They computed the activation energies for the reaction of the enamine derived from acetone with p-nitrobenzaldehyde with the various catalysts. All computations were performed at B3LYP/6-311+G**//B3LYP/6-31G* with the solvent effects modeled using CPCM.

As Houk has demonstrated, there are four possible transition states: the attack can come to either the re or si face of the aldehyde and either the syn or anti enamine can be the reactant. The four transition states for the reaction of 8 are shown in Figure 1. These TSs are representative of all of the transition states involving the different catalysts, including proline itself. These TS are characterized by proton transfer accompanying the C-C bond formation. Their relative energies can be interpreted in terms of the distortions about the enamine double bond (the more planar, the lower the energy) and the arrangement of the carboxylic acid and the incipient oxyanion. These arguments were made by Houk and are described in my book.

8-anti-re 0.0	8-anti-si 2.12
8-syn-re 8.15	8-syn-si 7.28

Figure 1. B3LYP/6-311+G**//B3LYP/6-31G* optimized structures and relative energies (kcal/mol) of the transition states of the enamine derived from acetone and 8 with p-nitrobenzaldehyde¹

The enantiomeric excess predicted by the computations for the aldol reaction using the 11 different bicyclic catalysts is presented in Table 1. All of the catalysts except 11 give high enantiomeric excess, with a number of them predicted to produce an ee above 90%. The authors conclude that these catalysts are worth exploring, since they are predicted to perform better than proline (which has a predicted ee of 75%).

Table 1. Predicted ee for the reaction of the enamine derived
from acetone and catalyst with p-nitrobenzaldehyde.

References

(1) Shinisha, C. B.; Sunoj, R. B., "Bicyclic Proline Analogues as Organocatalysts for Stereoselective Aldol Reactions: an in silico DFT Study," Org. Biomol. Chem., 2007, 5, 1287-1294, DOI: 10.1039/b701688c.

InChIs

1: InChI=1/C8H13NO2/c1-5-4-6-2-3-8(5,9-6)7(10)11/h5-6,9H,2-4H2,1H3,(H,10,11)

2: InChI=1/C8H13NO2/c1-5-4-8(7(10)11)3-2-6(5)9-8/h5-6,9H,2-4H2,1H3,(H,10,11)

3: InChI=1/C6H9NO2/c8-5(9)6-2-1-4(3-6)7-6/h4,7H,1-3H2,(H,8,9)

4: InChI=1/C6H9NO3/c8-5(9)6-2-1-4(7-6)10-3-6/h4

5: InChI=1/C5H7NO3/c7-4(8)5-1-3(6-5)9-2-5/h3,6H,1-2H2,(H,7,8)

6: InChI=1/C6H9NO2S/c8-5(9)6-2-1-4(7-6)10-3-6/h4,7H,1-3H2,(H,8,9)

7: InChI=1/C5H7NO2S/c7-4(8)5-1-3(6-5)9-2-5/h3,6H,1-2H2,(H,7,8)

8: InChI=1/C7H11NO2/c9-6(10)7-2-1-5(3-7)4-8-7/h5,8H,1-4H2,(H,9,10)

9: InChI=1/C7H11NO2/c9-7(10)6-4-1-2-5(3-4)8-6/h4-6,8H,1-3H2,(H,9,10)

10: InChI=1/C6H9NO2/c8-6(9)5-3-1-4(2-3)7-5/h3-5,7H,1-2H2,(H,8,9)

11: InChI=1/C6H9NO2/c8-6(9)5-3-1-4(5)7-2-3/h3-5,7H,1-2H2,(H,8,9)