Well, here’s my vote for paper of the year (at least so far!). It is work from Barry Carpenter’s lab¹ and pertains to many topics discussed in my book, including pericyclic and psuedopericylic reactions, non-statistical dynamics, and the use of high-level computations to help understand confusing experimental results. The paper is in an interesting read – and not just for the great science. It is told as a story, recounting the experiments and interpretation as they took place in chronological order with a surprising and critical contribution made from a referee!

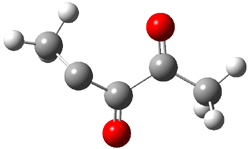
The story begins with Carpenter’s continuing interest in unusual dynamic effects and the supposition that non-statistical dynamics might be observed in the rearrangements of carbenes. So, they took on the Wolff rearrangement, specifically the rearrangement of 3 into 4. Using labeled starting material 1, one should observe equal amounts of 4a and 4b if normal statistical dynamics is occurring (Scheme 1).

Scheme 1.

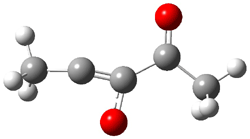
In fact, the ratio of products is not unity, but rather 4a:4b = 1:4.5. But the excess of 4b could be the result of another parallel rearrangement, 2 to 5 to 4b (Scheme 2).

Scheme 2.

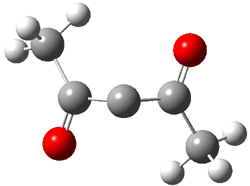
To try to distinguish whether 5 is intervening, they carried out the photolysis of a different labeled version of 1 (namely 1’). The product distribution of the products is shown in Sheme 3. It appears that the reaction through 5 dominates, but the ratio of products that come from 3 still shows non-statistical behavior.

Scheme 3.

CCSD(T) computation suggested that 5 is higher in energy than 3, and this does not help understand the experiments. At this point, Carpenter decided to write up the work as a communication, with the main point that non-statistical dynamics were occurring.

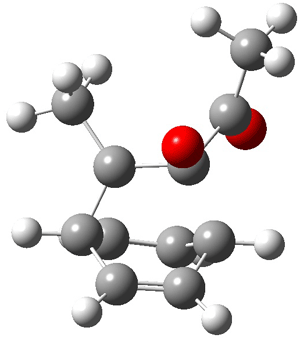
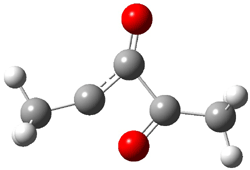
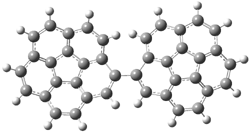
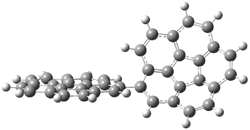
Now here an unusual event took place that offers up hope that the peer-review system still works! A referee, later identified as Dan Singleton, offered an alternative mechanism for the production of 5. Shown in Scheme 4 is the novel pseudopericylic reaction that leads from 1 directly to 5. In fact, the transition state for this pseudopericyclic reaction is 19.0 kcal mol^-1 lower in energy than the transition state for the retro-Diels-Alder reaction of Scheme 1 (computed at MPWB1K/ 6-31+G(d,p), and this pseudopericyclic TS is shown in Figure 1).

Scheme 4.

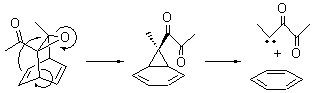
Figure 1. MPWB1K/6-31+G(d,p) optimized geometry of the transition state for the pseudopericyclic reaction shown in Scheme 4.¹

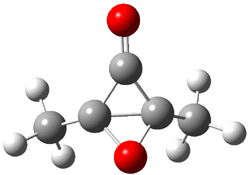
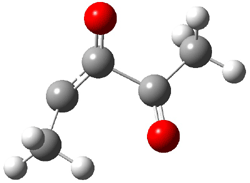
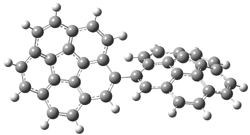
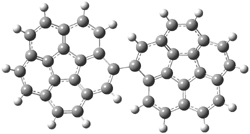
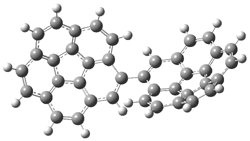
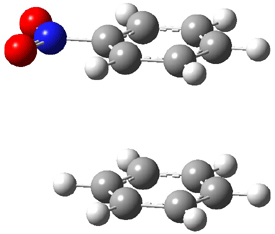
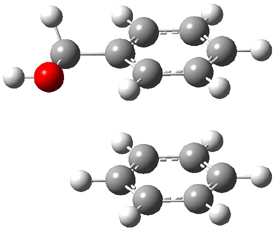
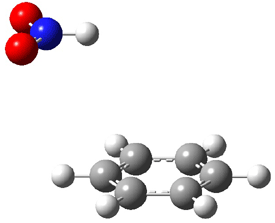
The revised mechanism was then modified to include the additional complication of the formation of 6, and is shown in Scheme 5, along with their relative CCSD(T) energies. The CCSD(T)/cc-pVTZ//CCSD/cc-pVTZ optimized geometries of the critical points of Scheme 5 are drawn in Figure 2.

Scheme 5.

5
TS 5 → 3	3
TS 5 → 6	6
TS 5 → 4	4

Figure 2. CCSD/cc-pVTZ optimized geometries.¹

Any non-statistical effect would occur in the transition from 5 to 3. A direct dynamics trajectory analysis was performed starting in the neighborhood of this TS using three different functionals to generate the potential energy surface. Though only 100 trajectories were computed, the results with all three functionals are similar. About 2/3rds of these trajectories led to 3 followed by the shift of the C₅ methyl group. Another 15% led to 3 and then the C₁ methyl shifted. This MD simulation supports the non-statistical Wolff rearrangement, with a clear preference for the C₅ shift, consistent with experiment. A larger MD study is underway and will hopefully shed additional insight onto this fascinating reaction.

References

(1) Litovitz, A. E.; Keresztes, I.; Carpenter, B. K., "Evidence for Nonstatistical Dynamics in the Wolff Rearrangement of a Carbene," J. Am. Chem. Soc., 2008, 130, 12085-12094, DOI: 10.1021/ja803230a.

InChIs

3: InChI=1/C5H6O2/c1-4(6)3-5(2)7/h1-2H3
InChIKey = IGYQBMPIQGLNRU-UHFFFAOYAO

4: InChI=1/C5H6O2/c1-4(3-6)5(2)7/h1-2H3
InChIKey = ABVJXABNYINQLN-UHFFFAOYAA

5: InChI=1/C5H6O2/c1-3-5(7)4(2)6/h1-2H3
InChIKey = FJJXVDYICOYKRN-UHFFFAOYAD

6: InChI=1/C5H6O2/c1-4-3(6)5(4,2)7-4/h1-2H3
InChIKey = CAMBQRQJZBTNNS-UHFFFAOYAB

Consider bicorannulenyl 1. Each corranulene unit is a bowl and each is chiral due to being monosubstituted. Additional chirality is due to the arrangement of the bowls along the C₁-C_1’ bond, the bond where the two rings join. So both rotation about the C₁-C_1’ bond and bowl inversion will change the local chirality (Scheme 1 distinguishes these two processes.) One might anticipate that the stereodynamics of 1 will be complicated!

Scheme 1

Rabinovitz, Scott, Shenhar and their groups have tackled the stereodynamics of 1.¹ (This is a very nice joint experimental and theoretical study and I wonder why it did not appear in JACS.) At room temperature and above, one observes a single set of signals, a singlet and eight doublets, in the ¹H NMR. Below 200 K, there are three sets of signals, evidently from three different diastereomers.

Each ring can have either P or M symmetry. The authors designate conformations using these symbols for each ring along with the value of the torsion angle about the C₁-C_1’ bond. So, for example, a PP isomer is the enantiomer of the MM conformer when their dihedral angles are of opposite sign.

DFT computations help make sense of these results. PBE0/6-31G* computations reveal all local minima and rotational and inversion transition states of 1. The lowest (free) energy structure is PP₄₄ (see Figure 1). A very small barrier separates it from PP₁₁₁; this barrier is related to loss of conjugation between the two rings. Further rotation must cross a much larger barrier (nearly 17 and 20 kcal mol^-1). These barriers result from the interaction of the C₂ hydrogen of one ring with either the C_2’ or C_10’ hydrogen, similar to the rotational barrier in 1,1’-binaphthyl. However, the barrier is lower in 1 than in 1,1’-binaphthyl due to the non-planar nature of 1 that allows the protons to be farther apart in the TS. Once over these large barriers, two local minima, PP_-45 and PP_-137, separated by a small barrier are again found.

PP44 0.0	PP-28 19.80	PP-45 3.38
PP111 1.54	PP166 16.76	PP-137 0.14

Figure 1. PBE0/6-31G* optimized geometries and relative free energies (kcal mol^-1) of the PP local minima (PP₄₄, PP₁₁₁, PP_-45, and PP_-137) and rotational transition states.¹

The lowest energy bowl inversion transition state (P₄₉) lies 9.6 kcal mole^-1 above PP₄₄. It is shown in Figure 2. The bowl inversion barrier is comparable to that found in other substituted corannulenes,² which are typically about 9-12 kcal mol^-1).

P49 9.58

Figure 2. PBE0/6-31G* optimized geometry and relative free energy of the lowest energy bowl inversion transition state.¹

Interestingly, it is easier to invert the bowl than to rotate about the C₁-C_1’ bond. And this offers an explanation for the experimental ¹H NMR behavior. At low temperature, crossing the low rotational barriers associated with loss of conjugation occurs. So, using the examples from Figure 1, PP₄₄ and PP₁₁₁ appear as a single time-averaged signal in the NMR. This leads to three pairs of enantiomers (S.PP/R.PP, S.MM/R.PP, and S.PM/R.MP), giving rise to the three sets of NMR signals.

References

(1) Eisenberg, D.; Filatov, A. S.; Jackson, E. A.; Rabinovitz, M.; Petrukhina, M. A.; Scott, L. T.; Shenhar, R., "Bicorannulenyl: Stereochemistry of a C40H18 Biaryl Composed of Two Chiral Bowls," J. Am. Chem. Soc. 2008, 73, 6073-6078, DOI: 10.1021/jo800359z.

(2) Wu, Y. T.; Siegel, J. S., "Aromatic Molecular-Bowl Hydrocarbons: Synthetic Derivatives, Their Structures, and Physical Properties," Chem. Rev. 2006, 106, 4843-4867, DOI: 10.1021/cr050554q.

InChIs

1: InChIKey = XZISQKATUXKXQW-UHFFFAOYAG

Ken Houk has produced a very nice minireview on bifurcations in organic reactions.¹ This article is a great introduction to a topic that has broad implication for mechanistic concepts. Bifurcations result when a valley-ridge inflection point occurs on or near the intrinsic reaction coordinate. This inflection point allows trajectories to split into neighboring basins (to proceed to different products) without crossing a second transition state. In the examples discussed, the reactant crosses a single transition state and then leads to two different products. This is the so-called “two-step no intermediate” process.

I discuss the implications of these kinds of potential energy surfaces, and other ones of a pathological nature, in the last chapter of my book. Very interesting reaction dynamics often are the result, leading to a mechanistic understanding far from the ordinary!

References

(1) Ess, D. H.; Wheeler, S. E.; Iafe, R. G.; Xu, L.; Çelebi-Ölçüm, N.; Houk, K. N., "Bifurcations on Potential Energy Surfaces of Organic Reactions," Angew. Chem. Int. Ed. 2008, DOI: 10.1002/anie.200800918

An alternative take on the nature of the interaction in π-stacking is offered by Wheeler and Houk.¹ They start by examining the binding between benzene and a series of 24 substituted benzenes. Two representative dimmers are shown in Figure 1, where the substituent is NO₂ or CH₂OH. As was noted in a number of previous studies,^2-6 the binding with any substituted benzene is stronger than the parent benzene dimer. Nonetheless, Wheeler and Houk point out that the binding energy has a reasonable correlation with σ_m. It appears that the benzene dimer itself is the outlier; the binding energy when the substituent is CH₂OH, whose σ_m value is zero, is bound more tightly than the benzene dimer. They conclude that there is a dispersive interaction between any substituent and the other benzene ring.

(a)	(b)
(c)	(d)

Figure 1. MO5-2X/6-31+G(d) optimized geometries of (a) C₆H₆-C₆H₅NO₂, (b) C₆H₆-C₆H₅CH₂OH, (c) C₆H₆-HNO₂, and (d) C₆H₆-HCH₂OH.¹

They next constructed an admittedly very crude model system whereby the substituted benzene C₆H₅X is replaced by HX; the corresponding models are also shown in Figure 1. The binding energies of these model dimmers correlates very well with the real dimmers, with r = 0.91. Rather than involving the interaction of the π-electrons, the origin of the enhanced binding in aromatic dimers involves electrostatic interactions of the substituent with the other aromatic ring – effectively the quadrupole of the unsubstituted ring interacts with the dipoles of the substituent and its ring system. In addition, the inherent dispersive interaction increase the binding.

References

(1) Wheeler, S. E.; Houk, K. N., "Substituent Effects in the Benzene Dimer are Due to Direct Interactions of the Substituents with the Unsubstituted Benzene," J. Am. Chem. Soc., 2008, 130, 10854-10855, DOI: 10.1021/ja802849j.

(2) Sinnokrot, M. O.; Sherrill, C. D., "Unexpected Substituent Effects in Face-to-Face π-Stacking Interactions," J. Phys. Chem. A, 2003, 107, 8377-8379, DOI: 10.1021/jp030880e.

(3) Sinnokrot, M. O.; Sherrill, C. D., "Substituent Effects in π-&pi Interactions: Sandwich and T-Shaped Configurations," J. Am. Chem. Soc., 2004, 126, 7690-7697, DOI: 10.1021/ja049434a.

(4) Sinnokrot, M. O.; Sherrill, C. D., "Highly Accurate Coupled Cluster Potential Energy Curves for the Benzene Dimer: Sandwich, T-Shaped, and Parallel-Displaced Configurations," J. Phys. Chem. A, 2004, 108, 10200-10207, DOI: 10.1021/jp0469517

(5) Lee, E. C.; Kim, D.; Jurecka, P.; Tarakeshwar, P.; Hobza, P.; Kim, K. S., "Understanding of Assembly Phenomena by Aromatic-Aromatic Interactions: Benzene Dimer and the Substituted Systems," J. Phys. Chem. A 2007, 111, 3446-3457, DOI: 10.1021/jp068635t.

(6) Grimme, S.; Antony, J.; Schwabe, T.; Mück-Lichtenfeld, C., "Density functional theory with dispersion corrections for supramolecular structures, aggregates, and complexes of
(bio)organic molecules," Org. Biomol. Chem. 2007, 741-758, DOI: 10.1039/b615319b

I have an immediate opening in my group for a post-doctoral associate. The position involves computational approaches to a variety of problems, including nucleophilic substitution at heteroatoms, solvent effects, and host-guest chemistry. The candidate must have some experience with computational chemistry, especially with any one of the major ab initio programs (like Gaussian, or Gamess or NWChem, etc.).

If you are interested in the position, please see the description here.

Angewandte Chemie has published a rather unusual short article – an appeal by Roald Hoffmann, Paul Schleyer and Fritz Schaefer (the latter two were interviewed in my book!) to use “more realism, please!”¹

These noted computational chemists suggest that we all have been sloppy in the language we use in describing our computations. They first take on the term “stable”, and rightfully point out that this is a very contextual term – stable where? on my desktop? In a 1M aqueous solution? Inside a helium glove box? Inside a mass spectrometer? In an interstellar cloud? Stable for how long? Indefinitely? For a day? For a day in the humid weather of San Antonio? Or a day inside a cold refrigerator? Or how about inside a Ne matrix? Or for the time it takes to run a picosecond laser experiment?

The authors offer up the terms “viable” and “fleeting” as reasonable alternatives and proscribe a protocol for meeting the condition of “viable” – and I must note that this protocol is very demanding, likely beyond the computational abilities of many labs and certainly beyond what can be done for a reasonably large molecule.

They also take on the uncertainty of computed results, pointing out the likely largely overlooked irreproducibility of many DFT results, due to size difference of the computed grids, difference in implementation of the supposedly same functional, etc. They conclude with a discussion of how many significant figures one should employ.

None of this is earth-shattering, and most is really well-known yet often neglected or overlooked. In another interesting publication treat in this issue, four referee reports of the article are reproduced. The first, by Gernot Frenking,² argues exactly this point – that the lack of new information, and the sort of whimsical literary approach make the article unacceptable for publication. The other three referees disagree,^3-5 and note that though the article is not novel, the authors forcefully remind us that better behaviors should be put into practice.

The article is a nice reminder that careful studies should be carefully reported. (And both the authors of the article and the referees note that these same comments apply to our experimental colleagues, too.)

References

(1) Hoffmann, R.; Schleyer, P. v. R.; Schaefer III, H. F., “Predicting Molecules – More Realism, Please!,” Angew. Chem. Int. Ed., 2008, 47, 7164-7167, DOI: 10.1002/anie.200801206.

(2) Frenking, G., “No Important Suggestions,” Angew. Chem. Int. Ed. 2008, 47, 7168-7169, doi: 10.1002/anie.200802500.

(3) Koch, W., “Excellent, Valuable, and Entertaining,” Angew. Chem. Int. Ed., 2008, 47, 7170, DOI: 10.1002/anie.200802996.

(4) Reiher, M., “Important for the Definition of Terminology in Computational Chemistry,” Angew. Chem. Int. Ed., 2008, 48, 7171, DOI: 10.1002/anie.200802506.

(5) Bickelhaupt, F. M., “Attractive and Convincing,” Angew. Chem. Int. Ed., 2008, 47, 7172, DOI: 10.1002/anie.200802330.

Schaefer and Allen have applied their focal point method to the question of the benzylic effect in the S_N2 reaction.¹ S_N2 reactions are accelerated when the attack occurs at the benzylic carbon, a well-known phenomenon yet the reason for this remains unclear. The standard textbook-like argument has been that the negative charge built up in the S_N2 transition state can be delocalized into the phenyl ring. However, solution phase Hammett studies are often U-shaped, indicating that both electron donating and withdrawing group accelerate the substitution reaction. (This is usually argued as indicative of a mechanism change from S_N2 to S_N1.)

The focal point method involves a series of very large computations where both basis set size and degree of electron correlation are systematically increased, allowing for an extrapolation to essentially infinite basis set and complete correlation energy. The energy of the transition state (relative to separated reactants) for four simple S_N2 reactions evaluated with the focal point method are listed in Table 1. The barrier for the benzylic substitutions is lower than for the methyl cases, indicative of the benzylic effect.

Table 1. Energy (kcal mol^-1) of the transition state relative to reactants.¹

To answer the question of why the benzylic substitution reactions are faster, they examined the charge distribution evaluated at B3LYP/DZP++. As seen in Table 1, this method does not accurately reproduce the activation barriers, but the errors are not terrible, and the trends are correct.

In Figure 1 are the geometries of the transition states for the reaction of fluoride with methylflouride or benzylfluoride. The NBO atomic charges show that the phenyl ring acquired very little negative charge at the transition state. Rather, the electric potential at the carbon under attack is much more revealing. The potential is significantly more positive for the benzylic carbon than the methyl carbon in both the reactant and transition states.

VC = -405.156 V	VC = -404.379 V

Figure 1. MP2/DZP++ transition states for the reaction of fluoride with methylfluoride and benzylflouride. NBO charges on F and C and the electrostatic potential in Volts.¹

They next examined the reaction of fluoride with a series of para-substituted benzylfluorides. The relation between the Hammet σ constants and the activation energy is fair (r = 0.971). But the relation between the electrostatic potential at the benzylic carbon (in either the reactant or transition state) with the activation energy is excellent (r = 0.994 or 0.998). Thus, they argue that it is the increased electrostatic potential at the benzylic carbon that accounts for the increased rate of the S_N2 reaction.

References

(1) Galabov, B.; Nikolova, V.; Wilke, J. J.; Schaefer III, H. F.; Allen, W. D., "Origin of the S_N2 Benzylic Effect," J. Am. Chem. Soc., 2008, 130, 9887-9896, DOI: 10.1021/ja802246y.