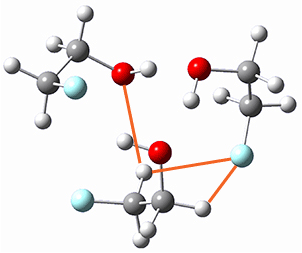
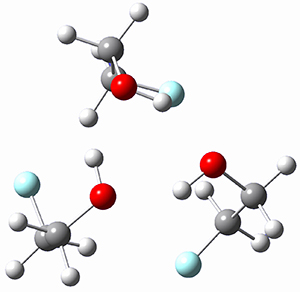
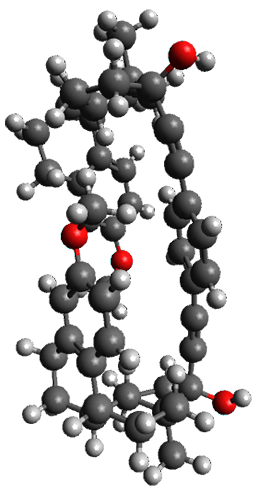
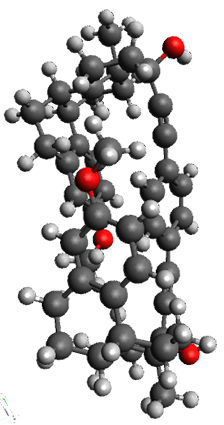
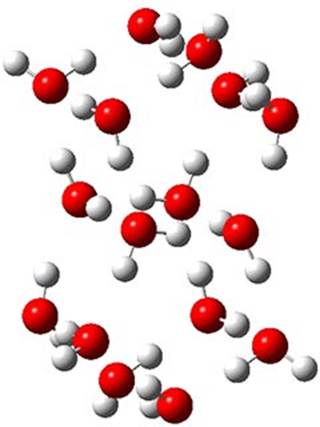
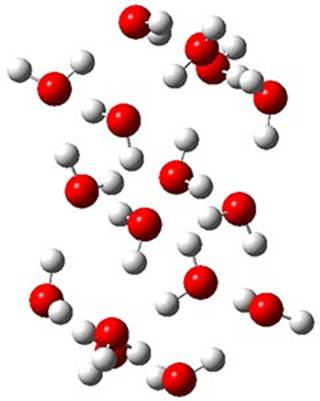
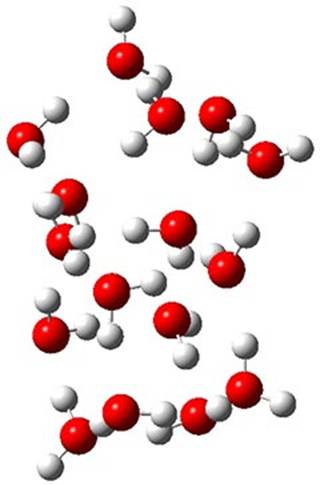
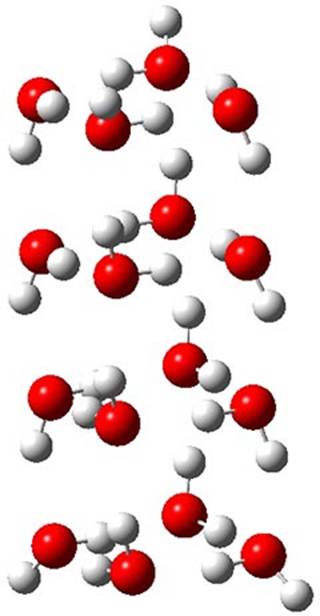
Here is another fine example of the power of combining experiment and computation. Xu and co-worker has applied the FT microwave technique, which has been used in conjunction with computation by the Alonso group (especially) as described in these posts, to the trimer of 2-fluoroethanol.¹ They computed a number of trimer structures at MP2/6-311++G(2d,p) in an attempt to match up the computed spectroscopic constants with the experimental constants. The two lowest energy structures are shown in Figure 1. The second lowest energy structure has nice symmetry, but it does not match up well with the experimental spectra. However, the lowest energy structure is in very good agreement with the experiments.

(0.0)

(4.15)

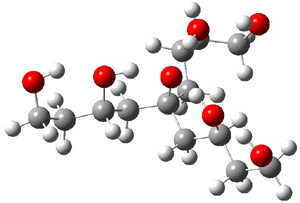
Table 1. MP2/6-311++G(2d,p) optimized structures and relative energies (kJ mol^-1) of the two lowest energy structures of the trimer of 2-fluoroethanol. The added orange lines in the lowest energy structure denote the bifurcated hydrogen bonds identified by QTAIM.

Of particular note is that topological electron density analysis (also known as quantum theoretical atoms in a molecule, QTAIM) of the wavefunction of the lowest energy structure of the trimer identifies two hydrogen bond bifurcations. The authors suggest that these additional interactions are responsible, in part, for the stability of this lowest energy structure.

References

(1) Thomas, J.; Liu, X.; Jäger, W.; Xu, Y. "Unusual H-Bond Topology and Bifurcated H-bonds in the 2-Fluoroethanol Trimer," Angew. Chem. Int. Ed. 2015, 54, 11711-11715, DOI: 10.1002/anie.201505934.

InChIs

2-fluoroethanol: InChI=1S/C2H5FO/c3-1-2-4/h4H,1-2H2, InChIKey=GGDYAKVUZMZKRV-UHFFFAOYSA-N

Molecular rotors remain a fascinating topic – the idea of creating a miniature motor just seems to capture the imagination of scientists. Garcia-Garibay and his group have synthesized the interesting rotor 1, and in collaboration with the Houk group, they have utilized computations to help understand the dynamics of this rotor.¹

The x-ray structure of this compound, shown in Figure 1, displays two close interactions of a hydrogen on the central phenyl ring with the face of one of the steroidal phenyl rings. Rotation of the central phenyl ring is expected to then “turn off” one or both of these C-H^…π interactions. The authors argue this as a competition between the molecule sampling an enthalpic region, where the molecule has one or two favorable C-H^…π interactions, and the large entropic region where these C-H^…π interactions do not occur, but this space is expected to have a large quantity of energetically similar conformations.

x-ray
1a	1b

Figure 1. X-ray and M06-2x/6-31G(d) optimized structures of 1.

Variable temperature NMR finds the central phenyl hydrogen with a chemical shift of 6.55ppm at 295 K but at 6.32 ppm at 222 K. This suggest as freezing of the conformations at low temperature favoring those conformations possessing the internal C-H^…π interactions. M06-2X/6-31G(d) optimization finds two low-energy conformations with a single C-H^…π interaction. These are shown in Figure 1. No competing conformation was found to have two such interactions. Computations of the chemical shifts of these conformations show the upfield shift of the central phenyl hydrogens. Fitting these chemical shifts to the temperature data gives ΔH = -1.74 kcal mol^-1, ΔS = -5.12 esu and ΔG = -0.21 kcal mol^-1 for the enthalpic region to entropic region transition.

References

(1) Pérez-Estrada, S.; Rodrı́guez-Molina, B.; Xiao, L.; Santillan, R.; Jiménez-Osés, G.; Houk, K. N.; Garcia-Garibay, M. A. "Thermodynamic Evaluation of Aromatic CH/π Interactions and Rotational Entropy in a Molecular Rotor," J. Am. Chem. Soc. 2015, 137, 2175-2178, DOI: 10.1021/ja512053t.

InChIs

1: InChI=1S/C48H54O4/c1-45-23-19-39-37-15-11-35(51-3)29-33(37)9-13-41(39)43(45)21-27-47(45,49)25-17-31-5-7-32(8-6-31)18-26-48(50)28-22-44-42-14-10-34-30-36(52-4)12-16-38(34)40(42)20-24-46(44,48)2/h5-8,11-12,15-16,29-30,39-44,49-50H,9-10,13-14,19-24,27-28H2,1-4H3
InChIKey=CXZHCTLIHKZRMW-UHFFFAOYSA-N

One of the more controversial components of Bader’s Atoms-In-Molecules (AIM) theory is the contention that there is a one-to-one correspondence between the existence of a bond critical point and the existence of a chemical bond. I discuss this matter in my book and also in these posts (1 and 2). Lane and co-workers now examine this relationship with regard to hydrogen bonds.¹

They examine the topological structure of the electron density of the series 1,2-ethanediol 1, 1,3-propanediol 2, and 1,3-butanediol 3. They find a bond critical point (bcp) between the hydrogen of one hydroxyl group and the oxygen of the second hydroxyl group for the two large compounds 2 and 3. This forms a ring, and a ring critical point is located as well. However, for 1 they find no bond critical point associated with what might be the intramolecular hydrogen bond in 1. For all three diols, the OH stretching frequencies are diminished relative to monoalcohols. So geometrically and spectroscopically there appears to be a hydrogen bond, but rigorous application of Bader’s notion of bonding says that there is no “bond” in 1.

Lane and coworkers go on to show that the electron density in the three diols is really topologically identical, just differing in a matter of degree. They conclude that the existence of a bond critical point should not be the sole arbiter of bonding, but one of the criteria that can be utilized to assess bonding.

While I am not at all in conflict with this conclusion, the paper contains some issues that need be addressed. First off, “bonding” is not a concept of either-or, rather there is a continuum of bonding. Hydrogen bonding should not at all be confused with covalent or ionic bonding – it is dramatically weaker and so one might consider whether the bcp criteria is applicable at all. The authors really fall into this trap stating “… the absence of a BCP should not necessarily be considered evidence as to the absence of a chemical bond (emphasis mine).” Do we want to consider a hydrogen bond as a chemical bond?

I think the key element overlooked in this study is the strength of the “hydrogen bond”. While not determined in the study, undoubtedly the hydrogen bond strength increases in the order 1 < 2 < 3. What is really to be gained by arguing there is or is not a “hydrogen bond” in all or some of these three molecules? The ring-like conformation is the lowest energy conformation for all three. This is driven by some electrostatic attraction between the OH dipole of one hydroxyl group for the dipole of the second hydroxyl group. When do we want to call this attraction a hydrogen bond? What do we gain by not doing so for all three? If we understand that there is an energy continuum of hydrogen bonding, from weak to weaker, doesn’t that provide enough of a model to interpret and predict chemical structure and behavior?

References

(1) Lane, J. R.; Contreras-García, J.; Piquemal, J.-P.; Miller, B. J.; Kjaergaard, H. G. J. Chem. Theor. Comput. 2013, 9, 3263-3266, DOI: DOI: 10.1021/ct400420r.

InChIs

1: InChI=1S/C2H6O2/c3-1-2-4/h3-4H,1-2H2
InChIKey=>LYCAIKOWRPUZTN-UHFFFAOYSA-N

2: InChI=1S/C3H8O2/c4-2-1-3-5/h4-5H,1-3H2
InChIKey=YPFDHNVEDLHUCE-UHFFFAOYSA-N

3: InChI=1S/C4H10O2/c5-3-1-2-4-6/h5-6H,1-4H2
InChIKey=WERYXYBDKMZEQL-UHFFFAOYSA-N

Truhlar has made a comparison of binding energies and relative energies of five (H₂O)₁₆ clusters.¹ While technically not organic chemistry, this paper is of interest to the readership of this blog as it compares a very large collection of density functionals on a problem that involves extensive hydrogen bonding, a problem of interest to computational organic chemists.

The CCSD(T)/aug-cc-pVTZ//MP2/aug-cc-pVTZ energies of clusters 1-5 (shown in Figure 1) were obtained by Yoo.² These clusters are notable not just for their size but also that they involve multiple water molecules involved in four hydrogen bonds. Truhlar has used these geometries to compute the energies using 73 different density functionals with the jun-cc-pVTZ basis set (see this post for a definition of the ‘jun’ basis sets). Binding energies (relative to 16 isolated water molecules) were computed along with the 10 relative energies amongst the 5 different clusters. Combining the results of both types of energies, Truhlar finds that the best overall performance relative to CCSD(T) is obtained with ωB97X-D, a hybrid GGA method with a dispersion correction. The next two best performing functionals are LC-ωPBE-D3 and M05-2x. The best non-hybrid performance is with revPBE-D3 and B97-D.

1 (0.0)	2 (0.25)
3 (0.42)	4 (0.51)
5 (0.54)

Figure 1. MP2/aug-cc-pVTZ optimized geometries and relative CCSD(T) energies (kcal mol^-1) of (water)₁₆ clusters 1-5. (Don’t forget to click on any of these molecules above to launch Jmol to interactively view the 3-D structure. This feature is true for all molecular structures displayed in all of my blog posts.)

While this study can help guide selection of a functional, two words of caution. First, Truhlar notes that the best performing methods for the five (H₂O)₁₆ clusters do not do a particularly great job in getting the binding and relative energies of water hexamers, suggesting that no single functional really stands out as best. Second, a better study would also involve geometry optimization using that particular functional. Since this was not done, one can garner little here about what method might be best for use in a typical study where a geometry optimization must also be carried out.

References

(1) Leverentz, H. R.; Qi, H. W.; Truhlar, D. G. "Assessing the Accuracy of Density
Functional and Semiempirical Wave Function Methods for Water Nanoparticles: Comparing Binding and Relative Energies of (H₂O)₁₆ and (H₂O)₁₇ to CCSD(T) Results," J. Chem. Theor. Comput. 2013, ASAP, DOI: 10.1021/ct300848z.

(2) Yoo, S.; Aprà, E.; Zeng, X. C.; Xantheas, S. S. "High-Level Ab Initio Electronic Structure Calculations of Water Clusters (H₂O)₁₆ and (H₂O)₁₇: A New Global Minimum for (H₂O)₁₆," J. Phys. Chem. Lett. 2010, 1, 3122-3127, DOI: 10.1021/jz101245s.

Can a hydrogen bonding network affect acidity? Kass has examined the polyol 1 whose conjugate base 1cb can potentially be stabilized by a large hydrogen bonding network.¹ Kass had previously found a significant acidy enhancement in comparing t-butanol (ΔG(deprotonation) = 369.2 kcal mol^-1) with that of 2 (ΔG(deprotonation) = 334.4 kcal mol^-1).²

Table 1 lists the computed and experimental free energies of deprotonation of 1. The experimental values are computed at M06-2x/maug-cc-pVT(+d)Z. The structure of 1cb is drawn in Figure 1.

Table 1. Computed and experimental free energies (kcal mol^-1 of deprotonation of some alcohols.

The difference in the acidity of t-butanol and 2, some 30 kcal mol^-1, reflects the stability afforded by three intramolecular hydrogen bonds to the oxyanion. In going from 2cb to 1cb, each of the hydroxyl groups that donate to the oxyanion act as the acceptor of a hydrogen bond from the more removed hydroxyl groups. There is in effect a first and second layer of hydrogen bond network in 1cb. These secondary hydrogen bonds lead to further stabilization of the anion, as reflected in the diminished DPE of 1 over 2: 320.2 vs. 335.0 kcal mol^-1. Note that this secondary layer does not stabilize the anion to the same degree as the primary layer, but nonetheless its effect is large and quite striking.

1cb

Figure 1. M06-2x/maug-cc-pVT(+d)Z optimized structure of 1cb.

Even in solution these more remote hydrogen bonds can stabilize the anion. So, using the CPCM approach and modeling DMSO, 2 is predicted have a pK_a that is 15 units below that of t-butanol, and 1 is predicted to be 3 pK_a units more acidic than 2. Experiments verify this prediction with the pK_as of 16.1 for 2 and 11.4 for 1.

References

(1) Shokri, A.; Abedin, A.; Fattahi, A.; Kass, S. R. "Effect of Hydrogen Bonds on pKa Values: Importance of Networking," J. Am. Chem. Soc. 2012, 134, 10646-10650, DOI: 10.1021/ja3037349

(2) Tian, Z.; Fattahi, A.; Lis, L.; Kass, S. R. "Single-Centered Hydrogen-Bonded Enhanced Acidity (SHEA) Acids: A New Class of Brønsted Acids," J. Am. Chem. Soc. 2009, 131, 16984-16988, DOI: 10.1021/ja9075106

InChIs

1: InChI=1S/C13H28O7/c14-4-1-10(17)7-13(20,8-11(18)2-5-15)9-12(19)3-6-16/h10-12,14-20H,1-9H2
InChIKey=HGTVPOTWAYDRSM-UHFFFAOYSA-N

1cb: InChI=1S/C13H27O7/c14-4-1-10(17)7-13(20,8-11(18)2-5-15)9-12(19)3-6-16/h10-12,14-19H,1-9H2/q-1
InChIKey=UQPPTNIHRICITD-UHFFFAOYSA-N

2: InChI=1S/C7H16O4/c8-4-1-7(11,2-5-9)3-6-10/h8-11H,1-6H2
InChIKey=FAQWYKIIWYVDPQ-UHFFFAOYSA-N

2cb: InChI=1S/C7H15O4/c8-4-1-7(11,2-5-9)3-6-10/h8-10H,1-6H2/q-1
InChIKey=WSCPTRIAWKZJFZ-UHFFFAOYSA-N