I seem to be recently flooded with papers dealing with tunneling in organic systems. Well, here’s one more! Kozuch, Borden, Schreiner and co-workers seek out systems whereby isotopic substitution might lead to reaction selectivity.¹ Their base system is cyclopropylmethylcarbene 1, which can undergo three different reactions: (a) the ring can expand to give 1-methylcyclobut-1-ene 2, (b) a hydrogen can shift from the terminal methyl group to give vinylcyclopropane 3, or (c) the methane hydrogen can shift to produce ethylidenecyclopropane 4. This last option can be neglected since its barrier (20.5 kcal mol^-1) is so much higher than for the other two, 7.5 kcal mol^-1 for the ring expansion and 12.1 kcal mol^-1 for the [1,2]H-shift converting 1 → 3.

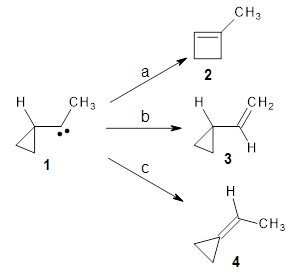
At high temperature, the ring expansion to 2 will dominate, but at low temperature the hydrogen shift to 3 might dominate by tunneling through the barrier due to the low mass and short distances involved. The reaction rates were computed using B3LYP/6-31G(d,p) and small-curvature tunneling. At low temperature, the rate for the hydrogen shift is 10 orders of magnitude faster than the ring expansion. Thinking that deuterium substitution of the terminal methyl group might slow down the rate of the [1,2]-shift, they computed the rates for the reactions of 1-d3, and in fact the rate of this shift does reduce by 10⁴ but it is still much faster than the rate for ring expansion. What is needed is a system where the rate for ring expansion is slower than the rate for hydrogen migration but faster than the rate of deuterium migration.

They examine a number of different substituents that may help to lower the barrier for the ring expansion. The methoxy derivative 5 turns out to suit the bill perfectly. The methoxy group reduces the barrier for ring expansion from 7.5 kcal mol^-1 with 1 to 2.5 kcal mol^-1 with 5. With hydrogenated 5, the [1,2]H-shift is 10³ times faster than ring expansion, but with deuterated 5, ring expansion is twice as fast as the deuterium migration.

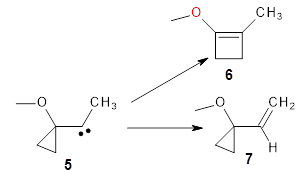
The authors call this isotope controlled selectivity (ICS), and this is the first example of this type of control.

References

1. Nandi, A.; Gerbig, D.; Schreiner, P. R.; Borden, W. T.; Kozuch, S., Isotope-Controlled Selectivity by Quantum Tunneling: Hydrogen Migration versus Ring Expansion in Cyclopropylmethylcarbenes. J. Am. Chem. Soc. 2017, 139, 9097-9099, DOI: 10.1021/jacs.7b04593.

InChIs

1: InChI=1S/C5H8/c1-2-5-3-4-5/h5H,3-4H2,1H3
InChIKey=KJIJNBZLGHBOTI-UHFFFAOYSA-N

2: InChIInChIKey=AVPHQXWAMGTQPF-UHFFFAOYSA-N

3: InChI=1S/C5H8/c1-2-5-3-4-5/h2,5H,1,3-4H2
InChIKey=YIWFBNMYFYINAD-UHFFFAOYSA-N

4: InChI=1S/C5H8/c1-2-5-3-4-5/h2H,3-4H2,1H3
InChIKey=ZIFNDRXSSPCNID-UHFFFAOYSA-N

5: InChI=1S/C6H10O/c1-3-6(7-2)4-5-6/h4-5H2,1-2H3
InChIKey=YMBSTCICUAORNN-UHFFFAOYSA-N

6: InChIInChIKey=QBLNAZHAVPMLHB-UHFFFAOYSA-N

7: InChIInChIKey=FHYLDABSPVPDTJ-UHFFFAOYSA-N

Last year I wrote a post on the possibility of a stable hypercoordinated carbon in the C(CH₃)₅⁺ molecule as proposed by Schleyer and Schaefer.¹ Kozuch has re-examined this molecule with an eye towards examining the lifetime of this proposed “fleeting” molecule.²

The computed barriers for either (1) loss of a methane molecule leaving behind the (CH₃)₂C⁺CH₂CH₃ cation or (2) loss of an ethane molecule leaving behind the t-butyl cation are small: 1.65 and 1.37 kcal mol^-1, respectively. Kozuch employed canonical variational theory with and without small curvature tunneling (SCT). Without the tunneling correction, the pentamethylmethyl cation is predicted to have a long (millennia) lifetime at very low temperatures (<20 K). However, when tunneling is included, the half-life is reduced to 6 and 40 μs for degradation along the two pathways. Clearly, this is not a fleeting molecule – its lifetime is really too short to consider it as anything.

Interestingly, perdeuterating the molecule ((CD₃)₅C⁺) substantially increases the half-life to 4 ms, a thousand-fold increase. Tritium substitution would further increase the half-life to 0.2 s – a long enough time to really identify it and perhaps justify the name “molecule”. What is perhaps the most interesting aspect here is that H/D substitution has such a large effect on the tunneling rate even though no C-H bond is broken in the TS! This results from a mass effect (a CH₃ vs. a CD₃ group is migrating) along with a zero-point vibrational energy effect.

References

(1) McKee, W. C.; Agarwal, J.; Schaefer, H. F.; Schleyer, P. v. R. "Covalent Hypercoordination: Can Carbon Bind Five Methyl Ligands?," Angew. Chem. Int. Ed. 2014, 53, 7875-7878, DOI: 10.1002/anie.201403314.

(2) Kozuch, S. "On the tunneling instability of a hypercoordinated carbocation," Phys. Chem. Chem. Phys. 2015, 17, 16688-16691, DOI: 10.1039/C5CP02080H.

InChIs

C(CH₃)₅⁺: InChI=1S/C6H15/c1-6(2,3,4)5/h1-5H3/q+1
InChIKey=GGCBGJZCTGZYFV-UHFFFAOYSA-N

Once again the Singleton group reports experiments and computations that require serious reconsideration of our notions of reaction mechanisms.¹ In this paper they examine the reaction of dichloroketene with labeled cis-2-butene. With ¹³C at the 2 position of 2-butene, two products are observed, 1 and 1’, in a ratio of 1’:1 = 0.993 ± 0.001. This is the opposite what one might have imagined based on the carbonyl carbon acting as an electrophile.

The first interesting item is that B3LYP/6-31+G** fails to predict the proper structure of the transition state. It predicts an asymmetric structure 2, shown in Figure 1, while MPW1k/6-31+G**, M06, and MP2 predict a C_s transition structure 3. The C_s TS is confirmed by a grid search of M06-2x geometries with CCSD(T)/6-311++G88/PCM(CH₂Cl₂) energies.

2

3

Figure 1. Optimized TSs 2 (B3LYP/6-31+G**) and 3 (MPW1K/6-31+G**).

The PES using proper computational methods is bifurcating past TS 3, falling downhill to product 1 or 1’. Lying on the C_s plane is a second transition state that interconverts 1 and 1’. On such a surface, conventional transition state theory would predict equal amounts of 1 and 1’, i.e. no isotope effect! So they must resort to a trajectory study – which would be impossibly long if not for the trick of making the labeled carbon super-heavy – like ²⁸C,⁴⁴C, ⁷⁶C and ¹⁴⁰C and then extrapolating back to just ordinary ¹³C. These trajectories indicate a ratio of 1’:1 of 0.990 in excellent agreement with the experimental value of 0.993.

Interestingly, most trajectories recross the TS, usually by reaching into the region near the second TS. However, the recrossing decreases with increasing isotopic mass, and this leads to the isotope effect. It turns out the vibrational mode 3 breaks the C_s symmetry; movement in one direction along mode 3 has no mass dependence but in the opposite direction, increased mass leads to decreased recrossing – or put in another way, in this direction, increased mass leads more often to product.

But one can understand this reaction from a statistical point of view as well. If one looks at the free energy surface, there is a variational TS near 3, but then there is a second set of variational transition states (one leading to 1 and one to 1’) which are associated with the formation of the second C-C bond. In a sense there is an intermediate past 3 that leads to two entropic barriers, one on a path to 1 and one on the path to 1’. RRKM using this model gives a ratio of 0.992 – again in agreement with experiment! It is as Singleton notes “perplexing”; how do you reconcile the statistical view with the dynamical (trajectory) view? Singleton has no full explanation.

Lastly, they point out that a similar situation occurs in the organocatalyzed Diels-Alder reaction of MacMillan shown below.² (This reaction is also discussed in a previous post.) Now Singleton finds that the “substituent effects, selectivity, solvent effects, isotope effects and activation parameters” are all dictated by a second variational TS far removed from the conventional electronic TS.

References

(1) Gonzalez-James, O. M.; Kwan, E. E.; Singleton, D. A., "Entropic Intermediates and Hidden Rate-Limiting Steps in Seemingly Concerted Cycloadditions. Observation, Prediction, and Origin of an Isotope Effect on Recrossing," J. Am. Chem. Soc. 2012, 134, 1914-1917, DOI: 10.1021/ja208779k

(2) Ahrendt, K. A.; Borths, C. J.; MacMillan, D. W. C., "New Strategies for Organic Catalysis: The First Highly Enantioselective Organocatalytic Diels-Alder Reaction," J. Am. Chem. Soc. 2000, 122, 4243-4244, DOI: 10.1021/ja000092s.

InChIs

2-butene: InChI=1/C4H8/c1-3-4-2/h3-4H,1-2H3/b4-3-
InChIKey=IAQRGUVFOMOMEM-ARJAWSKDBO

Dichloroketene: InChI=1/C2Cl2O/c3-2(4)1-5
InChIKey=TVWWMKZMZALOFP-UHFFFAOYAY

1 (no isotope): InChI=1/C6H8Cl2O/c1-3-4(2)6(7,8)5(3)9/h3-4H,1-2H3/t3-,4+/m0/s1
InChIKey=BAEYWHUXGUIZSP-IUYQGCFVBH

Suppose a compound could exist in one of two ways: (a) a symmetrical structure like the bromonium cation A or (b) equilibrating structures that on a time-average basis appear symmetrical, like B. How would one differentiate between these two possibilities?

Saunders developed a method whereby the species is isotopically labeled and then examined by NMR.^1-3 For case B, isotopic labeling will desymmetrize the two structures and so the chemical shifts of what were equivalent nuclei will become (often quite) different. But the isotopic labeling of A, while breaking the symmetry, does so to a much lesser extent, and the chemical shit difference of the (former) equivalent nuclei will be similar.

Singelton has employed this concept using both experiment and theory for two interesting cases.⁴ For the bromonium cation 1, Ohta⁵ discovered that the ¹³C NMR chemical shifts differed by 3.61 ppm with the deuterium labels. This led Ohta to conclude that the bomonium cation is really two equilibrating structures. It should be noted that the DFT optimized structure has C_2v symmetry (a single symmetric structure). Singleton applied a number of theoretical methods, the most interesting being an MD simulation of the cation. A large number of trajectories were computed and then the NMR shifts were computed at each point along each trajectory to provide a time-averaged difference in the chemical shifts of 4.8 ppm. Thus 2 can express a desymmetrization even though the unlabled structure is symmetric. This desymmetrization is due to coupling of vibrational modes involving the isotopes.

The second example is phthalate 2. Perrin observed a large ¹⁸O chemical shift difference upon isotopic labeling of one of the oxygen atoms, suggesting equilibrating structures.⁶ An MD study of such a system would take an estimated 1500 processor-years. Instead, by increasing the mass of the label to ²⁴O, the trajectories could be computed in a more reasonable time, and this would result in an isotope effect that is 4 times too large. The oxygen chemical shifts of more the 2.5 million trajectory points were computed for the two labeling cases, and each again showed a large chemical shift difference even though the underlying structure is symmetrical.

Thus, isotopic labeling can desymmetrize a symmetrical potential energy surface.

References

(1) Saunders, M.; Kates, M. R., "Isotopic perturbation of resonance. Carbon-13 nuclear magnetic resonance spectra of deuterated cyclohexenyl and cyclopentenyl cations," J. Am. Chem. Soc., 1977, 99, 8071-8072, DOI: 10.1021/ja00466a061

(2) Saunders, M.; Telkowski, L.; Kates, M. R., "Isotopic perturbation of degeneracy. Carbon-13 nuclear magnetic resonance spectra of dimethylcyclopentyl and dimethylnorbornyl cations," J. Am. Chem. Soc., 1977, 99, 8070-8071, DOI: 10.1021/ja00466a060

(3) Saunders, M.; Kates, M. R.; Wiberg, K. B.; Pratt, W., "Isotopic perturbation of resonance. Carbon-13 nuclear magnetic resonance of 2-deuterio-2-bicyclo[2.1.1]hexyl cation," J. Am. Chem. Soc., 1977, 99, 8072-8073, DOI: 10.1021/ja00466a062

(4) Bogle, X. S.; Singleton, D. A., "Isotope-Induced Desymmetrization Can Mimic
Isotopic Perturbation of Equilibria. On the Symmetry of Bromonium Ions and Hydrogen Bonds," J. Am. Chem. Soc., 2011, 133, 17172-17175, DOI: 10.1021/ja2084288

(5) Ohta, B. K.; Hough, R. E.; Schubert, J. W., "Evidence for β-Chlorocarbenium and β-Bromocarbenium Ions," Organic Letters, 2007, 9, 2317-2320, DOI: 10.1021/ol070673n

(6) Perrin, C. L., "Symmetry of hydrogen bonds in solution," Pure Appl. Chem., 2009, 81, 571-583, DOI: 10.1351/PAC-CON-08-08-14.

Kinetic isotope effects (KIE) are a valuable tool for probing mechanisms without changing the potential energy surface. Their interpretation can sometimes be difficult – for example is a perdeutero group larger or smaller than the perhydro analogue?

O’Leary, Rablen and Meyer have examined two related molecules and their KIEs relating to stereoinversion.¹ 1 exhibits a normal isotope effect (k_H/k_D = 1.06) while 2 has an inverse isotope effect (k_H/k_D = 0.880). They optimized the structures and transition states (see Figure 1) for racemization of both compounds at B3LYP and MP2, and computed isotope effects based on the Biegeleisen-Mayer equation (which is based on reduced partition functions). The KIEs obtained from the two computational methods is very similar.

1	1TS
2	2TS

Figure 1. MP2/6-31G(d,p) optimized geometries of 1 and 2 and the transition states for their racemization.

The experimental and computed KIEs are listed in Table 1. The agreement between experiment and computation is excellent – suggesting that computations should be routinely employed when analyzing isotope effects.

Table 1. Experimental and computed KIEs for racemization of 1 and 2.

The authors decompose the isotope effects into enthalpic and entropic components and note that the interplay between these two can be subtle – sometimes one might dominate and other times the second term will dominate, and the terms can be cooperative or non-cooperative.

References

(1) O’Leary, D. J.; Rablen, P. R.; Meyer, M. P., "On the Origin of Conformational Kinetic Isotope Effects," Angew. Chem. Int. Ed., 2011, 50, 2564-2567, DOI: 10.1002/anie.201007322

InChIs

1: InChI=1/C18H14O2/c19-15-7-11-3-1-4-12-8-16(20)10-14-6-2-5-13(9-15)18(14)17(11)12/h1-6H,7-10H2
InChIKey=DYZSIUYFWKNLHS-UHFFFAOYAB

d₈–1: InChI=1/C18H14O2/c19-15-7-11-3-1-4-12-8-16(20)10-14-6-2-5-13(9-15)18(14)17(11)12/h1-6H,7-10H2/i7D2,8D2,9D2,10D2
InChIKey=DYZSIUYFWKNLHS-UFBJYANTEO

2: InChI=1/C16H18/c1-11-5-3-7-13-9-10-14-8-4-6-12(2)16(14)15(11)13/h3-8,13,15H,9-10H2,1-2H3
InChIKey=OBRIKDRTDGHGIQ-UHFFFAOYAU