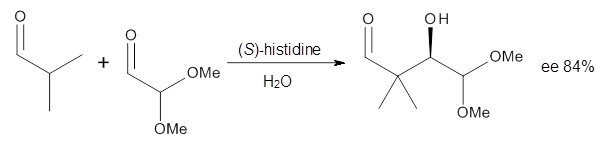
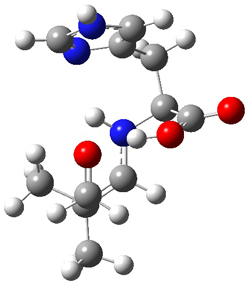
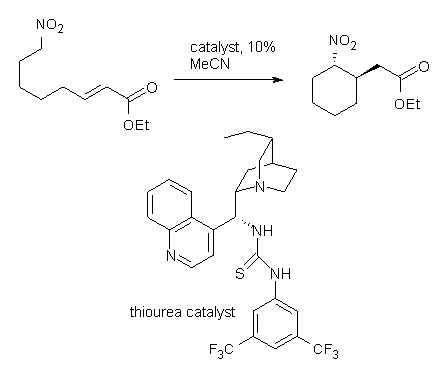
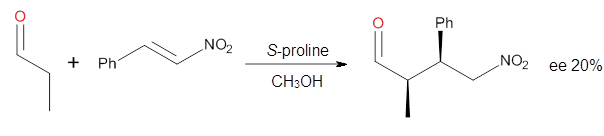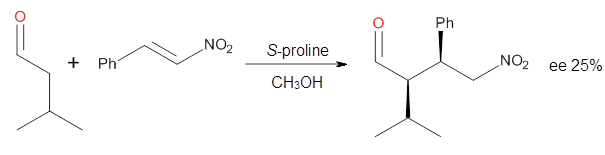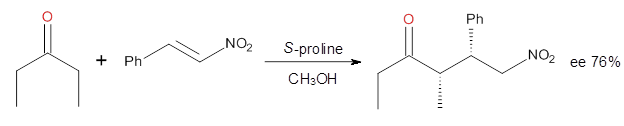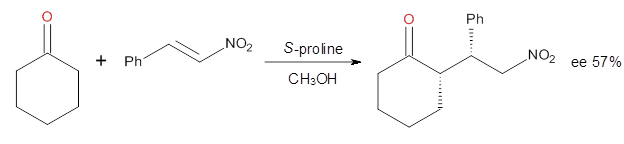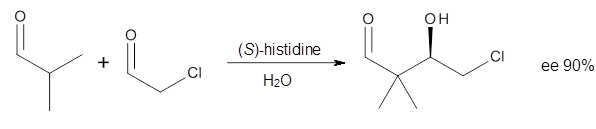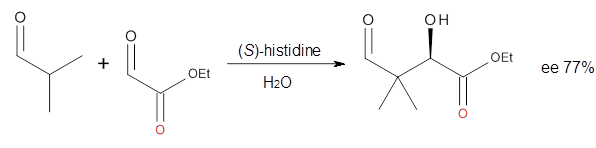Cinchona alkaloids cat catalyze reactions, such as shown in Reaction 1. Wynberg¹ proposed a model to explain the reaction, shown in Scheme 1, based on NMR. Grayson and Houk have now used DFT computations to show that the mechanism actually reverses the arrangements of the substrates.²

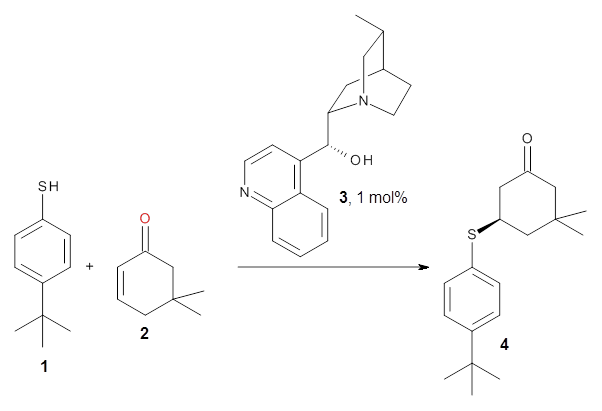
Reaction 1

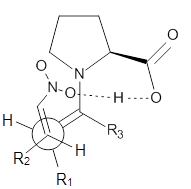
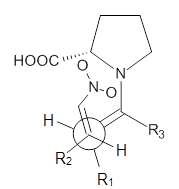
Scheme 1.

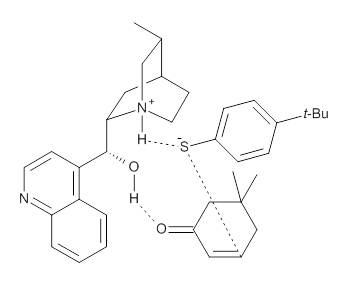
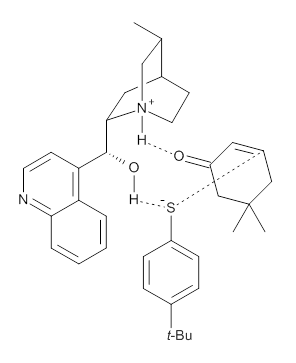
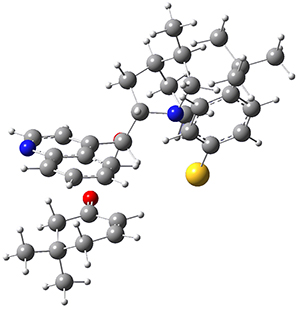
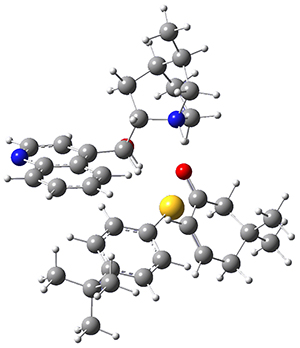
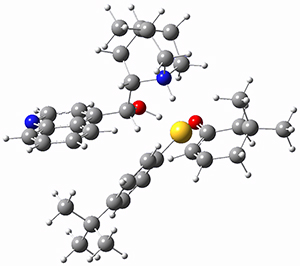
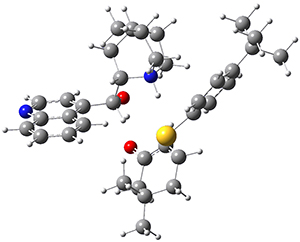
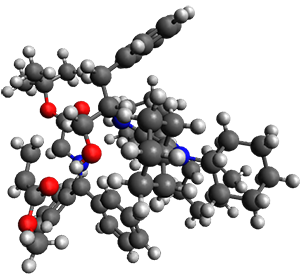
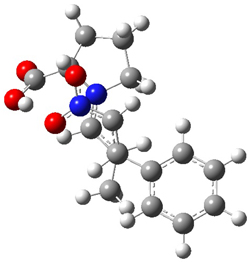
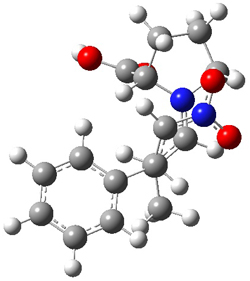
M06-2X/def2-TZVPP−IEFPCM(benzene)//M06-2X/6-31G(d)−IEFPCM(benzene) computations show that the precomplex of catalyst 3 with nucleophile 1 and Michael acceptor 2 is consistent with Wynberg’s model. The alternate precomplex is 5.6 kcal mol^-1 higher in energy. These precomplexes are shown in Figure 1.

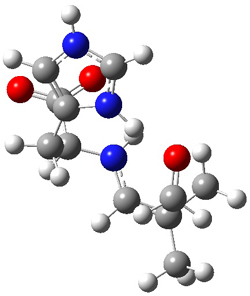
Wynberg precomplex

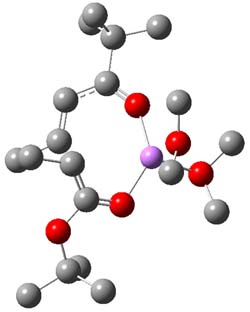
Grayson/Houk precomplex

Figure 1. Precomplexes structures

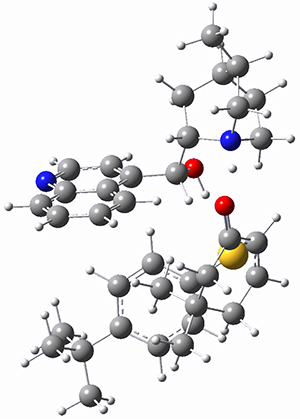
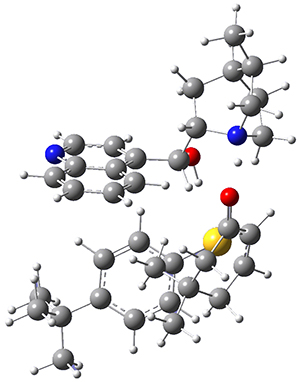
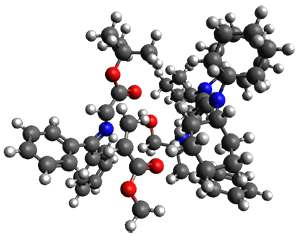
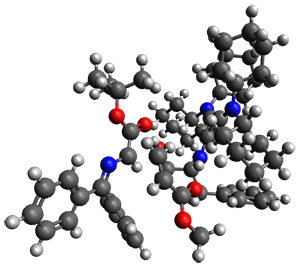
However, the lowest energy transition state takes the Grayson/Houk pathway and leads to the major isomer observed in the reaction. The Grayson/Houk TS that leads to the minor product has a barrier that is 3 kcal mol^-1 higher in energy. The lowest energy TS following the Wynberg path leads to the minor product, and is 2.2 kcal mol^-1 higher than the Grayson/Houk path. These transition states are shown in Figure 2. The upshot is that complex formation is not necessarily indicative of the transition state structure.

Wynberg TS (major) Rel ΔG = 5.3	Wynberg TS (minor) Rel ΔG = 2.2
Grayson/Houk TS (major) Rel ΔG = 0.0	Grayson/Houk TS (minor) Rel ΔG = 3.0

Figure 2. TS structures and relative free energies (kcal mol^-1).

References

(1) Hiemstra, H.; Wynberg, H. "Addition of aromatic thiols to conjugated cycloalkenones, catalyzed by chiral .beta.-hydroxy amines. A mechanistic study of homogeneous catalytic asymmetric synthesis," J. Am. Chem. Soc. 1981, 103, 417-430, DOI: 10.1021/ja00392a029.

(2) Grayson, M. N.; Houk, K. N. "Cinchona Alkaloid-Catalyzed Asymmetric Conjugate Additions: The Bifunctional Brønsted Acid–Hydrogen Bonding Model," J. Am. Chem. Soc. 2016, 138, 1170-1173, DOI: 10.1021/jacs.5b13275.

InChIs

1: InChI=1S/C10H14S/c1-10(2,3)8-4-6-9(11)7-5-8/h4-7,11H,1-3H3
InChIKey=GNXBFFHXJDZGEK-UHFFFAOYSA-N

2: InChI=1S/C8H12O/c1-8(2)5-3-4-7(9)6-8/h3-4H,5-6H2,1-2H3
InChIKey=CDDGRARTNILYAB-UHFFFAOYSA-N

3: InChI=1S/C18H22N2O/c1-12-11-20-9-7-13(12)10-17(20)18(21)15-6-8-19-16-5-3-2-4-14(15)16/h2-6,8,12-13,17-18,21H,7,9-11H2,1H3/t12?,13?,17?,18-/m1/s1
InChIKey=ZOZLJWFJLBUKKL-NKHWWFDVSA-N

4: InChI=1S/C18H26OS/c1-17(2,3)13-6-8-15(9-7-13)20-16-10-14(19)11-18(4,5)12-16/h6-9,16H,10-12H2,1-5H3/t16-/m0/s1
InChIKey=XUTYYZOSKLYWLW-INIZCTEOSA-N

Computational techniques are gaining some traction in helping to understand enantioselective organocatalysis. I talk about a few examples in Chapter 6.3 of my book. Lambert and Vetticatt have now used computations to help understand the role of the catalyst 4 in the Michael addition shown in Scheme 1.¹ This reaction proceeds with 99% yield and an ee of 98%.

Scheme 1.

¹³C kinetic isotope effect studies suggest that the rate determining step is the C-C bond formation (the Michael addition step) which follows the deprotonation of the imine 1 by the catalyst 4.

They performed ONIOM computations to search for transition states of this rate limiting step for the reaction in Scheme 1, using the full molecules. From this ONIOM search, the energies for all transition structures with 5 kcal mol^-1 of the lowest energy structure were then obtained at B3LYP/6-31G*. The three lowest energy TS are shown in Figure 1. The two lowest energy structures lead to the major enantiomer, while the third lowest energy structure leads to the minor enantiomer. These energies lead to a prediction of an ee of 92%, in reasonable agreement with the experiment. The computed kinetic isotope effects are in nice agreement with experiment, supporting this step as the overall rate limiting step.

TSs leading to the S isomer
TS1 (0.0)	TS2 (0.9)
TS leading to the R isomer
TS3 (1.7)

Table 1. ONIOM optimized geometries of the three lowest energy TSs. Relative energy (kcal mol^-1) in parenthesis.

Analysis of what factors are important in determining the ee is complicated and ultimately the authors are unable to provide a simple explanation. They properly note that

The observation that the major enantiomer (S) is formed from two very geometrically distinct transition structures … suggests that the prediction of enantioselectivity for other reactions … will require a full consideration of all possible transition state assemblies. (emphasis mine)

I agree with this sentiment, pessimistic as it may be. Answering this type of question is likely to remain very challenging for years to come.

References

1) Bandar, J. S.; Sauer, G. S.; Wulff, W. D.; Lambert, T. H.; Vetticatt, M. J. "Transition State Analysis of Enantioselective Brønsted Base Catalysis Chiral Cyclopropenimines," J. Am. Chem. Soc. 2014, 136, 10700-10707, DOI: 10.1021/ja504532d.

InChIs

1: InChI=1S/C20H23NO/c1-20(2,3)14-18(22)15-21-19(16-10-6-4-7-11-16)17-12-8-5-9-13-17/h4-13H,14-15H2,1-3H3
InChIKey=UZCWUGCTNCNJHI-UHFFFAOYSA-N

2: InChI=1S/C4H6O2/c1-3-4(5)6-2/h3H,1H2,2H3
InChIKey=BAPJBEWLBFYGME-UHFFFAOYSA-N

3: InChI=1S/C24H29NO3/c1-24(2,3)17-21(26)20(15-16-22(27)28-4)25-23(18-11-7-5-8-12-18)19-13-9-6-10-14-19/h5-14,20H,15-17H2,1-4H3/t20-/m0/s1
InChIKey=KTASCPHNNZODSX-FQEVSTJZSA-N

4: InChI=1S/C37H57N3/c1-2-30(28-29-18-8-3-9-19-29)38-35-36(39(31-20-10-4-11-21-31)32-22-12-5-13-23-32)37(35)40(33-24-14-6-15-25-33)34-26-16-7-17-27-34/h3,8-9,18-19,30-34H,2,4-7,10-17,20-28H2,1H3/t30-/m1/s1
InChIKey=GEHSIGXXLTVFFG-SSEXGKCCSA-N

Here are a couple of articles describing computational approaches to catalytic enantioselective reactions using variations upon the classic proline-catalyzed aldol reaction of List and Barbas¹ that started the whole parade. I have discussed the major computational papers on that system in my book (Chapter 5.3).

Yang and Wong² investigated the proline-catalyzed nitro-Michael reaction, looking at four examples, two with aldehydes and two with ketones (Reactions 1-4).

These four reactions were examined atMP2/311+G**//M06-2x/6-31G**, and PCM was also applied. The key element of this study is that they examined two different types of transition states: (a) based on the Houk-List model involving a hydrogen bond and (b) an electrostatic based model with no hydrogen bond. These are sketched in Scheme 1. For each of the reactions 1-4 there are 8 located transition states differing in the orientation of the attack on to the syn or anti enamine.

Scheme 1. TS models

The two lowest energy TS are shown in Figure 1. TS1-β1-RS is the lowest TS and it leads to the major enantiomer. The second lowest TS, TS1-β3-SR, lies 2.9 kJ mol^-1 above the other TS, and it leads to the minor enantiomer. This lowest TS is of the Houk-List type (Model A) while the other TS is of the Model B type. The enthalpies of activation suggest an ee of 54%, in reasonable
agreement with experiment.

TS1-β1-RS

TS1-β1-RS

Figure 1. M06-2x/6-31G** optimized geometries of TS1-β1-RS and TS1-β1-RS.

The computations of the other three reactions are equally good in terms of agreement with experiment, and importantly the computations indicate the reversal of stereoselection between the aldehydes and the ketones. These computations clearly implicate both the Houk-List and the non-hydrogen bonding TSs in the catalyzed Michael additions.

Houk in collaboration with Scheffler and Mahrwald investigate the use of histidine as a catalyst for the asymmetricaldol reaction.³ Examples of the histidine-catalyzed aldol are shown in Reactions 5-7.

	Reaction 5
	Reaction 6
	Reaction 7

The interesting twist here is whether the imidazole can also be involved in hydrogen bonding to the acceptor carbonyl group, serving the purpose of the carboxylic acid group in the Houk-List TS when proline is the catalyst (Model A). The transition states for these and a few other reactions were computed at M06-2x/6-31+G(d,p) including with the SMD continuum solvent model for water. The two lowest energy TSs for the reaction of isobutyraldehde and formaldehyde are shown in Figure 2; TS1 has the carboxylic acid group as the hydrogen donor while the imidazole is the donor in TS2. Of note is that these two TS are isoenergetic, indicating that both modes of stabilization are at play with histidine as the catalyst.

TS1

TS2

Figure 2. M06-2x/6-31+G(d,p) geometries of the two lowest energy TSs for the reaction of isobutyraldehde and formaldehyde catalyzed by histidine.

The possible TSs for Reactions 5-7 were also located. For example, with Reaction 5, the lowest energy TS involves the imidazole as the hydrogen donor and it leads to the major product. The lowest energy TS that leads to the minor product involves the carboxylic acid as the donor. The computed ee’s for Reactions 5-7 are in very good, if not excellent, agreement with the experimental values. The study should spur further activity in which one might tune the stereoselectivity by using catalysts with multiple binding opportunities.

References

(1) List, B.; Lerner, R. A.; Barbas, C. F., III; "Proline-Catalyzed Direct Asymmetric Aldol Reactions," J. Am. Chem. Soc., 2000, 122, 2395-2396, DOI: 10.1021/ja994280y.

(2) Yang, H.; Wong, M. W. "(S)-Proline-catalyzed nitro-Michael reactions: towards a better understanding of the catalytic mechanism and enantioselectivity," Org. Biomol. Chem.,
2012, 10, 3229-3235, DOI: 10.1039/C2OB06993H

(3) Lam, Y.-h.; Houk, K. N.; Scheffler, U.; Mahrwald, R. "Stereoselectivities of Histidine-Catalyzed Asymmetric Aldol Additions and Contrasts with Proline Catalysis: A Quantum Mechanical Analysis," J. Am. Chem. Soc. 2012, 134, 6286-6295, DOI: 10.1021/ja2118392

Heathcock’s model for predicting the stereo-outcome of Michael additions¹ involves a metal bridging across the two carbonyl oxygens. For Reaction 1, the model predicts that 1,2-syn product over the 1,2-anti product based on more favorable steric arrangements in TSA relative to TSB. Note that other rotatamers of these TS models are possible, but are presumed to be less favorable due to the inability of the metal cation to bridge the carbonyls. In fact, the syn:trans ratio for Reaction 1 is 95:5.

Kwan and Evans have examined this (and related) reactions at the M05-2x/6-31G(d) level.² Dimethyl ether is used as the model for the solvent. The lowest energy transition state for Reaction 1 is TS1, shown in Figure 1 with suppressed drawing of the hydrogens (though the JMol active image will include the hydrogens). This structure is actually more like TSC, a rotamer that was thought to not have a bridging metal. TS1 does have the bridging metal, and this is accomplished by having dihedral values of 40° instead of the ideal 60°. So, computations support the general conclusion of the Heathcock approach, with a modification of the possible inclusion of some other rotamers, though the stereoprediction is not altered.

TS1

Figure 1. M05-2x/6-31G(d) optimized structure of the lowest energy transition state of Reaction 1. Hydrogens are removed in the image for clarity, but the Jmol active image (which you can see by clicking on the above image) will include the hydrogen atoms.

References

(1) Oare, D. A.; Heathcock, C. H. In Topics in Stereochemistry; Eliel, E. L., Wilen, S. H., Eds.; Wiley: New York, 1989; Vol. 19, p 227-408.

(2) Kwan, E. E.; Evans, D. A., "Intermolecular Michael Reactions: A Computational Investigation," Org. Lett. 2010, 12, 5124–5127, DOI: 10.1021/ol102017v

Coming on the heels of the very nice combined computational/experimental study of the enantioselective Strecker reaction by Jacobsen (see this post), there’s this JACS communication that really disappoints in its use of computational chemistry. Cobb uses yet another chiral thiourea to produce the enantioselective intramolecular Michael addition of nitronoates (Reaction1).¹ The reaction goes with excellent diastereoselectivity and eneatioselectivity, and can even be done with a substrate to produce three chiral centers. This is very nice synthetic chemistry.

The lack of reactivity of the Z ester suggested that the thiourea must associate with both the nitro group and the ester carbonyl. The authors provide a B3LYP/3-21G complex of thiourea with a simple nitroester (once again without providing coordinates in the supporting materials!) to demonstrate this sort of association. But this single structure, at this very low computational level, with these simplified reagents, and lacking solvent (see Rzepa’s comment) really makes one wonder just what value this computation provides. It also goes to demonstrate just how much effort Jacobsen went through to provide substantive computational support for his proposed mechanism of action.

References

(1) Nodes, W. J.; Nutt, D. R.; Chippindale, A. M.; Cobb, A. J. A., "Enantioselective Intramolecular Michael Addition of Nitronates onto Conjugated Esters: Access to Cyclic γ-Amino Acids with up to Three Stereocenters," J. Am. Chem. Soc. 2009, 131, 16016-16017, DOI: 10.1021/ja9070915