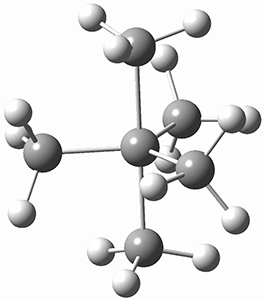
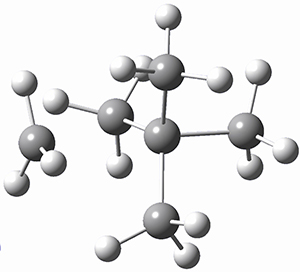
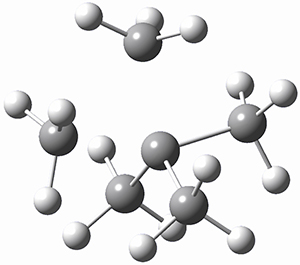
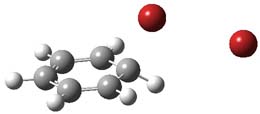
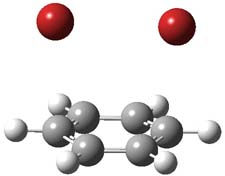
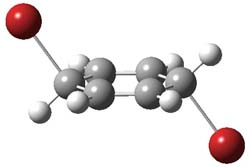
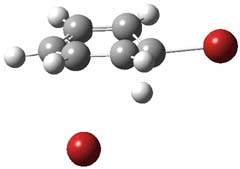
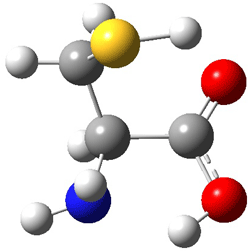
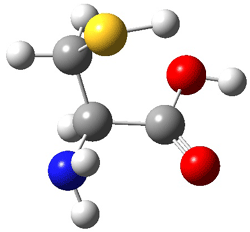
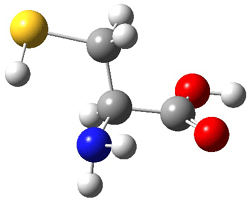
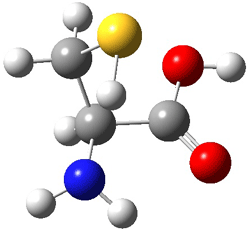
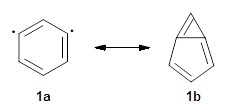
I want to update my discussion of m-benzyne, which I present in my book in Chapter 5.5.3. The interesting question concerning m-benzyne concerns its structure: is it a single ring structure 1a or a bicyclic structure 1b? Single configuration methods including closed-shell DFT methods predict the bicylic structure, but multi-configuration methods and unrestricted DFT predict it to be 1a. Experiments support the single ring structure 1a.

The key measurement distinguishing these two structure type is the C₁-C₃ distance. Table 1 updates Table 5.11 from my book with the computed value of this distance using some new methods. In particular, the state-specific multireference coupled cluster Mk-MRCCSD method¹ with the cc-pCVTZ basis set indicates a distance of 2.014 Å.² The density cumulant functional theory³ ODC-12⁴ with the cc-pCVTZ basis set also predicts the single ring structure with a distance of 2.101 Å.⁵

Table 1. C₁-C₃ distance (Å) with different computational methods using the cc-pCVTZ basis set

References

(1) Evangelista, F. A.; Allen, W. D.; Schaefer III, H. F. "Coupling term derivation and general implementation of state-specific multireference coupled cluster theories," J. Chem. Phys 2007, 127, 024102-024117, DOI: 10.1063/1.2743014.

(2) Jagau, T.-C.; Prochnow, E.; Evangelista, F. A.; Gauss, J. "Analytic gradients for Mukherjee’s multireference coupled-cluster method using two-configurational self-consistent-field orbitals," J. Chem. Phys. 2010, 132, 144110, DOI: 10.1063/1.3370847.

(3) Kutzelnigg, W. "Density-cumulant functional theory," J. Chem. Phys. 2006, 125, 171101, DOI: 10.1063/1.2387955.

(4) Sokolov, A. Y.; Schaefer, H. F. "Orbital-optimized density cumulant functional theory," J. Chem. Phys. 2013, 139, 204110, DOI: 10.1063/1.4833138.

(5) Mullinax, J. W.; Sokolov, A. Y.; Schaefer, H. F. "Can Density Cumulant Functional Theory Describe Static Correlation Effects?," J. Chem. Theor. Comput. 2015, 11, 2487-2495, DOI: 10.1021/acs.jctc.5b00346.

InChIs

1a: InChI=1S/C6H4/c1-2-4-6-5-3-1/h1-3,6H

Trying to get carbon to bond in unnatural ways seems to be a passion for many organic chemists! Schleyer has been interested in unusual carbon structures for decades and he and Schaefer now report a molecule with a pentacoordinate carbon bound to five other carbon atoms. Their proposed target is pentamethylmethane cation C(CH₃)₅⁺ 1.¹ The optimized geometry of 1, which has C_3h symmetry, at MP2/cc-pVTZ is shown in Figure 1. The bonds from the central carbon to the equatorial carbon are a rather long 1.612 Å, but the bonds to the axial carbon are even longer, namely 1.736 Å. Bader analysis shows five bond critical points, each connecting the central carbon to one of the methyl carbons. Wiberg bond index and MO analysis suggests that the central carbon is tetravalent, with a 2-electron-3-center bond involving the central and axial carbons.

1
TS1	TS2

Figure 1. MP2/cc-pVTZ optimized geometries of 1 and dissociation transition states.

So while 1 is a local energy minimum, it sits in a very shallow well. One computed dissociation path, which passes through TS1 (Figure 1) on its way to 2-methyl-butyl cation and methane has a barrier of only 1.65 kcal mol^-1 (CCSD(T)/CBS + ZPE). A second dissociation pathway goes through TS2 to t-butyl cation and ethane with a barrier of only 1.34 kcal mol^-1. Worse still is that the free energy estimates suggest “spontaneous dissociation … through both pathways”.

Undoubtedly, this will not be the last word on trying to torture a poor carbon atom.

References

(1) McKee, W. C.; Agarwal, J.; Schaefer, H. F.; Schleyer, P. v. R. "Covalent Hypercoordination: Can Carbon Bind Five Methyl Ligands?," Angew. Chem. Int. Ed. 2014, 53, 7875-7878, DOI: 10.1002/anie.201403314.

InChIs

1: InChI=1S/C6H15/c1-6(2,3,4)5/h1-5H3/q+1
InChIKey=GGCBGJZCTGZYFV-UHFFFAOYSA-N

“How small can a catenane be?” This question is asked by Schaefer, Allinger and colleagues and answered (well, almost answered) using computations.¹ Catenanes are linked rings. The catenanes examined here are two linked saturated hydrocarbon rings, each of the same size. The rings examined have 11 to 18 carbon atoms. The geometries were optimized with D₂ symmetry, where either the closest approach between the two rings are two carbon atoms or the midpoint of two C-C bonds. The former turn out to be lower in energy. Geometries were optimized with MP2, B3LYP, BP86 or M06-2X with the DZP++ basis set. There is little geometric dependence on computational method. The optimized geometry of the catenane with 14 carbons is shown in Figure 1.

Figure 1. Optimized geometry of the 14-carbon catenane. (Be sure to click on this structure to view the molecule in 3-D; you will have to allow Jmol to download and run!)

To cut to the chase, as the rings get smaller they observe a lengthening of the C-C bonds at the intersection. With the 14-carbon catenane they observe a significant increase in the bond length near the intersection, suggesting a dramatic instability. This is also seen in the change in the energy per C as the rings get smaller; a large increase in energy per C is seen at the transition from 14 to 13 carbons. This all points toward the 14-carbon catenane as the smallest one that might be stable.

(I thank Prof. Schaefer and colleagues for providing me with the coordinates of the 14-carbon catenane.)

References

(1) Feng, X.; Gu, J.; Chen, Q.; Lii, J.-H.; Allinger, N. L.; Xie, Y.; Schaefer, H. F. "How Small Can a Catenane Be?," J. Chem. Theor. Comput. 2014, 10, 1511-1517, DOI: 10.1021/ct400926p

Two interesting questions are addressed in a focal-point computational study of t-butyl radical and the t-butyl anion from the Schaefer group.¹ First, is the radical planar? EPR and PES studies from the 1970s indicate a pyramidal structure, with an inversion barrier of only 0.64 kcal mol^-1. The CCSD(T)/cc-pCVTZ optimized structure of t-butyl radical shows it to be pyramidal with the out-of-plane angle formed by one methyl group and the other three carbons of 22.9°, much less than the 54.7° of a perfect tetrahedron. Focal point analysis give the inversion barrier 0.74 kcal mol^-1, in outstanding agreement with experiment.

Second, what is the electron affinity (EA) of the t-butyl radical? Schleyer raised the concern that the alkyl anions may be unbound, and suggested that the electron affinity of t-butyl radical was -9.6 kcal mol^-1; in other words, the anion is thermodynamically unstable. This focal-point study shows just how sensitive the EA is to computational method. The HF/CBS value of the EA is -39.59 kcal mol^-1 (unbound anion), but the MP2/CBS value is +41.57 kcal mol^-1 (bound anion!). The CCSD/aug-cc-pVQZ value is -8.92 while the CCSD(T)/aug-cc-pVQZ value is +4.79 kcal mol^-1. The estimated EA at CCSDT(Q)/CBS is -1.88 kcal mol^-1, and inclusion of correction terms (including ZPE and relativistic effect) gives a final estimate of the EA as -0.48 kcal mol^-1, or a very weakly unbound t-butyl anion. It is somewhat disconcerting that such high-level computations are truly needed for some relatively simple questions about small molecules.

References

(1) Sokolov, A. Y.; Mittal, S.; Simmonett, A. C.; Schaefer, H. F. "Characterization of the t-Butyl Radical and Its Elusive Anion," J. Chem. Theory Comput. 2012, 8, 4323-4329, DOI: 10.1021/ct300753d.

We have all learned about aromatic substitution as proceeding via the following mechanism

(Worse yet – many of us have taught this for years!) Well, Galabov, Zou, Schaefer and Schleyer pour a whole lot of cold water on this notion in their recent Angewandte article.¹ Modeling the reaction of benzene with Br₂ and using B3LYP/6-311+G(2d,2p) for both the gas phase and PCM simulating a CCl₄ solvent, attempts to locate this standard intermediate led instead to a concerted substitution transition state TS1 (see Figure 1).

TS1

Figure 1. PCM/B3LYP/6-311+G(2d,2p) optimized transitin state along the concerted pathway

However, this is not the lowest energy pathway for substitution. Rather and addition-elimination pathway is kinetically preferred. In the first step Br₂ adds in either a 1,2 or 1,4 fashion to form an intermediate. The lower energy path is the 1,4 addition, leading to P3. This intermediate then undergoes a syn,anti-isomerization to give P5. The last step is the elimination of HBr from P5 to give the product, bromobenzene. This mechanism is shown in Scheme 2 and the critical points are shown in Figure 3.

Scheme 1

TS3	P3
TS6	P5
TS9

Figure 2. PCM/B3LYP/6-311+G(2d,2p) optimized critical points along the addition-elimination pathway

The barrier for the concerted substitution process through TS1 is 41.8 kcal mol^-1 (in CCl₄) while the highest barrier for the addition-elimination process is through TS3 of 39.4 kcal mol^-1.

Now a bit of saving grace is that in polar solvents, acidic solvents and/or with Lewis acid catalysts, the intermediate of the standard textbook mechanism may be competitive.

Textbook authors – please be aware!

References

(1) Kong, J.; Galabov, B.; Koleva, G.; Zou, J.-J.; Schaefer, H. F.; Schleyer, P. v. R., "The Inherent Competition between Addition and Substitution Reactions of Br₂ with Benzene and Arenes," Angew. Chem. Int. Ed. 2011, 50, 6809-6813, DOI: 10.1002/anie.201101852

Small energy differences pose a serious challenge for computation. The focal point analysis of Allen and Schaefer is one approach towards solving this problem, with energies extrapolated to the complete basis set limit at the HF and MP2 levels, and then corrections added on for higher-order effects.

These authors have applied the method to the conformations of alanine (similar to their previous study on cysteine – see this post).¹ There are two low energy conformers 1 and 2. The CCSD(T)/cc-pVTZ structures are shown in Figure 1. The HF/CBS estimate places 2 below 1, but this is reveres at MP2. With the correction for CCSD and CCSD(T), and core electrons, the energy gap is only 0.45 kJ mol^-1, favoring 1. Zero-point vibrational energy favors 1 by 1.66 kJ mol^-1, for a prediction that 1 is 2.11 kJ mol^-1 lower in energy than 2. It is interesting that most of this energy difference arises from differences in their ZPVE.

1

2

Figure 1. CCSD(T)/cc-pVTZ optimized geometries of the two lowest energy conformations of alanine.

The article also discusses the structures of these to conformers, obtained through a combination of theoretical treatment and revisiting the limited experimental measurements.

References

(1) Jaeger, H. M.; Schaefer, H. F.; Demaison, J.; Csaszar, A. G.; Allen, W. D., "Lowest-Lying Conformers of Alanine: Pushing Theory to Ascertain Precise Energetics and Semiexperimental R_e Structures," J. Chem. Theory Comput., 2010, 6, 3066-3078, DOI: 10.1021/ct1000236

InChIs

Alanine: InChI=1/C3H7NO2/c1-2(4)3(5)6/h2H,4H2,1H3,(H,5,6)/t2-/m0/s1/f/h5H
InChIKey=QNAYBMKLOCPYGJ-SNQCPAJUDI

An emerging theme in this blog is Möbius systems, ones that can be aromatic or antiaromatic. Rzepa has led the way here, especially in examining annulenes with a twisted structure. Along with Schleyer and Schaefer, they have now explored a series of Möbius annulenes.¹ The particularly novel aspect of this new work is the examination of higher-order Möbius systems. In the commonly held notion of the Möbius strip, the strip contains a single half twist. Rzepa points out that the notion of twist must be considered as two parts, a part due to torsions and a part due to writhe.² We can think of the Möbius strip as formed by a ladder where the ends are connect such that the left bottom post connects with the top right post and the bottom right post connects with the top left post. Let’s now consider the circle created by joining the midpoints of each rug of the ladder. If this circle lies in a plane, then the torsion is π/N where N is the number of rungs in the ladder. But, the collection of midpoints does not have to lie in a plane, and if these points distort out of plane, that’s writhe and allows for less torsion in the strip.The sum of these two parts is called L_k and it will be an integral multiple of π. So the common Möbius strip has L_k = 1.

An example of a molecular analogue of the common Möbius strip is the annulene C₉H₉⁺ (1) – see figure 1. But Möbius strips can have more than one twist. Rzepa, Schleyer, and Schaefer have found examples with L_k = 2, 3, or 4. Examples are C₁₄H₁₄ (2) with one full twist (L_k = 2, two half twists), C₁₆H₁₆^2- (3) with three half twists, and C₂₀H₂₀²⁺ (4) with four half twists.

1	2
3	4

Figure 1. Structures of annulenes 1-4.

These annulenes with higher-order twisting, namely 2-4, are aromatic, as determined by a variety of measures. For example, all express negative NICS values, all have positive diagmagnetic exaltations, and all express positive isomerization stabilization energies (which are a measure of aromatic stabilization energy).

References

(1) Wannere, C. S.; Rzepa, H. S.; Rinderspacher, B. C.; Paul, A.; Allan, C. S. M.; Schaefer Iii, H. F.; Schleyer, P. v. R., "The Geometry and Electronic Topology of Higher-Order Charged M&oml;bius Annulenes" J. Phys. Chem. A 2009, ASAP, DOI: 10.1021/jp902176a

(2) Fowler, P. W.; Rzepa, H. S., "Aromaticity rules for cycles with arbitrary numbers of half-twists," Phys. Chem. Chem. Phys. 2006, 8, 1775-1777, DOI: 10.1039/b601655c.

Schaefer, Csaszar, and Allen have applied the focal point method towards predicting the energies and structures of cysteine.¹ This very high level method refines the structures that can be used to compare against those observed by Alonso² in his laser ablation molecular beam Fourier transform microwave spectroscopy experiment (see this post). They performed a broad conformation search, initially examining some 66,664 structures. These reduced to 71 unique conformations at MP2/cc-pvTZ. The lowest 11 energy structures were further optimized at MP2(FC)/aug-cc-pV(T+d)Z. The four lowest energy conformations are shown in Figure 1 along with their relative energies.

I (0.0)	II (4.79)
III (5.81)	IV (5.95)

Figure 1. MP2(FC)/aug-cc-pV(T+d)Z optimized geometries and focal point relative energies (kJ mol^-1) of the four lowest energy conformers of cysteine.¹

The three lowest energy structures found here match up with the lowest two structures found by Alonso and the energy differences are also quite comparable: 4.79 kJ and 5.81 mol^-1 with the focal point method 3.89 and 5.38 kJ mol^-1 with MP4/6-311++G(d,p)// MP2/6-311++G(d,p). So the identification of the cysteine conformers made by Alonso remains on firm ground.

References

(1) Wilke, J. J.; Lind, M. C.; Schaefer, H. F.; Csaszar, A. G.; Allen, W. D., "Conformers of Gaseous Cysteine," J. Chem. Theory Comput. 2009, DOI: 10.1021/ct900005c.

(2) Sanz, M. E.; Blanco, S.; López, J. C.; Alonso, J. L., "Rotational Probes of Six Conformers of Neutral Cysteine," Angew. Chem. Int. Ed. 2008, 4, 6216-6220, DOI: 10.1002/anie.200801337

InChIs

Cysteine:
InChI=1/C3H7NO2S/c4-2(1-7)3(5)6/h2,7H,1,4H2,(H,5,6)/t2-/m0/s1
InChIKey: XUJNEKJLAYXESH-REOHCLBHBU

Malonaldehyde 1 possesses a very short intramolecular hydrogen bond. Its potential energy surface has two local minima (the two mirror image hydrogen-bonded structures) separated by a C_2v transition state. Schaefer reports a high-level computational study for the search for even shorter hydrogen bonds that might even lead to a single well on the PES.¹

The hydrogen bond distance is characterized by the non-bonding separation between the two oxygen atoms. Table 1 shows the O^…O distance for a number of substituted malonaldehydes computed at B3LYP/DZP++. Electron withdrawing groups on C₂ reduce the O^..O distance (see trend in 1 → 4). Electron donating groups on C₁ and C₃ also reduce this distance (see 5 and 6). Bulky substituents on the terminal carbons also reduce the O^…O distance (see 7). Combining all of these substituent effects in 8 leads to the very short O^…O distance of 2.380 Å.

Table 1. Distance (Å) between the two oxygen atoms and the barrier for hydrogen transfer of substituted malonaldehydes .¹

^aFocal point energy. ^bFocal point energy and corrected for zero-point vibrational energy.

A shorter O^…O distance might imply a smaller barrier for hydrogen transfer between the two oxygens. The structures of 8 and the transition state for its hydrogen transfer are shown in Figure 1. The energies of a number of substituted malonaldehydes were computed using the focal point method, and the barriers for hydrogen transfer are listed in Table 1. There is a nice correlation between the O^…O distance and the barrier height. The barrier for 8 is quite small, suggesting that with some bulkier substituents, the barrier might vanish altogether, leaving only a symmetric structure. In fact, the barrier appears to vanish when zero-point vibrational energies are included.

8

8TS

Figure 1. B3LYP/DZP++ optimized geometries of 8 and the transition state for hydrogen transfer 8TS.¹

References

(1) Hargis, J. C.; Evangelista, F. A.; Ingels, J. B.; Schaefer, H. F., "Short Intramolecular Hydrogen Bonds: Derivatives of Malonaldehyde with Symmetrical Substituents," J. Am. Chem. Soc., 2008, 130, 17471-17478, DOI: 10.1021/ja8060672.

InChIs

1: InChI=1/C3H4O2/c4-2-1-3-5/h1-4H/b2-1-
InChIKey=GMSHJLUJOABYOM-UPHRSURJBI

2: InChI=1/C4H3NO2/c5-1-4(2-6)3-7/h2-3,6H/b4-2-
InChIKey=BHYIQMFSOGUTRT-RQOWECAXBC

3: InChI=1/C3H3NO4/c5-1-3(2-6)4(7)8/h1-2,5H/b3-1+
InChIKey=JBBHDCMVSJADCE-HNQUOIGGBS

4: InChI=1/C3H5BO2/c4-3(1-5)2-6/h1-2,5H,4H2/b3-1+
InChIKey=IQNKNZSFMBIPBI-HNQUOIGGBX

5: InChI=1/C3H6N2O2/c4-2(6)1-3(5)7/h1,6H,4H2,(H2,5,7)/b2-1-/f/h5H2
InChIKey=AOZIOAJNRYLOAH-KRHGAQEYDI

6: InChI=1/C5H8O4/c1-8-4(6)3-5(7)9-2/h3,6H,1-2H3/b4-3+
InChIKey=BYYYYPBUMVENKB-ONEGZZNKBI

7: InChI=1/C11H20O2/c1-10(2,3)8(12)7-9(13)11(4,5)6/h7,12H,1-6H3/b8-7-
InChIKey=SOZFXLUMSLXZFW-FPLPWBNLBX

8: InChI=1/C3H5N3O4/c4-2(7)1(3(5)8)6(9)10/h7H,4H2,(H2,5,8)/b2-1+/f/h5H2
InChIKey=IHYUFGCOUITNJP-CHFMFTGODK

Angewandte Chemie has published a rather unusual short article – an appeal by Roald Hoffmann, Paul Schleyer and Fritz Schaefer (the latter two were interviewed in my book!) to use “more realism, please!”¹

These noted computational chemists suggest that we all have been sloppy in the language we use in describing our computations. They first take on the term “stable”, and rightfully point out that this is a very contextual term – stable where? on my desktop? In a 1M aqueous solution? Inside a helium glove box? Inside a mass spectrometer? In an interstellar cloud? Stable for how long? Indefinitely? For a day? For a day in the humid weather of San Antonio? Or a day inside a cold refrigerator? Or how about inside a Ne matrix? Or for the time it takes to run a picosecond laser experiment?

The authors offer up the terms “viable” and “fleeting” as reasonable alternatives and proscribe a protocol for meeting the condition of “viable” – and I must note that this protocol is very demanding, likely beyond the computational abilities of many labs and certainly beyond what can be done for a reasonably large molecule.

They also take on the uncertainty of computed results, pointing out the likely largely overlooked irreproducibility of many DFT results, due to size difference of the computed grids, difference in implementation of the supposedly same functional, etc. They conclude with a discussion of how many significant figures one should employ.

None of this is earth-shattering, and most is really well-known yet often neglected or overlooked. In another interesting publication treat in this issue, four referee reports of the article are reproduced. The first, by Gernot Frenking,² argues exactly this point – that the lack of new information, and the sort of whimsical literary approach make the article unacceptable for publication. The other three referees disagree,^3-5 and note that though the article is not novel, the authors forcefully remind us that better behaviors should be put into practice.

The article is a nice reminder that careful studies should be carefully reported. (And both the authors of the article and the referees note that these same comments apply to our experimental colleagues, too.)

References

(1) Hoffmann, R.; Schleyer, P. v. R.; Schaefer III, H. F., “Predicting Molecules – More Realism, Please!,” Angew. Chem. Int. Ed., 2008, 47, 7164-7167, DOI: 10.1002/anie.200801206.

(2) Frenking, G., “No Important Suggestions,” Angew. Chem. Int. Ed. 2008, 47, 7168-7169, doi: 10.1002/anie.200802500.

(3) Koch, W., “Excellent, Valuable, and Entertaining,” Angew. Chem. Int. Ed., 2008, 47, 7170, DOI: 10.1002/anie.200802996.

(4) Reiher, M., “Important for the Definition of Terminology in Computational Chemistry,” Angew. Chem. Int. Ed., 2008, 48, 7171, DOI: 10.1002/anie.200802506.

(5) Bickelhaupt, F. M., “Attractive and Convincing,” Angew. Chem. Int. Ed., 2008, 47, 7172, DOI: 10.1002/anie.200802330.