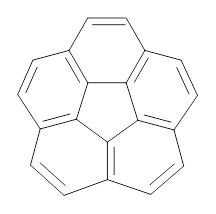
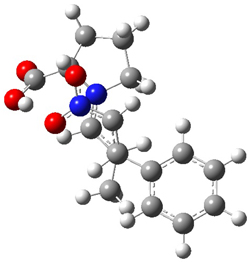
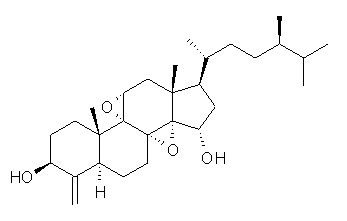
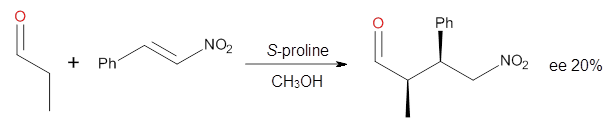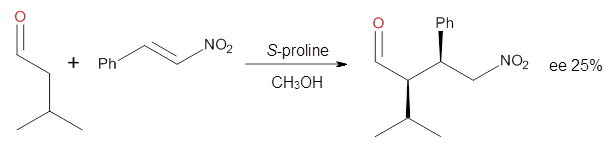How should one assess the aromatic stabilization energy of non-planar compounds like corannulene 1? The standard approach might be to employ the homodesmotic reaction, like Reaction 1. The energy of this reaction is however quite different whether one chooses s-cis or s-trans butadiene: 67.5 kcal mol^-1 with the former and 14.8 kcal mol^-1 with the latter. Exactly how one balances the total number of cis/trans relationships is problematic, but worse still is that Reaction 1 does not remove the effect of strain and non-planarity of 1.

1

2

Reaction 1
15 H₂C=CH-CH=CH₂ + 20 H₂C=C(CH₃)₂ → 1 + 10 H₂C=CH₂ + 20 H₂C=CH-CH₃

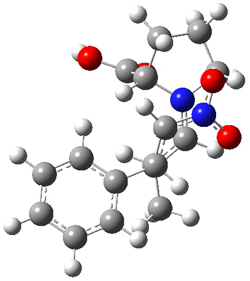
Dobrowolski, Ciesielski and Cyranski¹ propose a series of reactions that extend the isomerization stabilization energy concept of Schleyer. References are chosen that involve fixed alternate polyenes by appending methylene groups, creating radialene-like compounds. Reaction 2 and 3 are two such reactions that attempt to remove strain and non-planarity effects along with balancing the cis/trans relationships and potential H-H clashes between the pendant methylene groups. They report an additional 18 variations, because there is no unique method for portioning these effects.

Reaction 2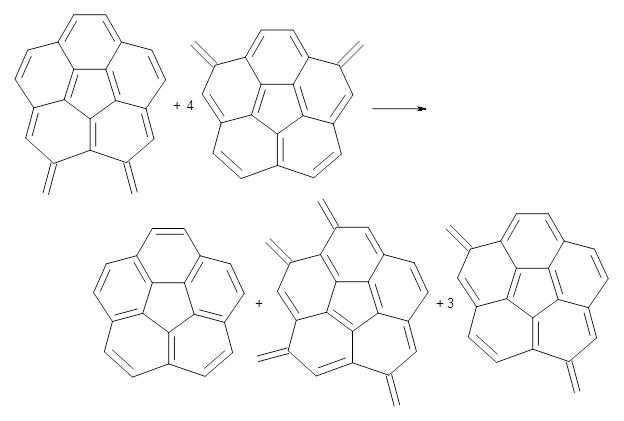

Reaction 3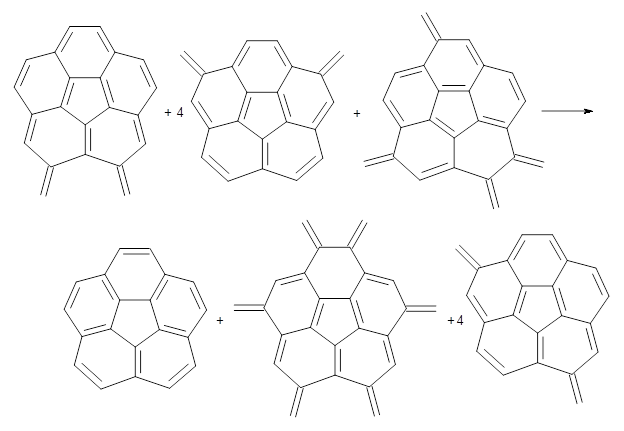

Using B3LYP/6-311G** energies with zero-point vibrational energy, the reaction energies are 46.7 and 46.3 kcal mol^-1 for Reactions 2 and 3, respectively. Using all of the variations, the mean value is 44.7 kcal mol^-1 with a standard deviation of only 1.2 kcal mol^-1. It is clear that corranulene has a rather substantial artomatic stabilization energy, reflecting its decided aromatic character.

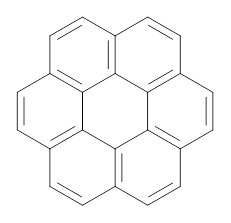
In a similar vein, they have also estimated the aromatic stabilization energy of coronene 2 as 58.4 kcal mol^-1, which, while clearly demonstrating the 2 is aromatic, it does not express any “superaromaticity”.

References

(1) Dobrowolski, M. A.; Ciesielski, A.; Cyranski, M. K. "On the aromatic stabilization of corannulene and coronene," Phys. Chem. Chem. Phys., 2011, 13, 20557-20563, DOI: 10.1039/C1CP21994D

InChIs

1: InChI=1S/C21H14/c1-3-13-6-7-15-10-11-16-9-8-14-5-4-12(2)17-18(13)20(15)21(16)19(14)17/h3-11H,1H2,2H3
InChIKey=ZJQHTVPYWDRMLD-UHFFFAOYSA-N

2: InChI=1S/C24H12/c1-2-14-5-6-16-9-11-18-12-10-17-8-7-15-4-3-13(1)19-20(14)22(16)24(18)23(17)21(15)19/h1-12H
InChIKey=VPUGDVKSAQVFFS-UHFFFAOYSA-N

Here are a couple of articles describing computational approaches to catalytic enantioselective reactions using variations upon the classic proline-catalyzed aldol reaction of List and Barbas¹ that started the whole parade. I have discussed the major computational papers on that system in my book (Chapter 5.3).

Yang and Wong² investigated the proline-catalyzed nitro-Michael reaction, looking at four examples, two with aldehydes and two with ketones (Reactions 1-4).

Reaction 1

Reaction 2

Reaction 3

Reaction 4

These four reactions were examined atMP2/311+G**//M06-2x/6-31G**, and PCM was also applied. The key element of this study is that they examined two different types of transition states: (a) based on the Houk-List model involving a hydrogen bond and (b) an electrostatic based model with no hydrogen bond. These are sketched in Scheme 1. For each of the reactions 1-4 there are 8 located transition states differing in the orientation of the attack on to the syn or anti enamine.

Scheme 1. TS models

Model A

Model B

The two lowest energy TS are shown in Figure 1. TS1-β1-RS is the lowest TS and it leads to the major enantiomer. The second lowest TS, TS1-β3-SR, lies 2.9 kJ mol^-1 above the other TS, and it leads to the minor enantiomer. This lowest TS is of the Houk-List type (Model A) while the other TS is of the Model B type. The enthalpies of activation suggest an ee of 54%, in reasonable
agreement with experiment.

TS1-β1-RS

TS1-β1-RS

Figure 1. M06-2x/6-31G** optimized geometries of TS1-β1-RS and TS1-β1-RS.

The computations of the other three reactions are equally good in terms of agreement with experiment, and importantly the computations indicate the reversal of stereoselection between the aldehydes and the ketones. These computations clearly implicate both the Houk-List and the non-hydrogen bonding TSs in the catalyzed Michael additions.

Houk in collaboration with Scheffler and Mahrwald investigate the use of histidine as a catalyst for the asymmetricaldol reaction.³ Examples of the histidine-catalyzed aldol are shown in Reactions 5-7.

	Reaction 5
	Reaction 6
	Reaction 7

The interesting twist here is whether the imidazole can also be involved in hydrogen bonding to the acceptor carbonyl group, serving the purpose of the carboxylic acid group in the Houk-List TS when proline is the catalyst (Model A). The transition states for these and a few other reactions were computed at M06-2x/6-31+G(d,p) including with the SMD continuum solvent model for water. The two lowest energy TSs for the reaction of isobutyraldehde and formaldehyde are shown in Figure 2; TS1 has the carboxylic acid group as the hydrogen donor while the imidazole is the donor in TS2. Of note is that these two TS are isoenergetic, indicating that both modes of stabilization are at play with histidine as the catalyst.

TS1

TS2

Figure 2. M06-2x/6-31+G(d,p) geometries of the two lowest energy TSs for the reaction of isobutyraldehde and formaldehyde catalyzed by histidine.

The possible TSs for Reactions 5-7 were also located. For example, with Reaction 5, the lowest energy TS involves the imidazole as the hydrogen donor and it leads to the major product. The lowest energy TS that leads to the minor product involves the carboxylic acid as the donor. The computed ee’s for Reactions 5-7 are in very good, if not excellent, agreement with the experimental values. The study should spur further activity in which one might tune the stereoselectivity by using catalysts with multiple binding opportunities.

References

(1) List, B.; Lerner, R. A.; Barbas, C. F., III; "Proline-Catalyzed Direct Asymmetric Aldol Reactions," J. Am. Chem. Soc., 2000, 122, 2395-2396, DOI: 10.1021/ja994280y.

(2) Yang, H.; Wong, M. W. "(S)-Proline-catalyzed nitro-Michael reactions: towards a better understanding of the catalytic mechanism and enantioselectivity," Org. Biomol. Chem.,
2012, 10, 3229-3235, DOI: 10.1039/C2OB06993H

(3) Lam, Y.-h.; Houk, K. N.; Scheffler, U.; Mahrwald, R. "Stereoselectivities of Histidine-Catalyzed Asymmetric Aldol Additions and Contrasts with Proline Catalysis: A Quantum Mechanical Analysis," J. Am. Chem. Soc. 2012, 134, 6286-6295, DOI: 10.1021/ja2118392

Here is an interesting twist on using computations in conjunction with experimental NMR to solve for molecular structure. I have blogged a number of times on comparing computed chemical shifts with experimental values to identify structure, and also on using the comparison of computed and experimental coupling constants to accomplish this purpose.

Butts and Bifulco were interested in the structure of conicasterol F 1 and opted to make two sets of comparison.¹ The first uses the traditional approach of comparing the computed and experimental ¹³C chemical shifts. The second comparison uses the distances between protons, coming from the optimized structure and the rotating-frame nuclear Overhauser effect (ROE).

Standard analysis of the NMR spectra of 1 allowed for the determination of all of the stereochemistry except for the epoxy ring at C₈ and C₁₄. The possible options are shown as 1a and 1b. The optimized geometries (MPW1PW91/6-31G) of these two diastereomers are shown in Figure 1.

1a	1b
1a	1b

Figure 1. Optimized geometries of 1a and 1b.

Comparison of 15 distances between protons determined by the ROE experiment and by computation led to a mean absolute error of 7.8% for 1a and 3.0% for 1b, suggesting that the latter is the correct structure. Similar comparison was then made between the experimental chemical shifts of 12 of the carbon atoms with the computed values of the two isomers. The mean absolute error in the chemical shifts of 1a is 3.7ppm, but only 0.8 ppm for 1b. Both methods give the same conclusion: conicasterol F has structure 1b.

References

(1) Chini, M. G.; Jones, C. R.; Zampella, A.; D’Auria, M. V.; Renga, B.; Fiorucci, S.; Butts, C. P.; Bifulco, G., "Quantitative NMR-Derived Interproton Distances Combined with Quantum Mechanical Calculations of ¹³C Chemical Shifts in the Stereochemical Determination of Conicasterol F, a Nuclear Receptor Ligand from Theonella swinhoei," J. Org. Chem., 2012, 77, 1489-1496, DOI: 10.1021/jo2023763.

InChIs

1b: InChI=1/C29H46O4/c1-16(2)17(3)8-9-18(4)21-14-23(31)28-26(21,7)15-24-29(32-24)25(6)12-11-22(30)19(5)20(25)10-13-27(28,29)33-28/h16-18,20-24,30-31H,5,8-15H2,1-4,6-7H3/t17-,18-,20+,21-,22+,23+,24-,25+,26-,27+,28+,29+/m1/s1
InChIKey=XTWHHLLDFQALAM-XAIGNWORBC