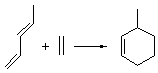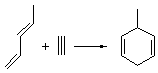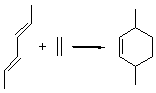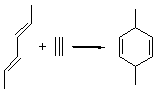The planar substituted cyclooctatetraene 1 has been prepared and characterized.¹ The B3LYP/6-31G(d) optimized geometry is shown in Figure 1.

1

Figure 1. B3LYP/6-31G(d) optimized geometry of 1.

The ¹H NMR spectrum of 1 shows the bridgehead proton has only a small upfield shift (Δδ = 0.18ppm) relative that of 2. This suggests that both molecules have similar degrees of aromaticity/antiaromaticity, and since both molecules display large bond alternation (ΔR = 0.169 Å in 1 and 0.089 Å in 2) one can argue that both paratropic and diatropic ring currents are attenuated in both molecules. However, the NICS value of 1 is 10.6 ppm, indicative of considerable antiaromatic character, though this NICS value is much reduced from that in planar cyclooctatetraene constrained to the ring geometry of 1 (22.1 ppm). Rabinowitz and Komatsu argue that large HOMO-LUMO gap of 1 is responsible for the reduced antiaromatic character of 1.

Though not discussed in their paper, the aromatic stabilization (destabilization) energy of 1 can be computed. I took two approaches, shown in Reactions 1 and 2. The energies of the two reactions are -13.8 kcal mol^-1 for Reaction 1 and -3.4 kcal mol^-1 for Reaction 2. The large exothermicity of Reaction 1 reflects the strain of packing the four bicyclo moieties near each other, forcing the neighboring bridgehead hydrogens to be directed right at each other. The strain is better compensated in Reaction 2 by using 3 as the reference. Since 3 is of C₂ symmetry, some strain relief remains a contributor to the overall reaction energy. Thus it appears that if 1 is antiaromatic, if manifests in little energetic consequence.

Reaction 1

Reaction 2

References

(1) Nishinaga, T.; Uto, T.; Inoue, R.; Matsuura, A.; Treitel, N.; Rabinovitz, M.; Komatsu, K., "Antiaromaticity and Reactivity of a Planar Cyclooctatetraene Fully Annelated with Bicyclo[2.1.1]hexane Units," Chem. Eur. J., 2008, 14, 2067-2074, DOI: 10.1002/chem.200701405

InChIs

1: InChI=1/C24H24/c1-9-2-10(1)18-17(9)19-11-3-13(4-11)21(19)23-15-7-16(8-15)24(23)22-14-5-12(6-14)20(18)22/h9-16H,1-8H2/b19-17-,20-18-,23-21-,24-22-
InChIKey=PUZMOHQGDBIGOO-LEYBOLSUBU

2: InChI=1/C18H18/c1-7-2-8(1)14-13(7)15-9-3-11(4-9)17(15)18-12-5-10(6-12)16(14)18/h7-12H,1-6H2
InChIKey=ULLLVKXTLZQQFF-UHFFFAOYAL

3: InChI=1/C14H16/c1-7-9-3-11(4-9)13(7)14-8(2)10-5-12(14)6-10/h9-12H,1-6H2/b14-13-
InChIKey=CSIHJUFBXMYVBH-YPKPFQOOBF

The gas phase structure of the amino acids is in their canonical or neutral form, while their aqueous solution phase structure is zwitterionic. An interesting question is how many water molecules are needed to make the zwitterionic structure more energetically favorable than the neutral form. For glycine, it appears that seven water molecules are needed to make the zwitterion the favorable tautomer.^1,2

Arginine, on the other hand, appears to require only one water molecule to make the zwitterion lower in energy than the neutral form.³ The B3LYP/6-311++G** structures of the lowest energy neutral (1N) and zwitterion (1Z) cluster with one water are shown in Figure 1. The zwitterion is 1.68 kcal mol^-1 lower in energy. What makes this zwitterion so favorable is that the protonation occurs on the guanidine group, not on the amine group. The guanidine group is more basic than the amine. Further, the water can accept a proton from both nitrogens of the guanidine and donate a proton to the carboxylate group.

1N (1.68)

1Z (0.0)

Figure 1. B3LYP/6-311++G** structures and relative energies (kcal mol^-1) of the lowest energy arginine neutral (1N) and zwitterion (1Z) cluster with one water.³

References

(1) Aikens, C. M.; Gordon, M. S., "Incremental Solvation of Nonionized and Zwitterionic Glycine," J. Am. Chem. Soc., 2006, 128, 12835-12850, DOI: 10.1021/ja062842p.

(2) Bachrach, S. M., "Microsolvation of Glycine: A DFT Study," j. Phys. Chem. A, 2008, 112, 3722-3730, DOI: 10.1021/jp711048c.

(3) Im, S.; Jang, S.-W.; Lee, S.; Lee, Y.; Kim, B., "Arginine Zwitterion is More Stable than the Canonical Form when Solvated by a Water Molecule," J. Phys. Chem. A, 2008, 112, 9767-9770, DOI: 10.1021/jp801933y.

InChIs

1: InChI=1/C6H14N4O2/c7-4(5(11)12)2-1-3-10-6(8)9/h4H,1-3,7H2,(H,11,12)(H4,8,9,10)/f/h8,10-11H,9H2
InChIKey=ODKSFYDXXFIFQN-MYOKTFMPCK

I am grateful for another very nice review of my book Computational Organic Chemistry, this one appearing in Organic Process Research and Development written by Eddy M. E. Viseux: Org. Process Res. Dev., 2008, 12, 1313, DOI: 10.1021/op800178c.

Once again into the breach – how much strain can an aromatic species withstand and remain aromatic? Cyranski, Bodwell and Schleyer employ the [n](2,7)pyrenophanes 1 to explore this question.¹ As the tethering bridge gets shorter, the pyrene framework must pucker, presumably reducing its aromatic character. Systematic shrinking allows one to examine the loss of aromaticity as defined by aromatic stabilization energy (ASE), magnetic susceptibility exaltation (Λ) and NICS, among other measures.

They examined the series of pyrenophanes where the tethering chain has 6 to 12 carbon atoms. I have shown the structures of three of these compounds in Figure 1. The bend angle α is defined as the angle made between the outside ring plane and the horizon. Relative ASE is computed using Reaction 1, which cleverly avoids the complication of exactly (a) what is the ASE of pyrene itself and (b) what is the strain energy in these compounds.

1a	1d
1g

Figure 1. B3LYP/6-311G** optimized geometries of 1a, 1d, and 1g.¹

Reaction 1

The results of the computations for this series of pyrenophanes is given in Table 1. The bending angle smoothly increases with decreasing length of the tether. The ASE decreases in the same manner. The ASE correlates quite well with the bending angle, as does the relative magnetic susceptibility exaltation. The NICS(1) values become less negative with decreasing tether length.

Table 1. Computed values for the pyrenophanes.

All of these trends are consistent with reduced aromaticity with increased out-of-plane distortion of the pyrene framework. What may be surprising is the relatively small loss of aromaticity in this sequence. Even though the bend angle is as large as almost 40°, the loss of ASE is only 16 kcal mol^-1, only about a quarter of the ASE of pyrene itself. Apparently, aromatic systems are fairly robust!

References

(1) Dobrowolski, M. A.; Cyranski, M. K.; Merner, B. L.; Bodwell, G. J.; Wu, J. I.; Schleyer, P. v. R.,
"Interplay of π-Electron Delocalization and Strain in [n](2,7)Pyrenophanes," J. Org. Chem., 2008, 73, 8001-8009, DOI: 10.1021/jo8014159

InChIs

1a: InChI=1/C22H20/c1-2-4-6-16-13-19-9-7-17-11-15(5-3-1)12-18-8-10-20(14-16)22(19)21(17)18/h7-14H,1-6H2
InChIKey=SJCYSWGQWCIONQ-UHFFFAOYAF

1b: InChI=1/C23H22/c1-2-4-6-16-12-18-8-10-20-14-17(7-5-3-1)15-21-11-9-19(13-16)22(18)23(20)21/h8-15H,1-7H2
InChIKey=VHVKAELFYUXZEM-UHFFFAOYAW

1c: InChI=1/C24H24/c1-2-4-6-8-18-15-21-11-9-19-13-17(7-5-3-1)14-20-10-12-22(16-18)24(21)23(19)20/h9-16H,1-8H2
InChIKey=HXPWDTNIUQNKLV-UHFFFAOYAQ

1d: InChI=1/C25H26/c1-2-4-6-8-18-14-20-10-12-22-16-19(9-7-5-3-1)17-23-13-11-21(15-18)24(20)25(22)23/h10-17H,1-9H2
InChIKey=DWYMZJZWMFVOIR-UHFFFAOYAM

1e: InChI=1/C26H28/c1-2-4-6-8-10-20-17-23-13-11-21-15-19(9-7-5-3-1)16-22-12-14-24(18-20)26(23)25(21)22/h11-18H,1-10H2
InChIKey=PZBADGOJPAEUIK-UHFFFAOYAZ

1f: InChI=1/C27H30/c1-2-4-6-8-10-20-16-22-12-14-24-18-21(11-9-7-5-3-1)19-25-15-13-23(17-20)26(22)27(24)25/h12-19H,1-11H2
InChIKey=YVZIXELCLJHDLW-UHFFFAOYAO

1g: InChI=1/C28H32/c1-2-4-6-8-10-12-22-19-25-15-13-23-17-21(11-9-7-5-3-1)18-24-14-16-26(20-22)28(25)27(23)24/h13-20H,1-12H2
InChIKey=QDAMLTATWKFTFB-UHFFFAOYAF

Pyrene: InChI=1/C16H10/c1-3-11-7-9-13-5-2-6-14-10-8-12(4-1)15(11)16(13)14/h1-10H
InChIKey=BBEAQIROQSPTKN-UHFFFAOYAB

4,9-dimethylenepyrene: InChI=1/C18H12/c1-11-9-13-5-4-8-16-12(2)10-14-6-3-7-15(11)17(14)18(13)16/h3-10H,1-2H2
InChIKey=XAAPFSHIUHWWCM-UHFFFAOYAM

Singleton has taken another foray into the murky arena of “dynamic effects”, this time with the aim of trying to provide some guidance towards making qualitative product predictions.¹ He has examined four different Diels-Alder reaction involving two diene species, each of which can act as either the diene or dienophile. I will discuss the results of two of these reactions, namely the reactions of 1 with 2 (Reaction 1) and 1 with 3 (Reaction 2).

In the experimental studies, Reaction 1 yields only 4, while reaction 2 yields both products in the ratio 6:7 = 1.6:1. Standard transition state theory would suggest that there are two different transition states for each reaction, one corresponding to the 4+2 reaction where 1 is the dienophile and the other TS has 1 as the dienophile. Then one would argue that in Reaction 1, the TS leading to 4 is much lower in energy than that leading to 5, and for Reaction 2, the TS state leading to 6 lies somewhat lower in energy than that leading to 7.

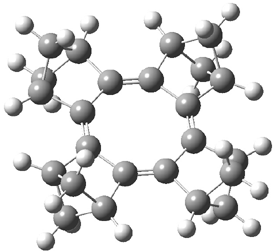
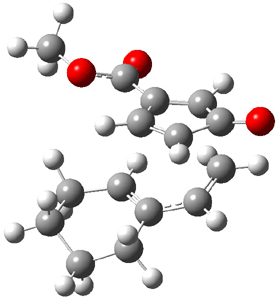
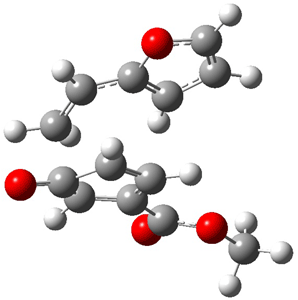
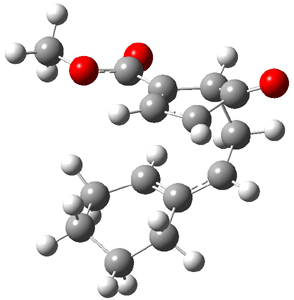
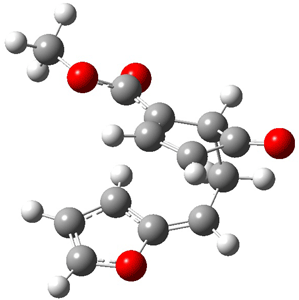
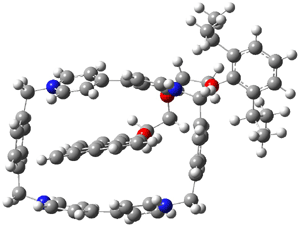
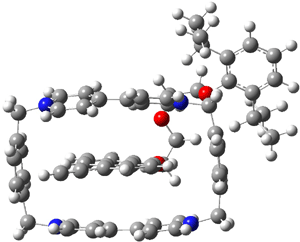
Now the interesting aspect of the potential energy surfaces for these two reactions is that there are only two transition states. The first corresponds to the Cope rearrangement between the two products (connecting 4 to 5 on the PES of Reaction 1 and 6 to 7 on the PES of Reaction 2). That leaves only one TS connecting reactants to products! These four TSs are displayed in Figure 1.

Reaction 1	Reaction 2
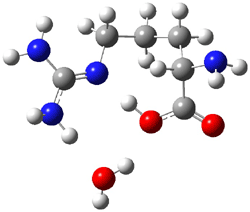
TS 12→45	TS 13→67
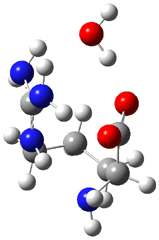
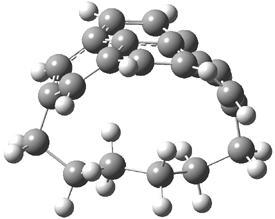
Cope TS 4→5	Cope TS 6→7

Figure 1. MPW1K/6-31+G** TSs on the PES of Reactions 1 and 2.¹

These transition states are “bispericyclic” (first recognized by Caramella²), having the characteristics of both possible Diels-Alder reactions, i.e. for Reaction 1 these are the [4π₁+2π₂] and [4π₂+2π₁]. What this implies is that the reactants come together, cross over a single transition states and then pass over a bifurcating surface where the lowest energy path (the IRC or reaction path) continues on to one product only. The second product, however, can be reached by passing over this same transition state and then following some other non-reaction path. This sort of surface is ripe for experiencing non-statistical behavior, or “dynamic effects”.

Trajectory studies were then performed to explore the product distributions. Starting from TS 12→45, 39 trajectories were followed: 28 ended with 4 and 10 ended with 5 while one trajectory recrossed the transition state. Isomerization of 5 into 4 is possible, and the predicted low barrier for this explains the sole observation of 4. For Reaction 2, of the 33 trajectories that originated at TS 13→67, 12 led to 6 and 19 led to 7. This distribution is consistent with the experimental product distribution of a slight excess of 7 over 6.

Once again we see here a relatively simple reaction whose product distribution is only interpretable using expensive trajectory computations, and the result leave little simplifying concepts to guide us in generalizing to other (related) systems. Singleton does provide two rules-of-thumb that may help prod us towards creating some sort of dynamic model. First, he notes that the geometry of the single transition state that “leads” to the two products can suggest the major product. The TS geometry can be “closer” to one product over the other. For example, in TS 12→45 the two forming C-C bonds that differentiate the two products are 2.95 and 2.99 Å, and the shorter distance corresponds to forming 4. In TS 13→67, the two C-C distances are 2.83 and 3.13 Å, with the shorter distance corresponding to forming 6. The second point has to do with the position of the second TS, the one separating the two products. This TS acts to separate the PES into two basins, one for each product. The farther this TS is from the first TS, the greater the selectivity.

As Singleton notes, neither of these points is particularly surprising in hindsight. Nonetheless, since we have so little guidance in understanding reactions that are under dynamic control, any progress here is important.

References

(1) Thomas, J. B.; Waas, J. R.; Harmata, M.; Singleton, D. A., "Control Elements in Dynamically Determined Selectivity on a Bifurcating Surface," J. Am. Chem. Soc. 2008, 130, 14544-14555, DOI: 10.1021/ja802577v.

(2) Caramella, P.; Quadrelli, P.; Toma, L., "An Unexpected Bispericyclic Transition Structure Leading to 4+2 and 2+4 Cycloadducts in the Endo Dimerization of Cyclopentadiene," J. Am. Chem. Soc. 2002, 124, 1130-1131, DOI: 10.1021/ja016622h

InChIs

1: InChI=1/C7H6O3/c1-10-7(9)5-2-3-6(8)4-5/h2-4H,1H3
InChIKey=XDEAUYSKQHEYSC-UHFFFAOYAM

2: InChI=1/C8H12/c1-2-8-6-4-3-5-7-8/h2,6H,1,3-5,7H2
InChIKey=SDRZFSPCVYEJTP-UHFFFAOYAI

3: InChI=1/C6H6O/c1-2-6-4-3-5-7-6/h2-5H,1H2
InChIKey=QQBUHYQVKJQAOB-UHFFFAOYAO

4: InChI=1/C15H18O3/c1-18-14(17)15-9-8-13(16)12(15)7-6-10-4-2-3-5-11(10)15/h6,8-9,11-12H,2-5,7H2,1H3/t1,12-,15+/m1/s1
InChIKey=IASNDVSMFFVIFJ-GDHFLIHABF

5: InChI=1/C15H18O3/c1-18-15(17)13-8-11-10(7-12(13)14(11)16)9-5-3-2-4-6-9/h5,8,10-12H,2-4,6-7H2,1H3
InChIKey=XOFSMKQRRVWZHS-UHFFFAOYAW

6: InChI=1/C13H12O4/c1-16-13(15)10-6-8-7(5-9(10)12(8)14)11-3-2-4-17-11/h2-4,6-9H,5H2,1H3
InChIKey=HTSLDILNKGZMHE-UHFFFAOYAH

7: InChI=1/C13H12O4/c1-16-12(15)13-6-4-10(14)8(13)2-3-11-9(13)5-7-17-11/h3-9H,2H2,1H3/t8-,9?,13-/m1/s1
InChIKey=URYPWPBQFGUBGW-KEJGKJRFBM

Host-guest recognition is a major theme of modern chemistry. Computation of these systems remains a real challenge for many reasons, especially the typically large size of the molecules involved and the need for accurately computing weak, non-covalent interactions. This latter point remains a major problem with density functional theory.

Goddard has now examined a rotaxane system.¹ Goddard employed a variety of functionals (B3LYP. PBE, and MO6 variants) to 1, a compound prepared by Stoddart.² The counterion of the experimentally prepared rotoxane is PF₆^–; in the computations, Goddrad employed either no counterions or four chloride ions.

The optimized structure of 1 without counterions computed at B3LYP/6-31G** and MO6-L/6-31G** are shown in Figure 1. The major difference in these structures is the orientation of the naphthyl group inside the host. B3LYP predicts that it is skewed, while MO6-L predicts that it lies parallel to the bipyridinium side. The x-ray structure has the parallel structure, similar to that found with MO6-L, though the pendant bis-i-proylphenyl ring is farther down in the x-ray structure than in the computed structure.

(a)

(b)

Figure 1. Optimized structure of 1⁴⁺
(a) B3LYP/6-31G** and (b) MO6-L/6-31G**.¹

None of the methods perform particularly well in computing the binding energy of the host and guest. The experimental value is -4.9 ± 1 kcal mol^-1. In the gas phase, the two methods predict that the system is bound, -24.9 (B3LYP, -75.2 kcal mol^-1, MO6-L). In acetonitrile, B3LYP predicts that it is unbound, while MO6-L predicts a binding energy of -27.5 kcal mol^-1. Inclusion of four chloride ions leads to some improvement in the binding energy in the gas phase but not for the solution phase.

The excitation energy is 3.50 eV.Computation of the excitation energy is poor with B3LYP (1.33 eV) but nearly exact with MO6-HF//MO6-L (3.42 eV).

Goddard concludes that computation of these sort of interlocked molecules should be performed with the MO6 family of functionals, but clearly more work is needed if accurate energies are required.

References

(1) Benitez, D.; Tkatchouk, E.; Yoon, I.; Stoddart, J. F.; Goddard, W. A., "Experimentally-Based Recommendations of Density Functionals for Predicting Properties in Mechanically Interlocked Molecules," J. Am. Chem. Soc., 2008, 130, 14928-14929, DOI: http://dx.doi.org/10.1021/ja805953u.

(2) Nygaard, S.; Leung, K. C. F.; Aprahamian, I.; Ikeda, T.; Saha, S.; Laursen, B. W.; Kim, S.-Y.; Hansen, S. W.; Stein, P. C.; Flood, A. H.; Stoddart, J. F.; Jeppesen, J. O., "Functionally Rigid Bistable [2]Rotaxanes," J. Am. Chem. Soc., 2007, 129, 960-970, DOI: http://dx.doi.org/10.1021/ja0663529

InChIs

Guest: InChI=1/C28H32O3/c1-6-22-10-7-14-26-25(22)13-9-15-27(26)30-18-16-29-17-19-31-28-23(20(2)3)11-8-12-24(28)21(4)5/h1,7-15,20-21H,16-19H2,2-5H3
InChIKey=HYRADSXCSHFXAZ-UHFFFAOYAJ

Host: InChI=1/C36H32N4/c1-2-30-4-3-29(1)25-37-17-9-33(10-18-37)35-13-21-39(22-14-35)27-31-5-7-32(8-6-31)28-40-23-15-36(16-24-40)34-11-19-38(26-30)20-12-34/h1-24H,25-28H2/q+4
InChIKey=URORLZXVTFVIPS-UHFFFAOYAV

Concern about the use of DFT for general use in organic chemistry remains high; see my previous posts (1, 2, 3). Houk has now examined the reaction enthalpies of ten simple Diels-Alder reactions using a variety of functionals in the search for the root cause of the problem(s).¹

The ten reactions are listed in Scheme 1, and involve cyclic and acyclic dienes and either ethylene or acetylene as the dienophile. Table 1 lists the minimum and maximum deviation of the DFT enthalpies relative to the CBS-QB3 enthalpies (which are in excellent accord with experiment). Clearly, all of the DFT methods perform poorly, with significant errors in these simple reaction energies. The exception is the MO6-2X functional, whose errors are only slightly larger than that found with the SCS-MP2 method. Use of a larger basis set (6-311+G(2df,2p)) reduced errors only a small amount.

Table 1. Maximum, minimum and mean deviation of reaction enthalpies (kcal mol^-1) for the reactions in Scheme 1 using the 6-31+G(d,p) basis set.¹

In order to discern where the problem originates, they next explore the changes that occur in the Diels-Alder reaction: two π bonds are transformed into one σ and one π bond and the conjugation of the diene is lost, leading to (proto)branching in the product. Reactions 1-3 are used to assess the energy consequence of converting a π bond into a σ bond, creating a protobranch, and the loss of conjugation, respectively.

The energies of these reactions were then evaluated with the various functionals. It is only with the conversion of the π bond into a σ bond that they find a significant discrepancy between the DFT estimates and the CBS-QB3 estimate. DFT methods overestimate the energy for the π → σ exchange, by typically around 5 kcal mol^-1, but it can be much worse. Relying on cancellation of errors to save the day for DFT will not work when these types of bond changes are involved. Once again, the user of DFT is severely cautioned!

References

(1) Pieniazek, S. N.; Clemente, F. R.; Houk, K. N., "Sources of Error in DFT Computations of C-C Bond Formation Thermochemistries: π → σ Transformations and Error Cancellation by DFT Methods," Angew. Chem. Int. Ed. 2008, 47, 7746-7749, DOI: 10.1002/anie.200801843