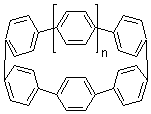
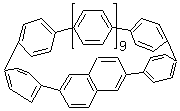
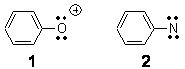Single-walled carbon nanotubes (SWNT) can be thought of as built from component macrocycles, often called nanohoops. So, for example, cycloparaphenylenes like 1 can be the thought of as the precursor (at least in principle) of armchair SWNTs. To create chiral SWNTs, Itami¹ has suggested that cycloparaphenylene-naphthalene (2) and other acene substituted macrocycles would serve as appropriate precursors.

Itami has synthesized 2 (having 13 phenyl groups and one naphthyl group) and also examined the ring strain energy and racemization energy of a series of these types of compounds at B3LYP/6-31G(d). As might be expected, based on studies of the cycloparaphenylenes themselves,^2,3 ring strain energy decreases with increasing size of the macrocycle. So, for example, the macrocycle with one naphthyl group and 5 phenyl rings has a strain energy of 90 kcal mol^-1, but the strain is reduced to 40 kcal mol^-1 with 13 phenyl rings.

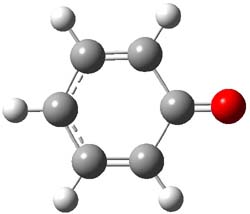
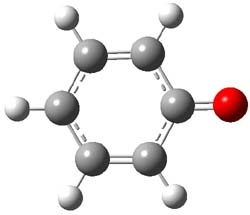
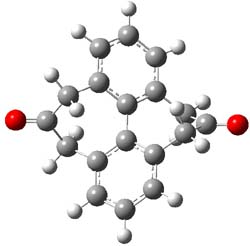
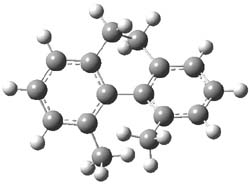
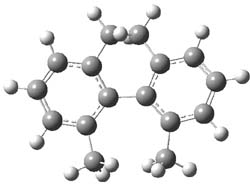
The macrocycle 2 and related structures are chiral, existing in P and M forms. The racemization involves first rotation of the naphthyl group, as shown in Figure 1, with a barrier of about 8 kcal mol^-1. The direct product has the opposite stereochemistry but is not in the lowest energy conformation. Rotations of some phenyl groups remains to occur, but these rotations are expected to have a barrier less than that for the rotation of the naphthyl group, based on the previous study of cycloparaphenylenes. Again, the racemization barrier decreases with the size of the macrocycle.

(P)-2	2-TS
(M)-2’

Figure 1. B3LYP/6-31G(d) optimized structures along the racemization pathway of 2.

References

(1) Omachi, H.; Segawa, Y.; Itami, K., "Synthesis and Racemization Process of Chiral Carbon Nanorings: A Step toward the Chemical Synthesis of Chiral Carbon Nanotubes," Org. Lett., 2011, 13, 2480-2483, DOI: 10.1021/ol200730m

(2) Segawa, Y.; Omachi, H.; Itami, K., "Theoretical Studies on the Structures and Strain Energies of Cycloparaphenylenes," Org. Lett., 2010, 12, 2262-2265, DOI: 10.1021/ol1006168

(3) Bachrach, S. M.; Stuck, D., "DFT Study of Cycloparaphenylenes and Heteroatom-Substituted Nanohoops," J. Org. Chem., 2010, 75, 6595-6604, DOI: 10.1021/jo101371m

InChIs

2: InChI=1/C88H58/c1-2-60-4-3-59(1)61-5-9-63(10-6-61)65-13-17-67(18-14-65)69-21-25-71(26-22-69)73-29-33-75(34-30-73)77-37-41-79(42-38-77)81-45-49-83(50-46-81)85-53-55-88-58-86(54-56-87(88)57-85)84-51-47-82(48-52-84)80-43-39-78(40-44-80)76-35-31-74(32-36-76)72-27-23-70(24-28-72)68-19-15-66(16-20-68)64-11-7-62(60)8-12-64/h1-58H/b61-59-,62-60-,65-63-,66-64-,69-67-,70-68-,73-71-,74-72-,77-75-,78-76-,81-79-,82-80-,85-83-,86-84+
InChIKey=VXOGKWSXPGSUSO-ZMOMEJFTBU

Saelli, Nicolaou, and Bagno point out in a recent article how the determination of the structure of vannusal B might have been guided by DFT computed ¹³C NMR chemical shifts, had they been available.¹ The original structure was proposed in 1999 as 1,² but was ultimately settled as 2 in 2010.³

The ¹³C NMR chemical shifts of 1 and 2 and some other alternatives were computed at M06/pcS-2//B3LYP/6-31g(d,p), where the pcS-2 basis set⁴ is one proposed by Jensen for computing chemical shifts. The computed chemical shifts of 1 poorly correlate with the experimental chemical shifts of vannusal B, with a low correlation coefficient of 0.9580 and a maximum error of 16.2 ppm. On the other hand, the correlation between the computed chemical shifts of 2 with the experimental values is excellent (R²=0.9948) and a maximum error of 3.0 ppm. Comparison of computed and experimental H-H coupling constants of model compounds of the “northeast” section of the molecule verified the correct structure is 2.

References

(1) Saielli, G.; Nicolaou, K. C.; Ortiz, A.; Zhang, H.; Bagno, A., "Addressing the Stereochemistry of Complex Organic Molecules by Density Functional Theory-NMR: Vannusal B in Retrospective," J. Am. Chem. Soc., 2011, 133, 6072-6077, DOI: 10.1021/ja201108a

(2) Guella, G.; Dini, F.; Pietra, F., "Metabolites with a Novel C30 Backbone from Marine Ciliates," Angew. Chem. Int. Ed., 1999, 38, 1134-1136, DOI: 10.1002/(SICI)1521-3773(19990419)38:8<1134::AID-ANIE1134>3.0.CO;2-U

(3) Nicolaou, K. C.; Ortiz, A.; Zhang, H.; Dagneau, P.; Lanver, A.; Jennings, M. P.; Arseniyadis, S.; Faraoni, R.; Lizos, D. E., "Total Synthesis and Structural Revision of Vannusals A and B: Synthesis of the Originally Assigned Structure of Vannusal B," J. Am. Chem. Soc., 2010, 132, 7138-7152, DOI: 10.1021/ja100740t

(4) Jensen, F., "Basis Set Convergence of Nuclear Magnetic Shielding Constants Calculated by Density Functional Methods," J. Chem. Theory Comput., 2008, 4, 719-727, DOI: 10.1021/ct800013z

InChI

vannusal B (2):
InChI=1/C31H46O5/c1-16(2)18-6-7-19(17(18)3)20-8-9-21-22(20)14-29(15-32)24-11-13-31(29,25(21)33)27(35)30(24)12-10-23(26(30)34)28(4,5)36/h14-15,17-21,23-27,33-36H,1,6-13H2,2-5H3/t17-,18+,19+,20+,21-,23+,24+,25+,26?,27+,29+,30-,31-/m1/s1
InChIKey=KYOBJLKAZYUEHK-GYGUSHOLBX

A significant portion of Chapter 4 of my book is devoted to phenylnitrene 2 and phenylcarbene. Phenyloxenium cation 1 is isoelectronic with phenylnitrene and so one might expect similar behavior of the two. Winter has reported a nice computational study of the singlet and triplet phenyloxenium cation and finds some very striking differences between phenyloxenium cation and phenylnitrene.¹

Phenylnitrene has a triplet ground state, with the ¹A₁ state about 18 kcal mol^-1 higher in energy, and the ¹A₂ state higher still. CASPT2/pVTZ//CASSCF(8,8)/pVTZ computations of 1 find the singlet ¹A₁ to be the ground state. The lowest triplet is 22.1 kcal mol^-1 higher in energy, and the lowest ¹A₁ state lies 30.8 kcal mol^-1 above the ground state singlet. (The structures of the lowest singlet and triplet of 1 are shown in Figure 1.) Reanalysis of the ultraviolet photoelectron spectrum of the phenoxy radical² switches the assignments of the observed transitions and is in excellent agreement with these computed values. G3 and CCSD(T)/cc-pVTZ predicts a similar value for the singlet-triplet gap. B3LYP, MPW1PW91, and some other DFT methods predict the singlet to be lower in energy than the triplet, but with a gap half of the correct value of 22 kcal mol^-1.

1 singlet (1A1)

1 triplet (3A2)

Figure 1. CASSCF(8,8) optimized geometries of the lowest singlet and triplet states of 1.

The origin of the difference between 1 and 2 lies in the description of the singlet state. The singlet state of 1 places the two lone pairs on oxygen into the sp-like orbital and into the in plane p orbital. However, in 2, the singlet is described by two determinants, one with the nitrogen lone pairs in the sp and in plane p orbital and the second determinant has them in the sp orbital and in the perpendicular p orbital. For 1, this single determinant allows for the positive charge to delocalize into the phenyl ring and off the very electronegative oxygen; this is manifest in a short C-O bond (1.211 Å). The greater electronegativity of oxygen then nitrogen brings the perpendicular p orbital lower in energy and better able to mix with the phenyl π-orbitals. In other words, the greater electronegativity of O over N results in a large symmetry break of the degenerate p orbitals.

References

(1) Hanway, P. J.; Winter, A. H., "Phenyloxenium Ions: More Like Phenylnitrenium Ions than Isoelectronic Phenylnitrenes?," J. Am. Chem. Soc., 2011, 133, 5086-5093, DOI: 10.1021/ja1114612

(2) Dewar, M. J. S.; David, D. E., "Ultraviolet photoelectron spectrum of the phenoxy radical," J. Am. Chem. Soc., 1980, 102, 7387-7389, DOI: 10.1021/ja00544a050

Lash has synthesized the simplified component of a porphyrin 1, which lacks two of the pyrrole rings.¹ This compound should act as a modified [18]annulene, and the NMR and x-ray structure support that notion. The NMR shows a multiplet at -2.52 ppm for the internal protons and the external protons show up at 9.88 and 9.96 ppm. The x-ray structure exhibits a nearly planar structure, with the C-C distances around the macrocycle varying from 1.379 to 1.418 Å. Interestingly, the UV-vis of 1shows a Soret-band at 401 nm, indicative of porphyrin-like behavior.

It is a simple thing to do some computations on a model of 1, and so I have computed (at B3LYP/6-311+G(d,p)) the structure and NMR of 2, shown in Figure 1. This compound is strictly planar. The C-C distances about the macrocycle vary from 1.386 to 1.415 Å, in excellent agreement with the experiment and indicating little bond alternation. The NICS values at the center of the macrocycle and 1 Å above this point are -12.6 and -11.9 ppm, supporting the aromatic [18]annulene structure. Further, the chemical shifts of the interior and exterior protons are computed to be -7.6 (interior) and 11.4 ppm (exterior) – in fair agreement with experiment. Nonetheless, simple computations provide support for the notion that this compound, and related porphyrins have a dominant [18]annulene character.

2

Figure 1. B3LYP/6-311+G(d,p) optimized structure of 2.

References

(1) Lash, T. D.; Jones, S. A.; Ferrence, G. M., "Synthesis and Characterization of Tetraphenyl-21,23-dideazaporphyrin: The Best Evidence Yet That Porphyrins Really Are the [18]Annulenes of Nature," J. Am. Chem. Soc., 2010, 132, 12786-12787, DOI: 10.1021/ja105146a

InChIs

1: InChI=1/C44H32N2/c1-2-18-30-38-42(34-23-11-6-12-24-34)44(36-27-15-8-16-28-36)40(46-38)32-20-4-3-19-3
1-39-43(35-25-13-7-14-26-35)41(37(45-39)29-17-1)33-21-9-5-10-22-33/h1-32H/b2-1-,4-3-,17-1+,18-2+,19-3+,20-4+,29-17+,30-18+,31-19+,32-20+,37-29-,38-30-,39-31-,40-32-
InChIKey=SOKXIWMGPPRDDE-VZLTUNCZBQ

2: InChI=1/C20H16N2/c1-2-6-10-18-15-16-20(22-18)12-8-4-3-7-11-19-14-13-17(21-19)9-5-1/h1-16H/b2-1-,4-3-,5-1+,6-2+,7-3+,8-4+,9-5+,10-6+,11-7+,12-8+,17-9-,18-10-,19-11-,20-12-
InChIKey=IWCJELFJBPNKQF-ICIIEBMOBH

Kinetic isotope effects (KIE) are a valuable tool for probing mechanisms without changing the potential energy surface. Their interpretation can sometimes be difficult – for example is a perdeutero group larger or smaller than the perhydro analogue?

O’Leary, Rablen and Meyer have examined two related molecules and their KIEs relating to stereoinversion.¹ 1 exhibits a normal isotope effect (k_H/k_D = 1.06) while 2 has an inverse isotope effect (k_H/k_D = 0.880). They optimized the structures and transition states (see Figure 1) for racemization of both compounds at B3LYP and MP2, and computed isotope effects based on the Biegeleisen-Mayer equation (which is based on reduced partition functions). The KIEs obtained from the two computational methods is very similar.

1	1TS
2	2TS

Figure 1. MP2/6-31G(d,p) optimized geometries of 1 and 2 and the transition states for their racemization.

The experimental and computed KIEs are listed in Table 1. The agreement between experiment and computation is excellent – suggesting that computations should be routinely employed when analyzing isotope effects.

Table 1. Experimental and computed KIEs for racemization of 1 and 2.

The authors decompose the isotope effects into enthalpic and entropic components and note that the interplay between these two can be subtle – sometimes one might dominate and other times the second term will dominate, and the terms can be cooperative or non-cooperative.

References

(1) O’Leary, D. J.; Rablen, P. R.; Meyer, M. P., "On the Origin of Conformational Kinetic Isotope Effects," Angew. Chem. Int. Ed., 2011, 50, 2564-2567, DOI: 10.1002/anie.201007322

InChIs

1: InChI=1/C18H14O2/c19-15-7-11-3-1-4-12-8-16(20)10-14-6-2-5-13(9-15)18(14)17(11)12/h1-6H,7-10H2
InChIKey=DYZSIUYFWKNLHS-UHFFFAOYAB

d₈–1: InChI=1/C18H14O2/c19-15-7-11-3-1-4-12-8-16(20)10-14-6-2-5-13(9-15)18(14)17(11)12/h1-6H,7-10H2/i7D2,8D2,9D2,10D2
InChIKey=DYZSIUYFWKNLHS-UFBJYANTEO

2: InChI=1/C16H18/c1-11-5-3-7-13-9-10-14-8-4-6-12(2)16(14)15(11)13/h3-8,13,15H,9-10H2,1-2H3
InChIKey=OBRIKDRTDGHGIQ-UHFFFAOYAU