Peter Vollhardt and Ken Houk have teamed up on an interesting account of pericyclic reactions of molecules related to starphenylene.¹ This touches on the nature of aromatic compounds and pericyclic reaction mechanisms, topics I take up in a few places in the book.

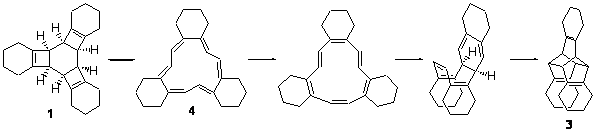
Compound 1 rearranges at 120 °C to 3, and the presumed pathway is
through 2 – the simultaneous [2+2+2] ring opening through the all-disrotatory path.
However, the computed (B3LYP/6-31G(d) activation energy is 34.6 kcal mol^-1 for this path, much higher than the experimental activation enthalpy, which is 28.9 kcal mol^-1.

The alternative path is to sequential break the cyclobutene rings with the standard conrotatory stereochemistry. This would give 4 and the barrier is 32.5 kcal mol^-1, in better agreement with experiment. From here, there is a bond shift, which traverses a Möbius geometry – as proposed by Karney and Castro (see the book and also this previous post). An electrocylization, followed by a Diels-Alder cycloaddition completes the path to 3. The rate determining step is the first: 1 ↔ 4.

On the other hand, upon heating 5 produces 6. Here the computed barrier for the [2+2+2] reaction (32.6 kcal mol^-1) is in nice agreement with the experimental value (34.1 kcal mol^-1), while the stepwise pathway has a much higher barrier (39.9 kcal mol^-1). They did not locate the polycyclic analogue of 3 (namely, 7) in the reaction of 5. This may be due in part to the fact that the bond shift is accompanied by a loss of aromaticity.

References

(1) Eichberg, M. J. H., K. N.; Lehmann, J.; Leonard, P. W.; Märker, A.; Norton, J. E.; Sawicka, D.; Vollhardt, K. P. C. W., G. D.; Wolff, S., "The Thermal Retro[2+2+2] cycloaddition of Cyclohexane Activated by Triscyclobutenannelation: Concerted All-Disrotatory versus Stepwise Conrotatory Pathways to Fused [12]Annulenes," Angew. Chem. Int. Ed., 2007, 46, 6894-6898, DOI: 10.1002/anie.200702474

InChIs

1: InChI=1/C24H30/c1-2-8-14-13(7-1)19-20(14)22-17-11-5-6-12-18(17)24(22)23-16-10-4-3-9-15(16)21(19)23/h19-24H,1-12H2/t19-,20+,21-,22+,23-,24+

2: InChI=1/C24H30/c1-2-8-20-15-16-22-10-5-6-12-24(22)18-17-23-11-4-3-9-21(23)14-13-19(20)7-1/h13-18H,1-12H2/b14-13-,16-15-,18-17-,19-13-,20-15+,21-14+,22-16+,23-17+,24-18-

3: InChI=1/C24H30/c1-2-8-14-13(7-1)19-21-15-9-3-4-10-16(15)22-20(14)23(19)17-11-5-6-12-18(17)24(21)22/h19-24H,1-12H2

4: InChI=1/C24H30/c1-2-8-20-15-16-22-10-5-6-12-24(22)18-17-23-11-4-3-9-21(23)14-13-19(20)7-1/h13-18H,1-12H2/b14-13+,16-15+,18-17+,19-13-,20-15+,21-14+,22-16-,23-17-,24-18+

5: InChI=1/C24H18/c1-2-8-14-13(7-1)19-20(14)22-17-11-5-6-12-18(17)24(22)23-16-10-4-3-9-15(16)21(19)23/h1-12,19-24H/t19-,20+,21-,22+,23-,24+

6: InChI=1/C24H18/c1-2-8-20-15-16-22-10-5-6-12-24(22)18-17-23-11-4-3-9-21(23)14-13-19(20)7-1/h1-18H/b14-13-,16-15-,18-17-,19-13-,20-15+,21-14+,22-16+,23-17+,24-18-

7: InChI=1/C24H18/c1-2-8-14-13(7-1)19-21-15-9-3-4-10-16(15)22-20(14)23(19)17-11-5-6-12-18(17)24(21)22/h1-12,19-24H

Cramer and Hoye have applied DFT computations to the predictions of both protons and carbon NMR chemical shifts in penam β-lactams¹ using the procedure previously described in my blog post Predicting NMR chemical shifts. They examined the compounds 1-8 by optimizing low energy conformers at B3LYP/6-31G(d) with IEFPCM (solvent=chloroform). The chemical shifts were then computed using these geometries with the larger 6-311+G(2d,p) basis set and four different functionals: B3LYP, PBE1 and the two specific functionals designed to produce proton and carbon chemical shifts: WP04 and WC04.

A number of interesting results are reported. First, all three functionals do a fine job in predicting the proton chemical shifts of 1-8, with WP04 slightly better than the other two.On the other hand, all three methods fail to predict the carbon chemical shifts of 1-3, though B3LYP and PBE1 do correctly identify 5-8. The failure of WC04 is surprising, especially since dimethyl disulfide was used in the training set. They also noted that WP04 using just the minimum energy conformation (as opposed to a Boltzmann averaged chemical shift sampled from many low energy conformers) did correctly identify lactams 1-4. This is helped by the fact that the lowest energy conformer constituted anywhere form 37% to 68% of the energy-weighted population.

References

(1) Wiitala, K. W.; Cramer, C. J.; Hoye, T. R., “Comparison of various density functional methods for distinguishing stereoisomers based on computed ¹H or ¹³C NMR chemical shifts using diastereomeric penam ?-lactams as a test set,” Mag. Reson. Chem., 2007, 45, 819-829, DOI: 10.1002/mrc.2045.

InChIs

1: InChI=1/C18H17NO5S/c1-18(2)14(17(23)24-3)19-15(22)11(16(19)25-18)10-12(20)8-6-4-5-7-9(8)13(10)21/h4-7,10-11,14,16H,1-3H3/t11-,14+,16+/m0/s1

5: InChI=1/C17H15NO5S/c1-17(2)13(16(22)23)18-14(21)10(15(18)24-17)9-11(19)7-5-3-4-6-8(7)12(9)20/h3-6,9-10,13,15H,1-2H3,(H,22,23)/t10-,13+,15+/m0/s1

Schleyer and Houk¹ offer a provocative paper examining the reference compounds that one chooses when trying to evaluate such concepts as ring strain energy and aromaticity. I discuss this at length in Chapter 2 of the book, focusing on the isodesmic, homodesmotic, and group equivalent reactions.

Their work starts with the isodesmic reaction

CH₃CH₂CH₃ + CH₄ → 2 CH₃CH₃

and note that this reaction is endothermic by 2.83 kcal mol^-1. They argue that 1,3-dialkyl interactions are stabilizing, and call this effect “protobranching”.

Gronert^2,3 has recently described the counterargument – that 1,3-dialkyl groups are repulsive – but whether the interaction is attractive or repulsive is not my concern here. Let’s proceed assuming that protobranching is in fact stabilizing.

Schleyer and Houk demonstrate that the stabilization of protobranching is nicely additive. In Table 1 are simple bond separation (isodesmic) reactions of straight-chain alkanes and cycloalkanes. This can then be extended to argue for why branched alkanes are more stable than their straight-chain analogues – namely, branched chains have more 1,3-dialkyl interactions and these are stabilizing. They note that the group separation reaction of iso-butane is more endothermic than that of pentane, yet the difference is neatly ascribed to protobranching.

Table 1. Energy of reactions and energy per protobranch (PB) using experimental heats of formation.

Now the interesting aspect is when this concept of protobranching is applied to ring systems. The conventional (homodesmotic) reaction for cyclopropane is

(CH₂)₃ + 3 C₂H₆ → 3 CH₃CH₂CH₃ ΔH = -27.7 kcal mol^-1

Schleyer and Houk argue that protobranching is not balanced in this reaction, and the consequence is that since propane is stabilized by about 2.8 kcal mol^-1, the reaction energy should be reduced by 8.4 kcal mol^-1. Thus the ring strain energy (RSE) of cyclopropane is 19.3 kcal mol^-1. This is essentially the value obtained when one employs the isodesmic reaction to evaluate the RSE of cyclopropane, namely

(CH₂)₃ + 3 CH₄ → 3 C₂H₆ ΔH = -19.2 kcal mol^-1

And this isodesmic reaction has balanced protobrancing (none!) on both sides. The reaction that balances protobranching (two on each side) for obtaining the RSE of cyclobutane is

(CH₂)₄ + 2 CH₄ → 2 CH₃CH₂CH₃ ΔH = -21.0 kcal mol^-1

Protobranching corrections need also be made to the question of aromatic stabilization energy or resonance energy of benzene. For example, since cyclohexane is invoked as one of the reference compounds in the following reaction, the resulting energy must be corrected for six protobranching interactions.

2 C₂H₄ + (CH₂)6 → (CH)₆ + 3 C₂H₆

The question now becomes “Is protobranching real and do we need to correct for it?” Further studies should be performed.

References

(1) Wodrich, M. D.; Wannere, C. S.; Mo, Y.; Jarowski, P. D.; Houk, K. N.; Schleyer, P. v. R., "The Concept of Protobranching and Its Many Paradigm Shifting Implications for Energy Evaluations," Chem. Eur. J. 2007, 13, 7731-7744, DOI: 10.1002/chem.200700602

(2) Gronert, S., "Evidence that Alkyl Substitution Provides Little Stabilization to Radicals: The C-C Bond Test and the Nonbonded Interaction Contradiction," J. Org. Chem., 2006, 71, 7045-7048, DOI: 10.1021/jo060797y.

(3) Gronert, S., "An Alternative Interpretation of the C-H Bond Strengths of Alkanes," J. Org. Chem., 2006, 71, 1209-1219, DOI: 10.1021/jo052363t.

The Highlights article¹ in a recent issue of Angewandte Chemie Intermational Edition concerns the induced chirality of an achiral solvent by a chiral solute determining the overall optical activity. I blogged on this in my last post. This Highlights article stressed (as I did) the novelty of this effect and the need for further experiments and computation. I am sure that more will come in this exciting area.

It is also interesting to me that Angewandte would feature in this way one of its own articles. Isn’t the fact that it was accepted and then published in the journal sufficient stamp of its novelty and importance? Can anyone say “nepotism”?

References

(1) Neugebauer, J., “Induced Chirality in Achiral Media – How Theory Unravels Mysterious Solvent Effects,” Angew. Chem. Int. Ed., 2007, 46, 7738-7740, DOI: 10.1002/anie.200702858.

Bertran and Wipf have examined the role of solvent organization about a chiral molecule in producing the optical activity.¹ They generated 1000 configurations of benzene arrayed about methyloxirane from a Monte Carlo simulation. Each configuration was then constructed by keeping every benzene molecules within 0.5 nm from the center-of-mass of methyloxirane, usually 8-10 solvent molecules. The optical rotation was then computed at four wavelengths using TDDFT at BP86/SVP. (The authors note that though the Gaussian group recommends B3LYP/aug-ccpVDZ,^2-4 using the non-hybrid functional allows the use of resolution-of–the-identity⁵ techniques that make the computations about six orders of magnitude faster – of critical importance given the size of the clusters and the sheer number of them!) Optical rotation is then obtained by averaging over the ensemble.

The computed optical rotations disagree with the experiment by about 50% in magnitude but have the correct sign across the four different wavelengths. Use of the COSMO model (implicit solvent) provides the wrong sign at short wavelengths. But perhaps most interesting is that the computed optical activity of the solvent molecules in the configuration about the solute, but without including methyloxirane, is nearly identical to that of the whole cluster! In other words, the optical activity is due to the dissymmetric distribution of the solvent molecules about the chiral molecule, not the chiral molecule itself! It is the imprint of the chiral molecule on the solvent ordering that accounts for nearly all of the optical activity.

References

(1) Mukhopadhyay, P.; Zuber, G.; Wipf, P.; Beratan, D. N., "Contribution of a Solute’s
Chiral Solvent Imprint to Optical Rotation," Angew. Chem. Int. Ed. 2007,
46, 6450-6452, DOI: 10.1002/anie.200702273

(2) Stephens, P. J.; McCann, D. M.; Cheeseman, J. R.; Frisch, M. J., "Determination of
absolute configurations of chiral molecules using ab initio time-dependent Density Functional Theory calculations of optical rotation: How reliable are absolute configurations obtained for molecules with small rotations?," Chirality 2005, 17, S52-S64, DOI: 10.1002/chir.20109.

(3) Stephens, P. J.; Devlin, F. J.; Cheeseman, J. R.; Frisch, M. J., "Calculation of Optical Rotation Using Density Functional Theory," J. Phys. Chem. A 2001, 105, 5356-5371, DOI: 10.1021/jp0105138.

(4) Stephens, P. J.; McCann, D. M.; Devlin, F. J.; Flood, T. C.; Butkus, E.; Stoncius,
S.; Cheeseman, J. R., "Determination of Molecular Structure Using Vibrational Circular Dichroism Spectroscopy: The Keto-lactone Product of Baeyer-Villiger Oxidation of (+)-(1R,5S)-Bicyclo[3.3.1]nonane-2,7-dione," J. Org. Chem. 2005, 70, 3903-3913, DOI: 10.1021/jo047906y.

(5) Eichkorn, K.; Treutler, O.; Ohm, H.; Haser, M.; Ahlrichs, R., "Auxiliary Basis Sets to Approximate Coulomb Potentials," Chem. Phys. Lett. 1995, 240, 283-289, DOI: 10.1016/0009-2614(95)00621-A.

In 2001, Pophristic and Goodman¹ initiated a controversy over the nature of the rotational barrier in ethane. Most organic textbooks argue that the barrier is due to unfavorable steric interactions in the eclipsed conformation. The Nature paper argues rather that the staggered conformation is favored due to hyperconjugative interactions between the C-H bond orbital on one methyl interacting with the anti-disposed antibonding C-H orbital of the other methyl group. Schreiner² wrote a follow-up essay where he was surprised by the response to this paper since he thought that the hyperconjugative explanation had been well-accepted within the community.

Now we have a nice review article by Mo and Gao³ that summarizes their recent investigation of the rotational barrier of ethane. Their main approach is to take advantage of the block localization method. Essentially, the methyl e-orbitals are localized to each methyl group, forbidding any hyperconjugation with each other. The energy difference then between the fully relaxed ethane and the block localized energy accounts for hyperconjugation – and this is about 0.76 kcal/mol, or about 25% of the barrier. The most important contributing factor to the barrier is the steric component – this is estimated by comparing the energies of the staggered and eclipsed conformers while freezing the π-like orbitals and removing the hyperconjugation effects. The estimate for the steric component is 2.73 kcal/mol. Mo and Gao conclude that the simple, traditional explanation, namely that steric interactions destabilize the eclipsed conformation, is in fact correct.

References

(1) Pophristic, V.; Goodman, L., "Hyperconjugation not Steric Repulsion leads to the Staggered Structure of Ethane," Nature 2001, 411, 565-568, DOI: 10.1038/35079036.

(2) Schreiner, P. R., "Teaching the Right Reasons: Lessons from the Mistaken Origin of the Rotational Barrier in Ethane," Angew. Chem. Int. Ed. 2002, 41, 3579-3582, DOI: 10.1002/1521-3773(20021004)41:19<3579::AID-ANIE3579>3.0.CO;2-S

(3) Mo, Y.; Gao, J., "Theoretical Analysis of the Rotational Barrier of Ethane," Acc. Chem. Res., 2007, 40, 113-119, DOI: 10.1021/ar068073w