Feng, Müller and co-workers have prepared a bistetracene analogue 1.¹ This molecule displays some interesting features. While a closed shell Kekule structure can be written, a biradical structure results in more closed Clar rings, suggesting that perhaps the molecule is a ground state singlet biradical. The loss of NMR signals with increasing temperature along with an EPR signal that increases with temperature both support the notion of a ground state singlet biradical with a triplet excited state. The EPR measurement suggest as singlet-triplet gap of 3.4 kcal mol^-1.

The optimized B3LYP/6-31G(d,p) geometries of the biradical singlet and triplet states are shown in Figure 1. The singlet is lower in energy by 6.7 kcal mol^-1. The largest spin densities are on the carbons that carry the lone electron within the diradical-type Kekule structures.

singlet 1

triplet 1

Figure 1. B3LYP/6-31G(d,p) optimized geometries of the biradical singlet and triplet states of 1.

References

(1) Liu, J.; Ravat, P.; Wagner, M.; Baumgarten, M.; Feng, X.; Müllen, K. "Tetrabenzo[a,f,j,o]perylene: A Polycyclic Aromatic Hydrocarbon With An Open-Shell Singlet Biradical Ground State," Angew. Chem. Int. Ed. 2015, 54, 12442-12446, DOI: 10.1002/anie.201502657.

InChIs

1: InChI=1S/C62H56/c1-33-25-35(3)51(36(4)26-33)53-45-17-13-15-19-47(45)57-56-44-24-22-42(62(10,11)12)30-40(44)32-50-54(52-37(5)27-34(2)28-38(52)6)46-18-14-16-20-48(46)58(60(50)56)55-43-23-21-41(61(7,8)9)29-39(43)31-49(53)59(55)57/h13-32H,1-12H3
InChIKey=LPRMROONCKWUEJ-UHFFFAOYSA-N

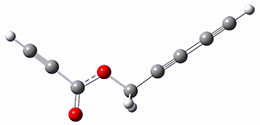
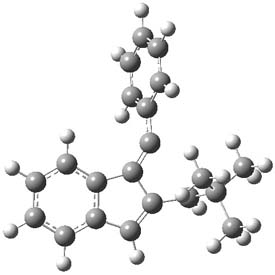
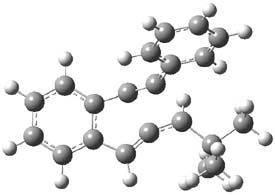
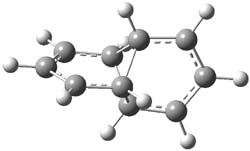
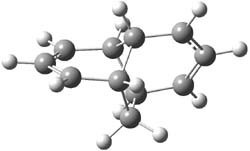
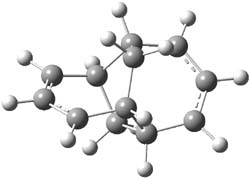
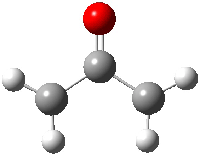
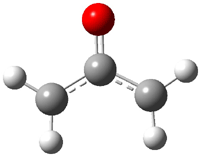
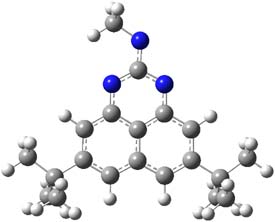
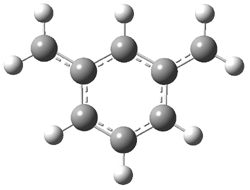
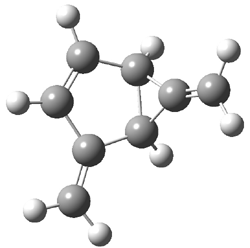
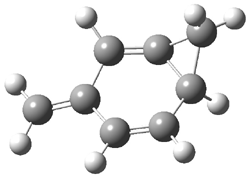
Cramer, Hoye, Kuwata and coworkers have examined the intramolecular cyclization of an alkyne with a diyne.¹ Their model system is 1, which can cyclize through a concerted transition state TSC togive the benzyne product 2, or it can proceed through a stepwise pathway, first going through TS1 to form the intermediate INT¸ before traversing through a second transition state TS2 and on to product 2. Using both computations and experiments, they examined a series of compounds with
differing substituents at the ends of the two yne moieties.

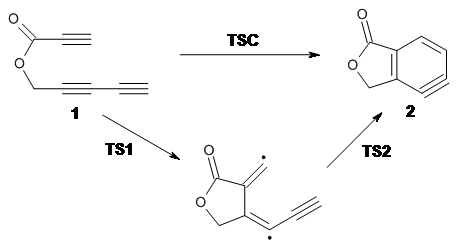
The experiments show almost the exact same rate of reaction regardless of the terminal substituents. This includes the parent case where the terminal substituents are hydrogens and also the case where the terminal substituents (which end up on adjacent centers on the benzyne ring) are bulky TMS groups. And though there is no real rate effect due to changes in solvent or the presence of light or triplet oxygen, which suggest a concerted reaction, these substituent effects argue for a step wise reaction.

SMD(o-dichlorobenzene)/B3LYP-D3BJ/6-311+G-(d,p)//M06-2X/6-311+G(d,p)
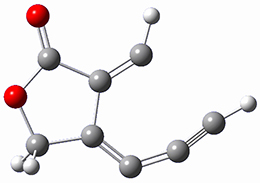
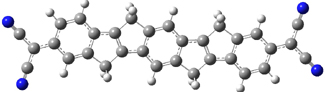
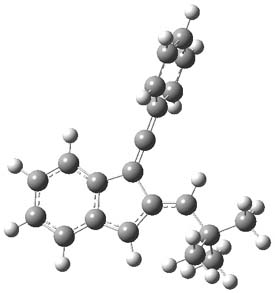
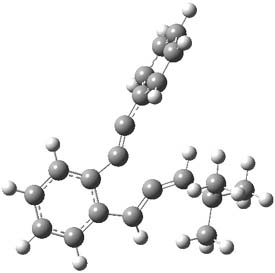
computations help explain these observations. Shown in Figure 1 are the optimized geometries and relative energies of the critical points on the reaction surface for the conversion of 1 into 2, and these results are similar with the other substituents as well.

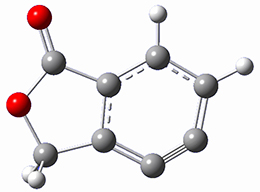
1 (0.0)	2 (-56.9)
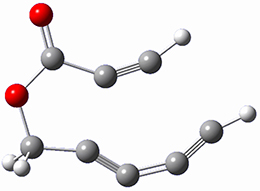
TSC (31.5)
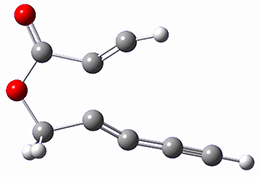
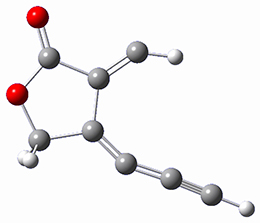
TS1 (25.5)	INT (18.8)
TS2 (18.1)

Figure 1. SMD(o-dichlorobenzene)/B3LYP-D3BJ/6-311+G-(d,p)//M06-2X/6-311+G(d,p) optimized geometries and relative energies (kcal mol^-1).

The first thing to note is that the concerted TSC is higher in energy than the stepwise TS1. The wavefunction for TSC unstable towards moving from a restricted to unrestricted formalism. Reoptimization of some of these concerted TSs actually led to the stepwise TS.

The next item of note is that TS2 for this case is actually lower in energy than the intermediate (this is a true TS on the energy surface, but when zero-point energy and other thermal corrections are included, it becomes lower in energy than INT). For some of the cases the second TS lies above the intermediate, but typically by a small amount.

Therefore, the mechanism of this reaction is stepwise, but the second step might have such a small barrier (or even no barrier) that one might consider this to be concerted, though highly asymmetric and really bearing little resemblance to more traditional concerted pericyclic reactions.

The authors obliquely hinted at some potential interesting dynamics. I suspect that molecular dynamics calculations will show no effect of that second TS, and one might observe some interesting dynamics, which could be seen in kinetic isotope experiments.

References

(1)  Marell, D. J.; Furan, L. R.; Woods, B. P.; Lei, X.; Bendelsmith, A. J.; Cramer, C. J.; Hoye, T. R.; Kuwata, K. T. "Mechanism of the Intramolecular Hexadehydro-Diels–Alder Reaction," J. Org. Chem. 2015 ASAP, DOI: 10.1021/acs.joc.5b01356.

InChIs

1: InChI=1S/C8H4O2/c1-3-5-6-7-10-8(9)4-2/h1-2H,7H2
InChIKey=MGXDIFXPYGGQLF-UHFFFAOYSA-N

2: InChI=1S/C8H4O2/c9-8-7-4-2-1-3-6(7)5-10-8/h2,4H,5H2
InChIKey=MYFORDRJCVOBTH-UHFFFAOYSA-N

Tsuji and Nakamura have prepared the tri-p­-quinodimethane 1.¹ Quinodimethanes are of interest because of their possible diradical character. This new example is most interesting. It is stable as a solid in air and ambient light for 6 months, or 2 months in solution. Its ESR shows fine structure, with a spin-spin distance estimated to be 14.6 Å, very close to the distance between the terminal carbons. The ground state is a singlet, with the triplet lying 2.12 kcal mol^-1 higher in energy.

Ar = 4-octylphenyl

UB3LYP/6-31G** computations (lacking the aryl and phenyl sidechains) indicate a ground state singlet (with sizable spin contamination) and a gap to the triplet of 1.83 kcal mol^-1. The computed geometry is shown in Figure 1.

1

Figure 1. UB3LYP/6-31G** optimized geometry of 1.

The analog having just two quinodimethane units showed no ESR signal and the computed singlet-triplet energy gap is 5.68 kcal mol^-1.

It would have been interesting to have computed the NICS values for the 6-member rings – as a measure of aromatic vs. non aromatic character to further support the participation of the biradical resonance structure contribution to 1.

References

(1) Zhu, X.; Tsuji, H.; Nakabayashi, K.; Ohkoshi, S.-i.; Nakamura, E., "Air- and Heat-Stable Planar Tri-p-quinodimethane with Distinct Biradical Characteristics," J. Am. Chem. Soc., 2011, 133, 16342-16345, DOI: 10.1021/ja206060n

InChI

1: InChI=1/C112H112N4/c1-5-9-13-17-21-29-41-81-53-63-93(64-54-81)111(94-65-55-82(56-66-94)42-30-22-18-14-10-6-2)101-73-85(87(77-113)78-114)61-71-97(101)105-107(111)99-75-104-100(76-103(99)109(105,89-45-33-25-34-46-89)90-47-35-26-36-48-90)108-106(110(104,91-49-37-27-38-50-91)92-51-39-28-40-52-92)98-72-62-86(88(79-115)80-116)74-102(98)112(108,95-67-57-83(58-68-95)43-31-23-19-15-11-7-3)96-69-59-84(60-70-96)44-32-24-20-16-12-8-4/h25-28,33-40,45-76H,5-24,29-32,41-44H2,1-4H3
InChIKey=IDOIPCRGROEZHG-UHFFFAOYAD

1 (lacking aryl side chains): InChI=1/C32H16N4/c33-13-23(14-34)17-1-3-25-19(5-17)9-31-27-8-22-12-30-26-4-2-18(24(15-35)16-36)6-20(26)10-32(30)28(22)7-21(27)11-29(25)31/h1-8H,9-12H2
InChIKey=JRLKUOJPPWAWTD-UHFFFAOYAN

Continuing their studies of ene-yne cyclizations, the Schmittel group examined the apparent [2+2] cyclization of the allene-yne 1.¹ They proposed that it first closed the diradical 2 and then in a second step the four-member ring is formed, giving 3.

Evidence supporting the intermediate diradical is that heating 1a in the presence of 1,4-cyclohexadiene gives 11% of the trapped species 4a. Interestingly, heating 1b gives 26% of 3b, while the reaction of 1c gives 72% of the ring closed product 3c.

Schmittel suggests the intermediate diradical 2b is planar, while 2c is not, and the radical centers are nicely position in the latter compound for quick closure to product.

UBLYP/6-31G(d) computations support the mechanism. The transition state taking 1b to 2b (TS1, shown in Figure 1) lies 20.2 kcal mol^-1 above reactant. The intermediate diradical 2b is 7.9 kcal mol^-1 above reactant 1b. The second transition state (TS2) for closing the four-member ring lies 27.8 kcal mol^-1 above reactant, making it the rate determining step. The overall reaction is exothermic by -12.4 kcal mol^-1. The transition state for a single step reaction, taking 1b directly into 3b (TS3) is very high, 49.0 kcal mol^-1 above 1b, and is therefore non-competitive with the stepwise pathway. These computations suggest a reversible formation of the intermediate, followed by a rate limiting step to making the four-member ring, completely consistent with the experiments.

2b
TS1	TS2
TS3

Figure 2. UBLYP/6-31G(d) optimized structures of 2b, TS1, TS2, and TS3.

References

1) Cinar, M. E.; Vavilala, C.; Fan, J.; Schmittel, M., "The thermal C²-C⁶/[2 + 2] cyclisation of enyne-allenes: Reversible diradical formation," Org. Biomol. Chem. 2011, 9, 3776-3779, DOI: 10.1039/C0OB01275K

InChIs

1b: InChI=1/C21H20/c1-21(2,3)17-9-14-19-12-7-8-13-20(19)16-15-18-10-5-4-6-11-18/h4-8,10-14,17H,1-3H3/t9-/m0/s1
InChIKey=HRQIWBDQUVQGEK-VIFPVBQEBW>

3b: InChI=1/C21H20/c1-21(2,3)20-17-13-15-11-7-8-12-16(15)19(17)18(20)14-9-5-4-6-10-14/h4-13,20H,1-3H3
InChIKey=GKHJKEWSMNKHEN-UHFFFAOYAW

Interacting bis-allyl radicals are the topic of a computational study by Gleiter and Borden.¹ The new twist is to have the two allyl groups interact through a cyclobutyl, cyclopentyl or cyclohexyl ring, as in 1-3.

The degree of interaction of the radical electrons is evaluated with a number of metrics. First, the singlet-triplet energy gap is computed at CASSCF(6,6)/6-31G(d) and UB3LYP/6-31G(d). A larger gap is suggestive of strong interaction between the two allyl radicals. Next, the <S²> value of the UB3LYP wavefunction will be 0 for a pure singlet, which occurs when the radicals are strongly interacting. A value near 1 suggests an electron localized into each allyl fragment. Lastly, the natural orbital occupation numbers (NOON) of the two highest lying orbitals would be 2 and 0 for the pure interacting state and each would be 1 for the non-interacting state. The B3LYP/6-31G(d) optimized geometries of 1-3 are shown in Figure 1. The values of each metric are listed in Table 1.

1	2
3

Figure 1. B3LYP/6-31G(d) optimized geometries of 1-3.

Table 1. Metrics for evaluating the allyl interaction in 1-3.

The different metrics are all consistent. The allyl radicals are strongly interacting in 1, with a low lying singlet state. The interaction is significantly lessened in 2 and smaller still in 3. The authors argue these differences in terms of the molecular orbital interactions between the allyl fragments and the central ring fragment.

References

(1) Lovitt, C. F.; Dong, H.; Hrovat, D. A.; Gleiter, R.; Borden, W. T., "Through-Bond Interactions in the Diradical Intermediates Formed in the Rearrangements of Bicyclo[n.m.0]alkatetraenes," J. Am. Chem. Soc., 2010, 132, 14617-14624, DOI: ja106329t

InChIs

1: InChI=1/C10H10/c1-3-7-9-5-2-6-10(7)8(9)4-1/h1-10H
InChIKey=QQZALYREQJSRLB-UHFFFAOYAA

2: InChI=1/C11H12/c1-3-8-7-9-4-2-6-11(8)10(9)5-1/h1-6,8-11H,7H2
InChIKey=XHSRXRHTBHVJQX-UHFFFAOYAV

3: InChI=1/C12H14/c1-3-9-7-12-6-2-5-11(9)8-10(12)4-1/h1-6,9-12H,7-8H2
InChIKey=JFNCWTOWDGQJLS-UHFFFAOYAA

The longstanding unknown oxyallyl diradical (1) singlet-triplet gap has now been addressed with a very nice photoelectron spectroscopy study by Lineberger with interpretation greatly aided by computations provided by Hrovat and Borden.¹

The photoelectron detachment spectrum of oxyallyl radical anion shows 5 major peaks, one at 1.942 eV and a series of four peaks starting at 1.997 eV separated by 405 cm^-1.

B3LYP/6-311++G(d,p) computations indicate that the energy for electron detachment from the radical anion to triplet oxyallyl diradical is 1.979 eV. (The structure of triplet 1 is shown in Figure 1.) Further, the computed vibrational frequency of the C-C-C bend is 408 cm^-1. These computations suggest that the four peak sequence represents a vibrational progression in the C-C-C bend of the triplet oxyallyl diradical.

1A1

3B2

Figure 1. Structures of the singlet and triplet oxyallyl diradical 1.¹

CASPT2 computations on singlet oxyallayl diradical indicate that it lies in a very shallow well, lower than the zero-point energy. (This structure is shown in Figure 1.) In fact, the singlet diradical can collapse without a barrier to cyclopropanone. Interestingly, the C-O stretching frequency of 1 is computed to be 1731 cm^-1, and close inspection of the photoelectron spectrum does show a progression of this magnitude originating from peak A. Therefore, both the singlet and triplet states of 1 are identified and their gap is extraordinarily small – the singlet is only 0.055 eV lower in energy than the triplet.

References

(1) Ichino, T.; Villano, S. M.; Gianola, A. J.; Goebbert, D. J.; Velarde, L.; Sanov, A.; Blanksby, S. J.; Zhou, X.; Hrovat, D. A.; Borden, W. T.; Lineberger, W. C., "The Lowest Singlet and Triplet States of the Oxyallyl Diradical," Angew. Chem. Int. Ed., 2009, 48, 8509-8511, DOI: 10.1002/anie.200904417

I missed this when it came out, but Quast, Sander and Borden have made the very interesting non-Kekule diradical 1.¹

³1

The EPR spectra shows the characteristic six-line signal, with zero-field splitting parameters consistent with related triplet diradicals. The Curie-Weiss plot is linear from 4.6 to 22.9 K. These data suggest a triplet ground state. CASSCF(14,14)/6-31G* computations indicate that the triplet lies 8.5 kcal mol^-1 below the singlet. The optimized triplet geometry is shown in Figure 1. The triplet ground state is consistent with the Borden-Davidson rules for radicals.²

31

Figure 1. CASSCF(14,14)/6-31G* optimized structure of triplet 1.

References

(1) Quast, H.; Nudling, W.; Klemm, G.; Kirschfeld, A.; Neuhaus, P.; Sander, W.; Hrovat, D. A.; Borden, W. T., "A Perimidine-Derived Non-Kekule Triplet Diradical," J. Org. Chem. 2008, 73, 4956-4961, DOI: 10.1021/jo800589y.

(2) Borden, W. T.; Davidson, E. R., "Effects of electron repulsion in conjugated hydrocarbon diradicals," J. Am. Chem. Soc. 1977, 99, 4587-4594, DOI: 10.1021/ja00456a010.

InChIs

1: InChI=1/C20H27N3/c1-19(2,3)13-8-12-9-14(20(4,5)6)11-16-17(12)15(10-13)22-18(21-7)23-16/h8-11H,1-7H3,(H2,21,22,23)/f/h22-23H
InChIKey=XAKUHDACNAUAAB-PDJAEHLQCL

The photochemistry of m-xylylene 2 has been studied by Sander¹ and, as might be anticipated, it’s fascinating! Flash vapor pyrolysis of 1 produces 2. Photolysis of 2 at wavelengths above 400nm gives 3 and 4, while photolysis at 254 nm gives 5. These are products are novel strained hydrocarbons. Confirmation of their structures was obtained by comparing their experimental IR spectra with that computed at B3LYP/6-311G(d,p). Table 1 compares the experimental and computed IR absorptions for 2-5. Note in particular the fine agreement between the two, especially the predicted changes due to i>d₄ substitution for all the phenyl positions.

Table 1. Experimental and Calculated vibrational frequencies (cm^-1) of 2-5.¹

The computed structures of 2-5 and their relative energies are shown in Figure 1. Triplet 1 is the lowest energy isomer, with the singlet-triplet gap of 6.22 kcal mol^-1. This compares with recent high-level computations which give a value of 13.8 kcal mol^-1. ² The other structures are much higher in energy. These other isomers have unusual bonding environments – 3 contains the strained methylenecyclopropane group, 4 is an anti-Bredt compound, and 5 is a very strained tricycle. These compounds can only be prepared by the application of light to provide the energy needed for their creation.

2 Triplet 0.0 Singlet 6.22	3 19.20
4 25.74	5 48.64

Figure 1. B3LYP/6-311G(d,p) optimized structures of 2-5 and their relative energies (kcal mol^-1).¹

References

(1) Neuhaus, P.; Grote, D.; Sander, W., "Matrix Isolation, Spectroscopic Characterization, and Photoisomerization of m-Xylylene," J. Am. Chem. Soc., 2008, 130, 2993-3000, DOI: 10.1021/ja073453d.

(2) Wang, T.; Krylov, A. I., "The effect of substituents on electronic states’ ordering in meta-xylylene diradicals: Qualitative insights from quantitative studies," J. Chem. Phys., 2005, 123, 104304, DOI: 10.1063/1.2018645.

InChIs

2: InChI=1/C8H8/c1-7-4-3-5-8(2)6-7/h3-6H

3: InChI=1/C8H8/c1-5-3-4-7-6(2)8(5)7/h3-4,7-8H,1-2H2; InChIKey=IAJQBWKVTDKBHW-UHFFFAOYAA

4: InChI=1/C8H8/c1-6-2-3-7-5-8(7)4-6/h2-4,7H,1,5H2; InChIKey=XSFFUTQMPAAWHN-UHFFFAOYAU

5: InChI=1/C8H8/c1-3-5-4(2)7-6(3)8(5)7/h5-8H,1-2H2; InChIKey=USZJYFGTTGREFL-UHFFFAOYAB