Here are two nice examples of the use of computed spectra in identifying the structure of large molecules.

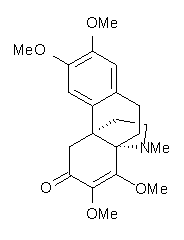
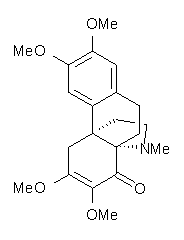
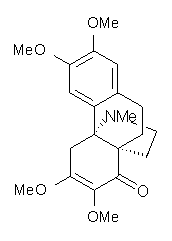
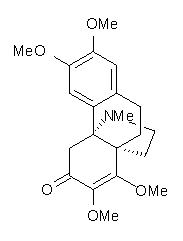
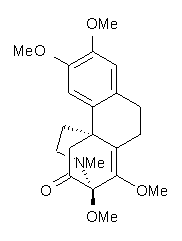
Castle and co-workers describe the synthesis of what they hoped would be runanine 1.¹ However, after they had completed their synthesis, the ¹H NMR spectrum of their product differed significantly from that of runanine. Further the optical rotation of 1 is -400, while that of their product is -34. Speculating on what might be the product they came up with 4 alternative structures 2-5. The ¹³C NMR of 1-5 were then computed by optimizing the structures at mPW1PW91/6-31G* followed by a GIAO computation at mPW1PW91/aug-cc-pVDZ with PCM (solvent is chloroform). The differences between the computed chemical shifts for 1-5 and the experimental shifts of the obtained product are summarized in Table 1. The authors conclude that their product is 5, a compound they name isorunanine.

Table 1. Average difference and maximum difference between the computed and experimental ¹³ C chemical shifts (ppm).

The authors also report the rather poor agreement between the computer spectrum of 6 and the experimental spectrum in benzene. Unfortunately, not enough details are provided to really determine where errors might be occurring. For example, there is no indication of examining multiple conformations (and those methoxy groups can rotate along with the inversion at the amine). Once again, the supporting materials, while extensive in terms of experimental NMR spectra, contain no details of the computed structures.

The structure of hypurticin 6 was determined using a comparison of computed coupling constants.² Here the authors first assumed that four possible stereoisomers are possible 6a-d, given that the other stereocenters were determined unambiguously by experiment and biogenesis considerations. B3LYP/6-31G(d) optimization of a restricted set of conformations led to the lowest energy conformer. The coupling constants computed for these four structures indicated the closet agreement between the computed constants of 6a with experimental values. An exhaustive search of the conformational space of each of these diastereomers at B3LYP/DGDZVP followed by Boltzmann weighting of the coupling constants confirmed that 6a is the structure of hypurticin.

References

(1) Nielsen, D. K.; Nielsen, L. L.; Jones, S. B.; Toll, L.; Asplund, M. C.; Castle, S. L., "Synthesis of Isohasubanan Alkaloids via Enantioselective Ketone Allylation and Discovery of an Unexpected Rearrangement," J. Org. Chem. 2009, 74, 1187-1199, DOI: 10.1021/jo802370v.

(2) Mendoza-Espinoza, J. A.; Lopez-Vallejo, F.; Fragoso-Serrano, M.; Pereda-Miranda, R.; Cerda-Garcia-Rojas, C. M., "Structural Reassignment, Absolute Configuration, and Conformation of Hypurticin, a Highly Flexible Polyacyloxy-6-heptenyl-5,6-dihydro-2H-pyran-2-one," J. Nat. Prod. 2009, 72, 700-708, DOI: 10.1021/np800447k.

Torquoselectivity rules (discussed in Chapter 3.5 of my book) indicate that 3-phenylcyclobutene will ring-open to give the outward rotated product (Reaction 1). Houk and Tang report a seeming contradiction, namely the ring opening of 1 gives only the inward product 3 (Reaction 2).¹

B3LYP/6-31G* computations on the ring-opening of 4 indicate that the activation barrier for the outward path (leading to 5) is nearly 8 kcal mol^-1 lower than the barrier for the inward path (leading to 6, see Reaction 3). This is consistent with torquoselectivity rules, but what is going on in the experiment?

In the investigation of the isomerization of the outward to inward pathway, they discovered a low-energy pyran intermediate 7. This led to the proposal of the mechanism shown in Reaction 3. The highest barrier is for the electrocyclization that leads to the outward product 5. The subsequent barriers – the closing to the pyran 7 and then the torquoselective ring opening to 6 –  are about than 13 kcal mol^-1 lower in energy than for the first step. The observed product is the thermodynamic sink. And the nice thing about this mechanism is that torquoselection is preserved.

References

(1) Um, J. M.; Xu, H.; Houk, K. N.; Tang, W., "Thermodynamic Control of the Electrocyclic
Ring Opening of Cyclobutenes: C=X Substituents at C-3 Mask the Kinetic Torquoselectivity," J. Am. Chem. Soc. 2009, 131, 6664-6665, DOI: 10.1021/ja9016446.

InChIs

4: InChI=1/C16H16O6/c1-20-13(17)11-9-16(14(18)21-2,15(19)22-3)12(11)10-7-5-4-6-8-10/h4-9,12H,1-3H3
InChIKey=VBOGEHVOAGDMNG-UHFFFAOYAR

5: InChI=1/C16H16O6/c1-20-14(17)12(9-11-7-5-4-6-8-11)10-13(15(18)21-2)16(19)22-3/h4-10H,1-3H3/b12-9-
InChIKey=PZRWKBUUAFMPBC-XFXZXTDPBF

6: InChI=1/C16H16O6/c1-20-14(17)12(9-11-7-5-4-6-8-11)10-13(15(18)21-2)16(19)22-3/h4-10H,1-3H3/b12-9+
InChIKey=PZRWKBUUAFMPBC-FMIVXFBMBS

7: InChI=1/C16H16O6/c1-19-14(17)11-9-12(15(18)20-2)16(21-3)22-13(11)10-7-5-4-6-8-10/h4-9,13H,1-3H3/t13-/m0/s1
InChIKey=QSJZITDSTPMCEM-ZDUSSCGKBG

Back when I was first learning ab initio methods in Cliff Dykstra’s lab, I played a bit with the post-HF method CEPA (couple electron pair approximation). This method fell out of favor over the years with the rise of MP theory and then with DFT. Now, Neese and Grimme and co-workers are resurrecting it.¹ Their Accounts article provides a series of tests of CEPA/1 against benchmark computations (typically CCSD(T)) and lo and behold, CEPA performs remarkably well! It bests B3LYP (no surprise there), B2LYP and MP2 in virtually every category, ranging from reaction energies, hydrogen bond energies, van der Waals interaction energies, and activation barrier heights. As an example, for the isomerization energy of toluene to norbornadiene, CCSD(T) estimates the energy is 42.79 kcal mol^-1. B3LYP does miserably, with an error of nearly 14 kcal mol^-1, but the CEPA/1 estimate is off by only 0.04 kcal mol^-1. Since the computational time of CEPA/1 is competitive with MP2, the authors conclude that CEPA/1 is well-worth reinvestigating as an alternative post-HF methodology.

References

(1) Neese, F.; Hansen, A.; Wennmohs, F.; Grimme, S., "Accurate Theoretical Chemistry with Coupled Pair Models," Acc. Chem. Res. 2009, 42, 641-648 DOI: 10.1021/ar800241t.

Computed NMR spectra have been a major theme of the blog (see these posts). General consensus is that they can be enormously helpful in characterizing structures and stereochemistry, but there has been a nagging sense that one needs to use very large basis sets to get reasonable accuracies.

Bally and Rablen¹ now confront that claim and suggest instead that quite modest basis sets along with a number of flavors of DFT can provide very good ¹H NMR shifts. They examined 80 organic molecules spanning a variety of functional groups. A key feature is that these molecules exist as a single conformation or their conformational distribution is dominated by one conformer. This avoids the need of computing a large number of conformers and taking a Boltzman average of their shifts – a task that would likely require a much larger basis set than what they hope to get away with.

The most important conclusion: the WP04 functional,² developed by Cramer to predict proton spectra, with the very small 6-31G(d,p) basis set and incorporation of the solvent through PCM provides excellent cost/benefit performance. The rms error of the proton chemical shifts is 0.198 ppm, and this can be reduced to 0.140 ppm with scaling. The 6-31G(d) basis set is even better if one uses a linear scaling; its error is only 0.120 ppm. B3LYP/6-31G(d,p) has an rms only somewhat worse. Use of aug-cc-pVTZ basis sets, while substantially more time consuming, provides inferior predictions.

The authors contend that this sort of simple DFT computation, affordable for many organic systems on standard desktop PCs, should be routinely done, especially in preference to increment schemes that are components of some drawing programs. And if a synthesis group does not have the tools to do this sort of work, I’m sure there are many computational chemists that would be happy to collaborate!

References

(1) Jain, R.; Bally, T.; Rablen, P. R., "Calculating Accurate Proton Chemical Shifts of Organic Molecules with Density Functional Methods and Modest Basis Sets," J. Org. Chem. 2009, DOI: 10.1021/jo900482q.

(2) Wiitala, K. W.; Hoye, T. R.; Cramer, C. J., "Hybrid Density Functional Methods Empirically Optimized for the Computation of ¹³C and ¹H Chemical Shifts in Chloroform Solution," J. Chem. Theory Comput. 2006, 2, 1085-1092, DOI: 10.1021/ct6001016

A computational study of addition of singlet carbenes to bicyclobutanes reveals another potential energy surface where dynamics may be active. Rablen, Jones and co-workers examined the reaction of dichlorocarbene with bicyclobutane 1 and 1,2,2-trimethylbicyclobutane 2 (Reactions 1 and 2) using a number of computational techniques.¹

For reaction 1, they identified three reaction pathways. The first two involve the carbene approaching along the central C-C bond. Path A (Scheme 1) involves a single transition state that leads to product 3, with a barrier of 8.4 kcal mol^-1. The second pat (pathway B), leads to critical point 4, which is a transition state at HF/6-31G* and QCISD/6-31G* but is a local minimum at CCSD/6-31G*. This minimum however is very shallow, and vibrational energy will exceed the barriers about it. Both pathways indicate an asynchronous but concerted reaction. The last pathway (C) is for insertion of the carbine into the bridgehead C-C bond, leading to the bicyclo product 5. This barrier is very high, 27 kcal mol^-1, and so this path is unlikely to be competitive.

Experimental study of Reaction 2 showed that only 6 is produced.² Rablen and Jones identified six pathways where the carbene attacks 2 along the bridgehead bond (analogous to Paths A and B, except there are three rotamers and the attack can be at either bridgehead carbon) and the insertion path that leads to 8. Once again, this last pathway has a very large barrier and is non-competitive. Attack at the unsubstituted bridgehead carbons is favored over attack at the methyl-substituted bridgehead by 2-3 kcal mol^-1. The path that leads directly to 7 has a slightly lower barrier (0.4 kcal mol^-1) than the path that leads directly to 8. The analog of Path B leads here to a true intermediate 9 through a barrier 0.4 kcal mol^-1 higher than the barrier that leads to 7. This intermediate is shown in Figure 1.

Figure 1. CCSD/6-31G* structure of intermediate 9.¹

The energies of the barriers suggest that 7 will be the major product, but not the exclusive product. Rablen and Jones point out that intermediate 9 lies in a very shallow plateau and exit from this intermediate can lead to either 7 or 8. This sort of potential energy surface has been implicated in reactions that exhibit non-statistical behavior indicative of dynamic effects (see Chapter 7 of my book). Rablen and Jones speculate that dynamics might be dictating the product distribution in Reaction 2 as well. Confirmation awaits a molecular dynamics study.

References

(1) Rablen, P. R.; Paiz, A. A.; Thuronyi, B. W.; Jones, M., "Computational Investigation of the Mechanism of Addition of Singlet Carbenes to Bicyclobutanes," J. Org. Chem. 2009, DOI: 10.1021/jo900485z

(2) Jackson, J. E.; Mock, G. B.; Tetef, M. L.; Zheng, G.-x.; Jones, M., "Reactions of carbenes with bicyclobutanes and quadricyclane : Cycloadditions with two σ bonds," Tetrahedron 1985, 41, 1453-1464, DOI: 10.1016/S0040-4020(01)96386-0.

InChIs

1: InChI=1/C4H6/c1-3-2-4(1)3/h3-4H,1-2H2
InChIKey=LASLVGACQUUOEB-UHFFFAOYAV

2: InChI=1/C7H12/c1-6(2)5-4-7(5,6)3/h5H,4H2,1-3H3
InChIKey=GJMVYBBYZUWWLJ-UHFFFAOYAI

3: InChI=1/C5H6Cl2/c1-2-3-4-5(6)7/h2,4H,1,3H2
InChIKey=FGUOQAVVVDPABB-UHFFFAOYAR

5: InChI=1/C5H6Cl2/c6-5(7)3-1-4(5)2-3/h3-4H,1-2H2
InChIKey=SUZACPSWEYRCBD-UHFFFAOYAW

6: InChI=1/C8H12Cl2/c1-6(2)8(3,4)5-7(9)10/h5H,1H2,2-4H3
InChIKey=QIFFCMZJZYIIBA-UHFFFAOYAZ

7: InChI=1/C8H12Cl2/c1-6(2)7(3)4-5-8(9)10/h5H,4H2,1-3H3
InChIKey=MOELQSRRCNAPQV-UHFFFAOYAX

8: InChI=1/C8H12Cl2/c1-6(2)5-4-7(6,3)8(5,9)10/h5H,4H2,1-3H3
InChIKey=PRCOWYZGJRWGOB-UHFFFAOYAP

Can one steer the course of a reaction by selectively applying a force to a molecule? Atomic force microscopy opens up this avenue. Martinez¹ has just published a computational study on the ring opening of cyclobutene with applied forces. Cyclobutene should ring-open in a conrotatory fashion according to the Woodward-Hoffman rules. But Martinez shows that by pulling on cyclobutene in a cis fashion, the disrotatory pathway can become the more favored route. Thus, it appears that mechanochemistry might be an alternative way to create selectivity in chemical reactions!

References

(1) Ong, M. T.; Leiding, J.; Tao, H.; Virshup, A. M.; Martinez, T. J., “First Principles Dynamics and Minimum Energy Pathways for Mechanochemical Ring Opening of Cyclobutene,” J. Am. Chem. Soc., 2009, 131, 6377-6379, DOI: 10.1021/ja8095834.

InChIs

cyclobutene: InChI=1/C4H6/c1-2-4-3-1/h1-2H,3-4H2
InChIKey: CFBGXYDUODCMNS-UHFFFAOYAN

Houk¹ examined the Mannich reaction of the enamine formed from acetone and S-proline with N-ethylidine-N-phenylamine (see Chapter 5.3.3 in my book). Parasuk and Parasuk now extend this to the reaction of the enamine of cyclohexanone and S-proline with N-phenylmethanimine (Reaction 1).² Geometries were optimized at B3LYP/6-31++G(d,p) and single-point energies computed with PCM (for the solvent DMSO) at both B3LYP and MP2.

Reaction 1

First, they examined the formation of the enamine 1, which can be in the syn or anti conformation. The barrier for formation of the syn isomer is 10.2 kcal mol^-1. The barrier for the formation of the anti conformer is much higher, 17.9 kcal mol^-1, and this is with a single water molecule used to assist the proton migration. However, the rotational barrier between the two conformers is only 4.2 kcal mol^-1. So, they conclude that the syn isomer is the only conformer directly formed by the reaction of cyclohexanone and S-proline, and then rotation can produce the anti conformer.

The located the transition state for the reaction of either syn–1 or anti–1 with phenylmethanimine. The two transition states are shown in Figure 1. The barrier for the reaction of syn–1 is 8.5 kcal mol^-1, leading to the S product. The other barrier is higher, 13.0 kcal mol^-1, and the R product 2R is 6.8 kcal mol^-1 higher in energy than the S product 2S. Thus, the reaction to give the S product is both kinetically and thermodynamically favored. This is consistent with experiment³ which gives the S product with 99%ee. Inclusion of solvent makes the S product even more thermodynamically and kinetically favored over the R isomer.

TS-2S

TS-2R

Figure 1. B3LYP/6-311++G(d,p) optimized transition states leading to 2S and 2R.²

References

(1) Bahmanyar, S.; Houk, K. N., "Origins of Opposite Absolute Stereoselectivities in Proline-Catalyzed Direct Mannich and Aldol Reactions," Org. Lett. 2003, 5, 1249-1251, DOI: 10.1021/ol034198e.

(2) Parasuk, W.; Parasuk, V., "Theoretical Investigations on the Stereoselectivity of the Proline Catalyzed Mannich Reaction in DMSO," J. Org. Chem. 2008, 73, 9388-9392, DOI: 10.1021/jo801872w.

(3) Ibrahem, I.; Zou, W.; Casas, J.; Sundén, H.; Córdova, A., "Direct organocatalytic enantioselective α-aminomethylation of ketones," Tetrahedron 2006, 62, 357-364, DOI: 10.1016/j.tet.2005.08.113.

InChIs

1: InChI=1/C11H17NO2/c13-11(14)10-7-4-8-12(10)9-5-2-1-3-6-9/h5,10H,1-4,6-8H2,(H,13,14)/t10-/m0/s1/f/h13
InChIKey=FGOQJKISPWOYSX-WSLRCUSADU

2S: InChI=1/C18H24N2O2/c21-18(22)16-10-6-11-17(16)20-12-5-4-9-15(20)13-19-14-7-2-1-3-8-14/h1-3,7-8,15-16,19H,4-6,9-13H2/b20-17+/t15-,16+/m0/s1
InChIKey=SDMHQUCIHUXJMJ-OQSOEKIEBW

2R: InChI=1/C18H24N2O2/c21-18(22)16-10-6-11-17(16)20-12-5-4-9-15(20)13-19-14-7-2-1-3-8-14/h1-3,7-8,15-16,19H,4-6,9-13H2/b20-17-/t15-,16-/m1/s1
InChIKey=SDMHQUCIHUXJMJ-HGWRPWPUBS