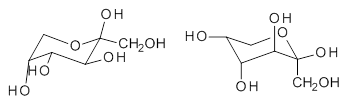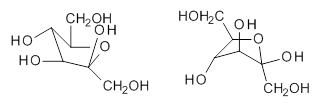Comparing S_N2 and S_N1 reactions using computational methods is often quite difficult. The problem is that the heterolytic cleavage in the S_N1 reaction leads to an ion pair, and in the gas phase this is a highly endothermic process. Optimization of the ion pair in the gas phase invariably leads to recombination. This is disturbingly the result even when one uses PCM to mimic the solvent, which one might have hoped would be sufficient to stabilize the ions.

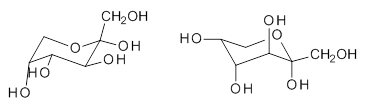
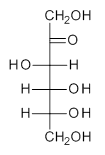
The computational study of the glycoside cleavage by Hosoya and colleagues offers some guidance towards dealing with this problem.¹ They examined the cleavage of triflate from 2,3,4,6-tetra-O-methyl-α-D-glucopyranosyl triflate 1.

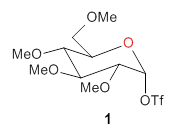
Benchmarking the dissociation energy for the cleavage of 1 and considering computational performance, they settled on M06-2X/BS-III//M06-2X/BS-I, where BS-III is aug-cc-pVTZ basis set for O, F, and Cl and cc-pVTZ for H, C, and S and BS-I is 6-31G(d,p) basis sets were employed for H, C, and S, and 6-31+G(d) for O, F, and Cl. Solvent (dichloromethane) was included through PCM.

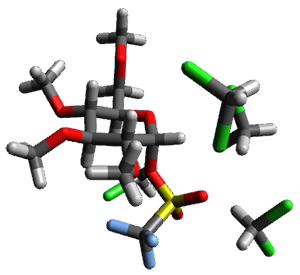
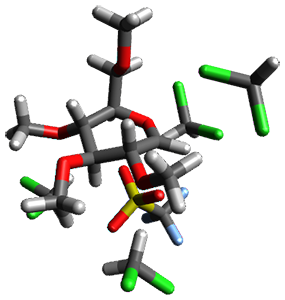
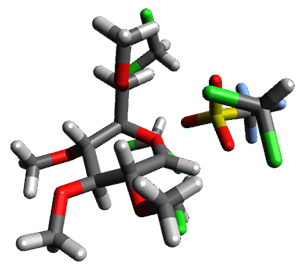
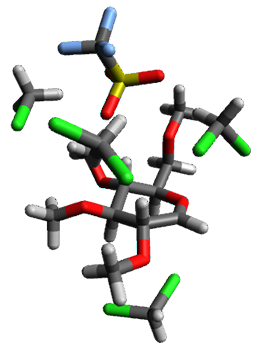
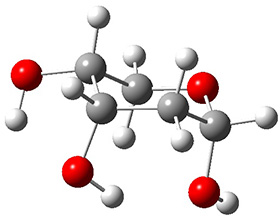
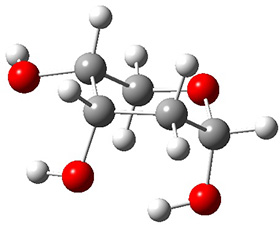
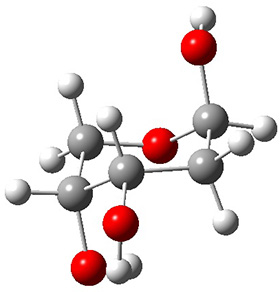
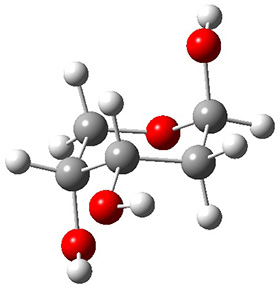
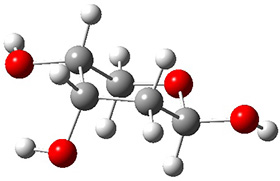
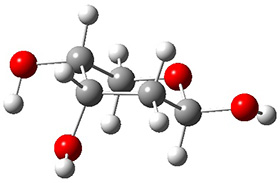
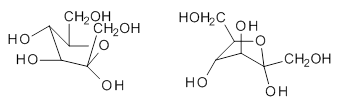
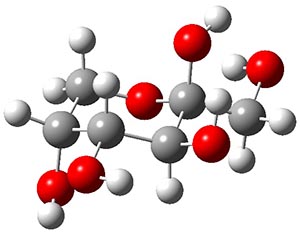
Attempted optimization of the contact ion pair formed from cleavage of 1 invariably led back to the covalent bound 1. PCM is not capable of properly stabilizing these types of ions in proximity. To solve this problem, they incorporated four explicit dichloromethane molecules. A minor drawback to their approach is that they did not sample much of configuration space and so their best geometries may not be the lowest energy configurations. Nonetheless, with four solvent molecules, they were able to locate contact ion pairs and solvent-separated ion pairs. Representative examples are shown in Figure 1. This method of explicit incorporation of a few solvent molecules seems to be the direction we must take to treat ions or even highly polar molecules in solution.

1 0.0	1-CIP 8.5
1-SSIPa 8.4	1-SSIPb 11.1

Figure 1. Representative examples of microsolvated 1, its contact ion pair (CIP) and solvent separated ion pair (SSIP) computed at M06-2X/BS-III//M06-2X/BS-I, and relative energies (kcal mol^-1)

References

(1) Hosoya, T.; Takano, T.; Kosma, P.; Rosenau, T. "Theoretical Foundation for the Presence of Oxacarbenium Ions in Chemical Glycoside Synthesis," J. Org. Chem. 2014, 79, 7889-7894, DOI: 10.1021/jo501012s.

InChIs

1: InChI=1S/C11H19F3O8S/c1-17-5-6-7(18-2)8(19-3)9(20-4)10(21-6)22-23(15,16)11(12,13)14/h6-10H,5H2,1-4H3/t6-,7-,8+,9-,10-/m1/s1
InChIKey=RPZNYYCDDYUPJR-HOTMZDKISA-N

The conformational space of monosaccharides is amazingly complex. If we consider just the pyranose form, the ring can in principal exist as a chair, a half-chair, skew (or twist boat) and boat form, for a total of 38 puckering configurations. Layer on top of this the axial and equatorial positions of the hydroxyl and methylhydroxyl groups, and then the rotamers of these substituents, and one is faced with a dauntingly vast space. It is just this space that Beckham and co-workers¹ take on for α- and β-glucose, β-xylose, β-mannose and β-acetylglucosamine.

For each sugar, and for each of the 38 puckering configurations, full rotamer scans for each of the substituents led to 27,702 conformations of each of the four monosaccharides, and 36,936 conformations of β-acetylglucosamine. This totals to over 123,000 geometry optimizations that were carried out at M06-2x/6-31G(d). Then taking the structures within 5 kcal mol^-1 of the lowest energy structure for ­each pucker, they reoptimized at M06-2X/6-31+G(d,p). Pruning once again those structures that were above 5 kcal mol^-1 of the minimum, they performed CCSD(T)/6-311+G(d,p)//B3LYP/6-311+G(2df,p) computations. What a tour de force!

The results of these conformational space surveys are not terribly exciting. The substituents do make a difference in dictating the most and least favorable structures and the activation barriers for interconversion of ring forms.

These PESs will be quite useful in understanding carbohydrate conformations and the role these may play in their chemistry. But the point of bringing this paper to your attention is the tremendously complex, detailed PES that is uncovered, representing the scale of what can be done with modern computers and modern algorithms.

References

(1) Mayes, H. B.; Broadbelt, L. J.; Beckham, G. T. "How Sugars Pucker: Electronic Structure Calculations Map the Kinetic Landscape of Five Biologically Paramount Monosaccharides and Their Implications for Enzymatic Catalysis," Journal of the American Chemical Society 2013, 136, 1008-1022, DOI: 10.1021/ja410264d.

InChIs

α-glucose: InChI=1S/C6H12O6/c7-1-2-3(8)4(9)5(10)6(11)12-2/h2-11H,1H2/t2-,3-,4+,5-,6+/m1/s1
InChIKey: WQZGKKKJIJFFOK-DVKNGEFBSA-N

β-glucose: InChI=1S/C6H12O6/c7-1-2-3(8)4(9)5(10)6(11)12-2/h2-11H,1H2/t2-,3-,4+,5-,6-/m1/s1
InChIKey=WQZGKKKJIJFFOK-VFUOTHLCSA-N

β-xylose: InChI=1S/C5H10O5/c6-2-1-10-5(9)4(8)3(2)7/h2-9H,1H2/t2-,3+,4-,5-/m1/s1
InChIKey=SRBFZHDQGSBBOR-KKQCNMDGSA-N

β-mannose: InChI=1S/C6H12O6/c7-1-2-3(8)4(9)5(10)6(11)12-2/h2-11H,1H2/t2-,3-,4+,5+,6-/m1/s1
InChIKey=WQZGKKKJIJFFOK-RWOPYEJCSA-N

β-acetylglucosamine: InChI=1S/C8H15NO6/c1-3(11)9-5-7(13)6(12)4(2-10)15-8(5)14/h4-8,10,12-14H,2H2,1H3,(H,9,11)/t4-,5-,6-,7-,8-/m1/s1
InChIKey=OVRNDRQMDRJTHS-FMDGEEDCSA-N

2-deoxyribose 1 is undoubtedly one of the most important sugars as it is incorporated into the backbone of DNA. The conformational landscape of 1 is complicated: it can exist as an open chain, as a five-member ring (furanose), or a six-member ring (pyranose), and intramolecular hydrogen bonding can occur. This internal hydrogen bonding is in competition with hydrogen bonding to water in aqueous solution. Unraveling all this is of great interest in predicting structures of this and a whole host of sugar and sugar containing-molecules.

1

In order to get a firm starting point, the gas phase structures of the low energy conformers of 1 would constitute a great set of structures to use as a benchmark for gauging force fields and computational methods. Cocinero and Alonso¹ have performed a laser ablation molecular beam Fourier transform microwave (LA-MB-FTMW) experiment (see these posts for other studies using this technique) on 1 and identified the experimental conformations by comparison to structures obtained at MP2/6-311++G(d,p). Unfortunately the authors do not include these structures in their supporting materials, so I have optimized the low energy conformers of 1 at ωB97X-D/6-31G(d) and they are shown in Figure 1.

1a (0.0)	1b (4.7)
1c (3.3)	1d (5.6)
1e (8.9)	1f (9.4)

Figure 1. ωB97X-D/6-31G(d) optimized structures of the six lowest energy conformers of 1. Relative free energy in kJ mol^-1.

The computed spectroscopic parameters were used to identify the structures responsible for the six different ribose conformers observed in the microwave experiment. To give a sense of the agreement between the computed and experimental parameters, I show these values for the two lowest energy conformers in Table 1.

Table 1. MP2/6-311++G(d,p) computed and observed spectroscopic parameters for the two lowest energy conformers of 1.

This is yet another excellent example of the symbiotic relationship between experiment and computation in structure identification.

References

(1) Peña, I.; Cocinero, E. J.; Cabezas, C.; Lesarri, A.; Mata, S.; Écija, P.; Daly, A. M.; Cimas, Á.; Bermúdez, C.; Basterretxea, F. J.; Blanco, S.; Fernández, J. A.; López, J. C.; Castaño, F.; Alonso, J. L. "Six Pyranoside Forms of Free 2-Deoxy-D-ribose," Angew. Chem. Int. Ed. 2013, 52, 11840-11845, DOI: 10.1002/anie.201305589.

InChIs

1a: InChI=1S/C5H10O4/c6-3-1-5(8)9-2-4(3)7/h3-8H,1-2H2/t3-,4+,5-/m0/s1
InChIKey=ZVQAVWAHRUNNPG-LMVFSUKVSA-N

Sugars comprise a very important class of organic compounds for a variety of reasons, including dietary needs. On the chemical side, their stereochemical variations give rise to interesting
conformational questions. While sugar structures are a well-studied dating back to Fischer, most of these studies are in the solid or solution phase, and these phases can certainly play a role in dictating conformational preferences. This is seen in the differences in conformational distribution with different solvents. Only recently has instrumentation been developed (see these posts for some earlier applications: A, B, C) that can provide structural information of sugars in the gas phase. Cocinero and co-workers describe just such an analysis of fructose.¹

Using a combination of laser ablation Fourier transform microwave spectroscopy and quantum chemical computations, they have examined the gas-phase structure of this ketose. There are
quite a number of important conformational and configurational isomers to consider, as shown in Scheme 1. Fructose can exist in a pyranose form (6-member ring) with the anomeric carbon being α or β. An alternative cyclic form is the 5-member ring furanose form, which again has the two options at the anomeric position. Both the 5- and 6-member rings can ring flip, giving rise to 4 pyranose and 4 furanose forms. Of course there is also the
acyclic form.

Scheme 1. Major Frucotse isomers

The observed microwave spectrum is quite simple, showing evidence of only a single isomer. In comparing the microwave rotational constants and the quartic centrifugal distortion constants with those obtained from MP2 and M06-2x computations, it is clear that the only observed isomer is the β-pyranose isomer in its ²C₅ conformation.

Both MP2 and M06-2x (with a variety of TZ basis sets) predict this isomer to be the lowest energy form by about 2.5 kcal mol^-1. This structure is shown in Figure 1. Interestingly, B3LYP predicts the open chain configuration as the most stable isomer, with the β-pyranose isomer about 0.5 kcal mol^-1 higher in energy. The authors strongly caution against using B3LYP for any sugars.

Figure 1. MP2/maug-cc-pVTZ optimized structure of β-fructopyranose.

This most stable furanose isomer displays five intramolecular hydrogen bonds that account for its stability over all other possibilities. However, the pyranose form of fructose is very rare in nature, and the Protein Data Bank has only four examples. The furanose form is by far the more commonly found isomer (as in sucrose). Clearly, hydrogen bonding to solvent and other solvent interactions alter the conformational distribution.

References

(1) Cocinero, E. J.; Lesarri, A.; Ecija, P.; Cimas, A.; Davis, B. G.; Basterretxea, F. J.; Fernandez, J. A.; Castano, F. "Free Fructose is Conformationally Locked," J. Am. Chem. Soc. 2013, 135, 2845-2852, DOI: 10.1021/ja312393m.

InChIs:

β-fructopyranose:
InChI=1S/C5H10O6/c6-2-1-11-5(9,10)4(8)3(2)7/h2-4,6-10H,1H2
InChIKey=FFDHYUUPNCCTDA-UHFFFAOYSA-N

A comprehensive evaluation of how different computational methods perform in predicting the energies of monosaccharides comes to some very interesting conclusions. Sameera and Pantazis¹ have examined the eight different aldohexoses (allose, alltrose, glucose, mannose, gulose, idose, galactose and talose), specifically looking at different rotomers of the hydroxymethyl group, α- vs. β-anomers, pyranose vs. furanose isomers, ring conformations (¹C₄ vs skew boat forms), and ring vs. open chain isomers. In total, 58 different structures were examined. The benchmark computations are CCSD(T)/CBS single point energies using the SCS-MP2/def2-TZVPP optimized geometries. The RMS deviation from these benchmark energies for some of the many different methods examined are listed in Table 1.

Table 1. Average RMS errors (kJ mol^-1) of the 58 different monosaccharide structures for
different computational methods.

Perhaps the most interesting take-home message is that CEPA, MP2, the double hybrid methods and M06-2x all do a very good job at evaluating the energies of the carbohydrates. Given the significant computational advantage of M06-2x over these other methods, this seems to be the functional of choice! The poorer performance of the DFT methods over the ab initio methods is primarily in the relative energies of the open-chain isomers, where errors can be on the order of 10-20 kJ mol^-1 with most of the functionals; even the best overall methods (M06-2x and the double hybrids) have errors in the relative energies of the open-chain isomers of 7 kJ mol^-1. This might be an area of further functional development to probe better treatment of the open-chain aldehydes vs. the ring hemiacetals.

References

(1) Sameera, W. M. C.; Pantazis, D. A. "A Hierarchy of Methods for the Energetically Accurate Modeling of Isomerism in Monosaccharides," J. Chem. Theory Comput. 2012, 8, 2630-2645, DOI:10.1021/ct3002305