What is the size of a molecule that will stretch computational resources today? Chan and co-workers have examined some very large fullerenes1 to both answer that question, and also to explore how large a fullerene must be to approach graphene-like properties.
They are interested in predicting the heat of formation of large fullerenes. So, they benchmark the heats of formation of C60 using four different isodesmic reactions (Reaction 1-4), comparing the energies obtained using a variety of different methods and basis sets to those obtained at W1h. The methods include traditional functionals like B3LYP, B3PW91, CAM-B3LYP, PBE1PBE, TPSSh, B98, ωB97X, M06-2X3, and MN12-SX, and supplement them with the D3 dispersion correction. Additionally a number of doubly hybrid methods are tested (again with and without dispersion corrections), such as B2-PLYP, B2GPPLYP, B2K-PLYP, PWP-B95, DSD-PBEPBE, and DSD-B-P86. The cc-pVTZ and cc-pVQZ basis sets were used. Geometries were optimized at B3LYP/6-31G(2df,p).
|
C60 + 10 benzene → 6 corannulene |
Reaction 1 |
|
C60 + 10 naphthalene → 8 corannulene |
Reaction 2 |
|
C60 + 10 phenanthrene → 10 corannulene |
Reaction 3 |
|
C60 + 10 triphenylene → 12 corannulene |
Reaction 4 |
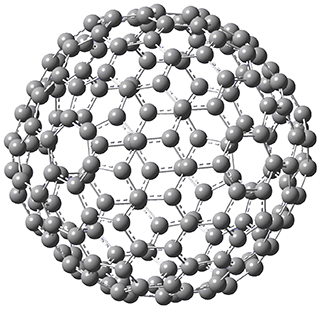
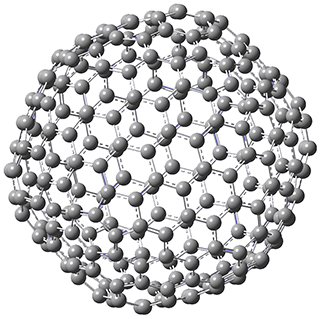
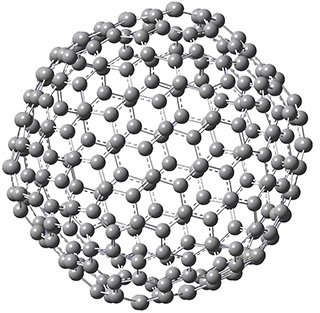
Excellent results were obtained with DSD-PBEPBE-D3/cc-pVQZ (an error of only 1.8 kJ/mol), though even a method like BMK-D3/cc-pVTZ had an error of only 9.2 kJ/mol. They next set out to examine large fullerenes, including such behemoths as C180, C240, and C320, whose geometries are shown in Figure 1. Heats of formation were obtained using isodesmic reactions that compare back to smaller fullerenes, such as in Reaction 5-8.
|
C70 + 5 styrene → C60 + 5 naphthalene |
Reaction 5 |
|
C180 → 3 C60 |
Reaction 6 |
|
C320 + 2/3 C60 → 2 C180 |
Reaction 7 |
|
C180 |
|
C240 |
|
C320 |
Figure 1. B3LYP/6-31G(2df,p) optimized geometries of C180, C240, and C320. (Don’t forget that clicking on these images will launch Jmol and allow you to manipulate the molecules in real-time.)
Next, taking the heat of formation per C for these fullerenes, using a power law relationship, they were able to extrapolate out the heat of formation per C for truly huge fullerenes, and find the truly massive fullerenes, like C9680, still have heats of formation per carbon 1 kJ/mol greater than for graphene itself.
References
(1) Chan, B.; Kawashima, Y.; Katouda, M.; Nakajima, T.; Hirao, K. "From C60 to Infinity: Large-Scale Quantum Chemistry Calculations of the Heats of Formation of Higher Fullerenes," J. Am. Chem. Soc. 2016, 138, 1420-1429, DOI: 10.1021/jacs.5b12518.