2-deoxyribose 1 is undoubtedly one of the most important sugars as it is incorporated into the backbone of DNA. The conformational landscape of 1 is complicated: it can exist as an open chain, as a five-member ring (furanose), or a six-member ring (pyranose), and intramolecular hydrogen bonding can occur. This internal hydrogen bonding is in competition with hydrogen bonding to water in aqueous solution. Unraveling all this is of great interest in predicting structures of this and a whole host of sugar and sugar containing-molecules.
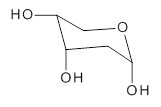
1
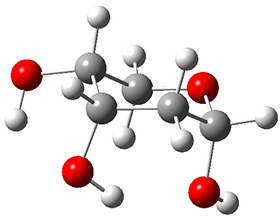
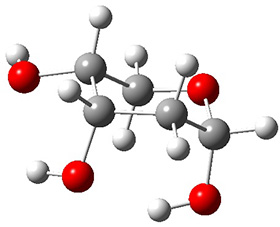
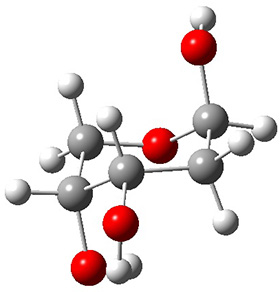
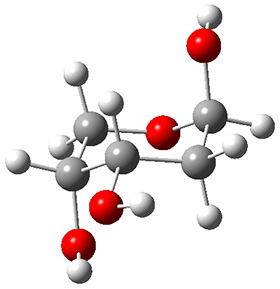
In order to get a firm starting point, the gas phase structures of the low energy conformers of 1 would constitute a great set of structures to use as a benchmark for gauging force fields and computational methods. Cocinero and Alonso1 have performed a laser ablation molecular beam Fourier transform microwave (LA-MB-FTMW) experiment (see these posts for other studies using this technique) on 1 and identified the experimental conformations by comparison to structures obtained at MP2/6-311++G(d,p). Unfortunately the authors do not include these structures in their supporting materials, so I have optimized the low energy conformers of 1 at ωB97X-D/6-31G(d) and they are shown in Figure 1.
|
1a (0.0) |
1b (4.7) |
|
1c (3.3) |
1d (5.6) |
|
1e (8.9) |
1f (9.4) |
Figure 1. ωB97X-D/6-31G(d) optimized structures of the six lowest energy conformers of 1. Relative free energy in kJ mol-1.
The computed spectroscopic parameters were used to identify the structures responsible for the six different ribose conformers observed in the microwave experiment. To give a sense of the agreement between the computed and experimental parameters, I show these values for the two lowest energy conformers in Table 1.
Table 1. MP2/6-311++G(d,p) computed and observed spectroscopic parameters for the two lowest energy conformers of 1.
|
|
1a |
1c |
||
|
|
Expt |
Calc |
Expt |
Calc |
|
A(MHz) |
2484.4138 |
2492 |
2437.8239 |
2447 |
|
B (MHz) |
1517.7653 |
1533 |
1510.7283 |
1527 |
|
C (MHz) |
1238.9958 |
1250 |
1144.9804 |
1158 |
|
ΔG (kJ mol-1) |
|
0.0 |
|
3.3 |
This is yet another excellent example of the symbiotic relationship between experiment and computation in structure identification.
References
(1) Peña, I.; Cocinero, E. J.; Cabezas, C.; Lesarri, A.; Mata, S.; Écija, P.; Daly, A. M.; Cimas, Á.; Bermúdez, C.; Basterretxea, F. J.; Blanco, S.; Fernández, J. A.; López, J. C.; Castaño, F.; Alonso, J. L. "Six Pyranoside Forms of Free 2-Deoxy-D-ribose," Angew. Chem. Int. Ed. 2013, 52, 11840-11845, DOI: 10.1002/anie.201305589.
InChIs
1a: InChI=1S/C5H10O4/c6-3-1-5(8)9-2-4(3)7/h3-8H,1-2H2/t3-,4+,5-/m0/s1
InChIKey=ZVQAVWAHRUNNPG-LMVFSUKVSA-N