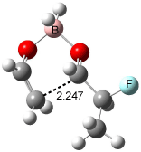Addition of enolboranes to α-substituted aldehydes
In Chapter 5.2, we discussed a number of computation studies of the origins of asymmetry in 1,2-additions. We discussed the importance of the Felkin-Anh model, but that modifications of this model are needed to rationalize the broad range of addition reactions.
One modification was presented by Frenking,1 who noted that in the addition of LiH to propanal, it was the conformation of the aldehyde that dictated the energy of the possible transition states. The lowest energy transition state is 1a, lying 1.3 kcal mol-1 below 1b and 1.6 kcal mol-1 below 1c (computed at MP2/6-31G(d)//HF/6-31G(d)). When the LiH fragment is removed and all other atoms kept frozen in their positions in the three transition states, 1a remains the lowest in energy.

A recent article by Cramer and Evans2 examined the addition of enolboranes to aldehydes and also noted the importance of the aldehyde conformation in dictating the stereochemical outcome. The main thrust was, however, that the Cram-Conforth type model for 1,2-addition is more appropriate for some enolborane additions.
This work derives from Evans’ earlier experimental study of the addition of the boron enolate of 2-methyl-3-pentanone to a-alkoxyaldehydes (Scheme 1).3 Evans suggested that there were four transition state models that give a 3,4-anti relationship in the product (Scheme 2). The Felkin-Anh model favors B, since it avoids the syn interaction, and so E enolates will have a greater anti selectivity than Z enolates. On the other hand, the Conforth model favors transition state C, and predicts that Z enolates will have greater anti selectivity. The addition of Z enolates in fact gives large anti selectivity, while addition of E enolates gives poor anti selectivity. These results are consistent with the Cram-Cornforth model.
Scheme 1.

Scheme 2.

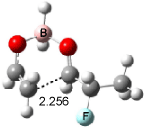
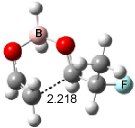
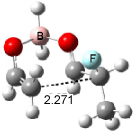
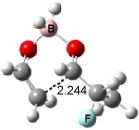
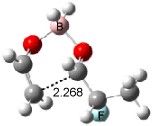
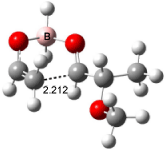
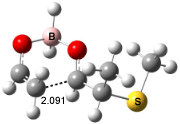
Cee, Cramer and Evans2 examined the addition of enolborane to a number of a-substituted propanal compounds. They located six transition states (Figure 1) for the reaction of 2-fluoropropanal, three leading to the (R,S) product (2A-C) and three leading to the (S,S) product (2A’-C’). The lowest energy transition states, 2A and 2A’, both have the fluorine atom positioned anti to the carbonyl, consistent with the Cornforth model. This reflects the stability of 2-fluoropropanal. Similar results are found for addition to 2-chloropropanal
 |
 |
||
|
2A (0.0) |
2B (2.4) |
||
 |
|||
|
2C (2.6) |
|||
|
|
|
||
|
2A’ (0.8) |
2B’ (1.4) |
||
|
|
|||
|
2C’ (3.7) |
|||
Figure 1. Optimized transition states and relative energies (kcal mol-1) for the reaction of 2-fluoropropanal with enolborane computed at B3LYP/6-31G(d).2
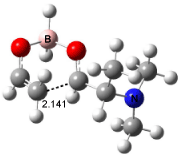
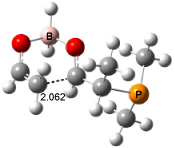
For the reaction of enolborane with 2-methoxypropanal, the lowest energy transition state, 3, also has the methoxy group anti to the carbonyl (see Figure 2). However, the lowest energy transition state for the reaction of 2-methylthiopropanal, 4, has the MeS group perpendicular to the carbonyl, as predicted by the Felkin-Anh model. Similarly, the lowest energy transition states for the addition to 2-dimethylaminopropanal (5) and to 2-dimenthylphosphinopropanal (6) follow the Felkin-Anh model.
The lowest energy conformer of propanal with F, Cl, or OMe as the 2-substituent has the substituent anti to the carbonyl. All three of these aldehydes undergo addition of enolborane through the Cornforth TS. The lowest energy conformer with SMe2 or PMe2 has the substituent perpendicular to the carbonyl, which mimics its location in the enolborane transition state. Only 2-dimethylaminopropanal falls outside this pattern; its lowest energy conformer positions the substituent about 150° from the carbonyl, but rotation to a perpendiculat (Felkin-Anh) position requires only 2 kcal mol-1, half of that need for F, Cl, or methoxy rotation. Cee, Cramer, and Evans draw two conclusions. First, the stereochemistry 1,2-addition of enolborane parallels the conformation of the aldehyde itself, and second, this implies that the Cornforth pathway can be preferred over the Felkin-Anh for those aldehydes where the anti conformation is particularly stable.
 |
 |
||
|
3 |
4 |
||
 |
|
||
|
5 |
6 |
||
References
(1) Frenking, G.; F., K. K.; Reetz, M. T., “On the Origin of π-Facial Diastereoselectivity in Nucleophilic Additions to Chiral Carbonyl Compounds. 2. Calculated Transition State Structures for the Addition of Nucleophiles to Propionaldehyde 1, Chloroacetyldehyde 2, and 2-Chloropropionaldehyde 3.,” Tetrahedron 1991, 47, 9005-9018, DOI: 10.1016/S0040-4020(01)86505-4.
(2) Cee, V. J.; Cramer, C. J.; Evans, D. A., “Theoretical Investigation of Enolborane Addition to α-Heteroatom-Substituted Aldehydes. Relevance of the Cornforth and Polar Felkin-Anh Models for Asymmetric Induction,” J. Am. Chem. Soc. 2006, 128, 2920-2930, DOI: DOI: 10.1021/ja0555670
(3) Evans, D. A.; Siska, S. J.; Cee, V. J., “Resurrecting the Cornforth Model for Carbonyl Addition: Studies on the Origin of 1,2-Asymmetric Induction in Enolate Additions to Heteroatom-Substituted Aldehydes,” Angew. Chem. Int. Ed. 2003, 42, 1761-1765, DOI: 10.1002/anie.200350979.