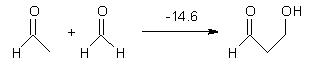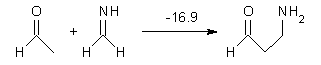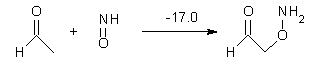Houk has performed a very nice examination of the performance of some density functionals.¹ He takes a quite different approach than what was proposed by Grimme – the “mindless” benchmarking² using random molecules (see this post). Rather, Houk examined a series of simple aldol, Mannich and α-aminoxylation reactions, comparing their reaction energies predicted with DFT against that predicted with CBQ-QB3. The idea here is to benchmark DFT performance for simple reactions of specific interest to organic chemists. These reactions are of notable current interest due their involvement in organocatalytic enantioselective chemistry (see my posts on the aldol, Mannich, and Hajos-Parrish-Eder-Sauer-Wiechert reaction). Examples of the reactions studied (along with their enthalpies at CBS-QB3) are Reaction 1-3.

	Reaction 1
	Reaction 2
	Reaction 3

For the four simple aldol reactions and four simple Mannich reactions, PBE1PBE,
mPW1PW91 and MO6-2X all provided reaction enthalpies with errors of about 2 kcal mol^-1. The much maligned B3LYP functional, along with B3PW91 and B1B95 gave energies with significant larger errors. For the three α-aminoxylation reactions, the errors were better with B3PW91 and B1B95 than with PBE1PBE or MO6-2X. Once again, it appears that one is faced with finding the right functional for the reaction under consideration!

Of particular interest is the decomposition of these reactions into related isogyric, isodesmic
and homdesmic reactions. So for example Reaction 1 can be decomposed into Reactions 4-7 as shown in Scheme 1. (The careful reader might note that these decomposition reactions are isodesmic and homodesmotic and hyperhomodesmotic reactions.) The errors for Reactions 4-7 are typically greater than 4 kcal mol^-1 using B3LYP or B3PW91, and even with MO6-2X the errors are about 2 kcal mol^-1.

Scheme 1.

Houk also points out that Reactions 4, 8 and 9 (Scheme 2) focus on having similar bond changes as in Reactions 1-3. And it’s here that the results are most disappointing. The errors produced by all of the functionals for Reactions 4,8 and 9 are typically greater than 2 kcal mol^-1, and even MO2-6x can be in error by as much as 5 kcal mol^-1. It appears that the reasonable performance of the density functionals for the “real world” aldol and Mannich reactions relies on fortuitous cancellation of errors in the underlying reactions. Houk calls for the development of new functionals designed to deal with fundamental simple bond changing reactions, like the ones in Scheme 2.

Scheme 2

References

(1) Wheeler, S. E.; Moran, A.; Pieniazek, S. N.; Houk, K. N., "Accurate Reaction Enthalpies and Sources of Error in DFT Thermochemistry for Aldol, Mannich, and α-Aminoxylation Reactions," J. Phys. Chem. A 2009, 113, 10376-10384, DOI: 10.1021/jp9058565

(2) Korth, M.; Grimme, S., ""Mindless" DFT Benchmarking," J. Chem. Theory Comput. 2009, 5, 993–1003, DOI: 10.1021/ct800511q

Houk¹ examined the Mannich reaction of the enamine formed from acetone and S-proline with N-ethylidine-N-phenylamine (see Chapter 5.3.3 in my book). Parasuk and Parasuk now extend this to the reaction of the enamine of cyclohexanone and S-proline with N-phenylmethanimine (Reaction 1).² Geometries were optimized at B3LYP/6-31++G(d,p) and single-point energies computed with PCM (for the solvent DMSO) at both B3LYP and MP2.

Reaction 1

First, they examined the formation of the enamine 1, which can be in the syn or anti conformation. The barrier for formation of the syn isomer is 10.2 kcal mol^-1. The barrier for the formation of the anti conformer is much higher, 17.9 kcal mol^-1, and this is with a single water molecule used to assist the proton migration. However, the rotational barrier between the two conformers is only 4.2 kcal mol^-1. So, they conclude that the syn isomer is the only conformer directly formed by the reaction of cyclohexanone and S-proline, and then rotation can produce the anti conformer.

The located the transition state for the reaction of either syn–1 or anti–1 with phenylmethanimine. The two transition states are shown in Figure 1. The barrier for the reaction of syn–1 is 8.5 kcal mol^-1, leading to the S product. The other barrier is higher, 13.0 kcal mol^-1, and the R product 2R is 6.8 kcal mol^-1 higher in energy than the S product 2S. Thus, the reaction to give the S product is both kinetically and thermodynamically favored. This is consistent with experiment³ which gives the S product with 99%ee. Inclusion of solvent makes the S product even more thermodynamically and kinetically favored over the R isomer.

TS-2S

TS-2R

Figure 1. B3LYP/6-311++G(d,p) optimized transition states leading to 2S and 2R.²

References

(1) Bahmanyar, S.; Houk, K. N., "Origins of Opposite Absolute Stereoselectivities in Proline-Catalyzed Direct Mannich and Aldol Reactions," Org. Lett. 2003, 5, 1249-1251, DOI: 10.1021/ol034198e.

(2) Parasuk, W.; Parasuk, V., "Theoretical Investigations on the Stereoselectivity of the Proline Catalyzed Mannich Reaction in DMSO," J. Org. Chem. 2008, 73, 9388-9392, DOI: 10.1021/jo801872w.

(3) Ibrahem, I.; Zou, W.; Casas, J.; Sundén, H.; Córdova, A., "Direct organocatalytic enantioselective α-aminomethylation of ketones," Tetrahedron 2006, 62, 357-364, DOI: 10.1016/j.tet.2005.08.113.

InChIs

1: InChI=1/C11H17NO2/c13-11(14)10-7-4-8-12(10)9-5-2-1-3-6-9/h5,10H,1-4,6-8H2,(H,13,14)/t10-/m0/s1/f/h13
InChIKey=FGOQJKISPWOYSX-WSLRCUSADU

2S: InChI=1/C18H24N2O2/c21-18(22)16-10-6-11-17(16)20-12-5-4-9-15(20)13-19-14-7-2-1-3-8-14/h1-3,7-8,15-16,19H,4-6,9-13H2/b20-17+/t15-,16+/m0/s1
InChIKey=SDMHQUCIHUXJMJ-OQSOEKIEBW

2R: InChI=1/C18H24N2O2/c21-18(22)16-10-6-11-17(16)20-12-5-4-9-15(20)13-19-14-7-2-1-3-8-14/h1-3,7-8,15-16,19H,4-6,9-13H2/b20-17-/t15-,16-/m1/s1
InChIKey=SDMHQUCIHUXJMJ-HGWRPWPUBS