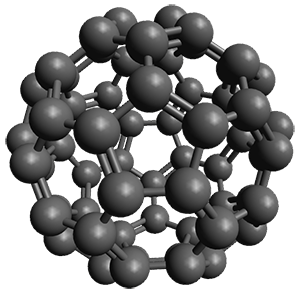
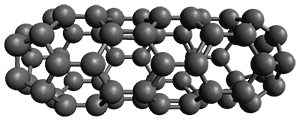
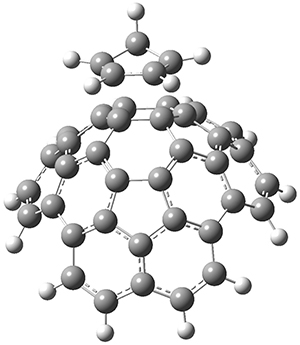
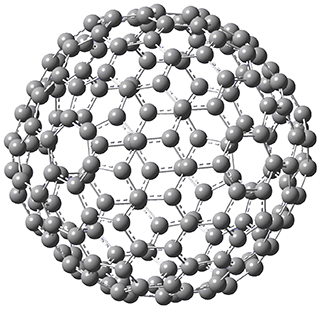
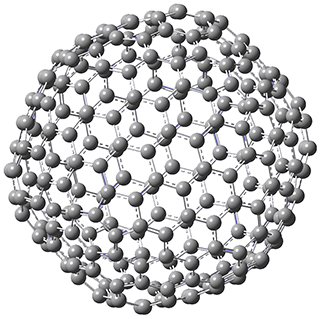
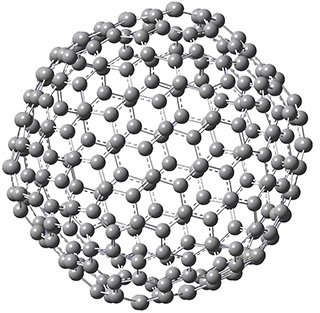
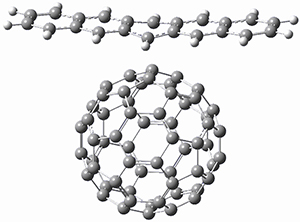
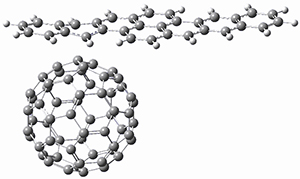
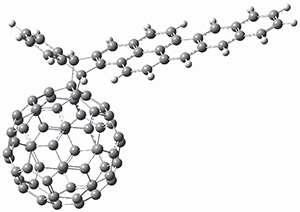
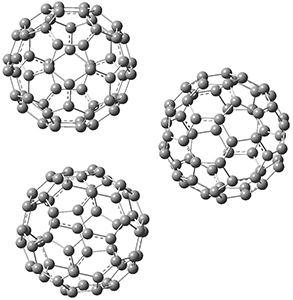
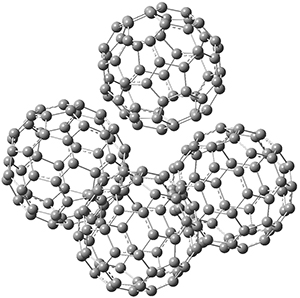
The Grimme group has examined all 1812 C₆₀ isomers, in part to benchmark some computational methods.¹ They computed all of these structures at PW6B95-D3/def2-QZVP//PBE-D3/def2-TZVP. The lowest energy structure is the expected fullerene 1 and the highest energy structure is the nanorod 2 (see Figure 1).

Figure 1. Optimized structures of the lowest (1) and highest (2) energy C₆₀ isomers.

About 70% of the isomers like in the range of 150-250 kcal mol^-1 above the fullerene 1, and the highest energy isomer 2 lies 549.1 kcal mol^-1 above 1. To benchmark some computational methods, they selected the five lowest energy isomers and five other isomers with higher energy to serve as a new database (C60ISO), with energies computed at DLPNO-CCSD(T)/CBS*. The mean absolute deviation of the PBE-D3/def2-TZVP relative energies with the DLPNO-CCSD(T)/CBS* energies is relative large 10.7 kcal mol^-1. However, the PW6B95-D3/def2-QZVP//PBE-D3/def2-TZVP method is considerably better, with a MAD of only 1.7 kcal mol^-1. This is clearly a reasonable compromise method for fullerene-like systems, balancing accuracy with computational time.

They also compared the relative energies of all 1812 isomers computed at PW6B95-D3/def2-QZVP//PBE-D3/def2-TZVP with a number of semi-empirical methods. The best results are with the DFTB-D3 method, with an MAD of 5.3 kcal mol^-1.

References

1) Sure, R.; Hansen, A.; Schwerdtfeger, P.; Grimme, S., "Comprehensive theoretical study of all 1812 C₆₀ isomers." Phys. Chem. Chem. Phys. 2017, 19, 14296-14305, DOI: 10.1039/C7CP00735C.

InChIs

1: InChI=1S/C60/c1-2-5-6-3(1)8-12-10-4(1)9-11-7(2)17-21-13(5)23-24-14(6)22-18(8)28-20(12)30-26-16(10)15(9)25-29-19(11)27(17)37-41-31(21)33(23)43-44-34(24)32(22)42-38(28)48-40(30)46-36(26)35(25)45-39(29)47(37)55-49(41)51(43)57-52(44)50(42)56(48)59-54(46)53(45)58(55)60(57)59
InChIKey=XMWRBQBLMFGWIX-UHFFFAOYSA-N

2: InChI=1S/C60/c1-11-12-2-21(1)31-41-32-22(1)3-13(11)15-5-24(3)34-43(32)53-55-47-36-26-6-16-17-7(26)28-9-19(17)20-10-29-8(18(16)20)27(6)37-46(36)54(51(41)55)52-42(31)33-23(2)4(14(12)15)25(5)35-44(33)58-56(52)48(37)39(29)50-40(30(9)10)49(38(28)47)57(53)59(45(34)35)60(50)58
InChIKey=AGZHNPDQKMDYHI-UHFFFAOYSA-N

Fullerenes can undergo the Diels-Alder reaction with some specificity: the diene preferentially adds across the bond shared by two fused 6-member rings over the bond shared by the fused 6- and 5-member rings. Garcia-Rodeja and colleagues have examined the analogous Diels-Alder reaction of cyclopentadiene with five curved aromatic compounds, 1-5.¹

The computations were performed at BP86-D3/def2-TZVPP//RI-BP86-D3/def2-SVP. Representative transition states for the addition of cyclopentadiene with 3 over the 6,6-bond and 5,6-bond are shown in Figure 1.

5,6-bond

6,6-bond

Figure 1. RI-BP86-D3/def2-SVP optimized transition states for the reaction of cyclopentadiene with 3.

For the reactions of cyclopentadiene with 2-5 the reactions with the 6,6-bond is both kinetically and thermodynamically favored, while with 1 the 6,6-bond is kinetically preffered and the 5,6-adduct is the thermodynamic product. As the molecules increase in size (from 1 to 5), the activation barrier decreases, and the barrier for the reaction with 5 is only 1.4 kcal mol^-1larger than the barrier with C₆₀. The reaction energy also becomes more exothermic with increasing size. There is a very good linear relationship between activation barrier and reaction energy.

Use of the distortion/interaction model indicates that the preference for the 6,6-regioselectivity come from better interaction energy than for the 5,6-reaction, and this seems to come about by better orbital overlap between the cyclopentadiene HOMO and the 6,6-LUMO of the buckybowl.

References

(1) García-Rodeja, Y.; Solà, M.; Bickelhaupt , F. M.; Fernández, I. "Reactivity and Selectivity of Bowl-Shaped Polycyclic Aromatic Hydrocarbons: Relationship to C60," Chem. Eur. J. 2016, 22, 1368-1378, DOI: .

InChIs

1: InChI=1S/C20H10/c1-2-12-5-6-14-9-10-15-8-7-13-4-3-11(1)16-17(12)19(14)20(15)18(13)16/h1-10H
InChIKey=VXRUJZQPKRBJKH-UHFFFAOYSA-N

2: InChIKey=ASIFYFRJNYNQLA-UHFFFAOYSA-N

3: InChI=1S/C26H12/c1-5-13-14-6-2-11-19-20-12-4-8-16-15-7-3-10-18-17(9-1)21(13)25(22(14)19)26(23(15)18)24(16)20/h1-12H
InChIKey=OUWFOTSXASFGQD-UHFFFAOYSA-N

4: InChI=1S/C30H12/c1-2-14-6-10-18-20-12-8-16-4-3-15-7-11-19-17-9-5-13(1)21-22(14)26(18)29(25(17)21)30-27(19)23(15)24(16)28(20)30/h1-12H
InChIKey=JEUCRZPADDQRKU-UHFFFAOYSA-N

5: InChI=1S/C36H12/c1-7-16-17-9-3-14-5-11-20-21-12-6-15-4-10-19-18-8-2-13(1)22-25(16)31-32(26(18)22)34-28(19)24(15)30(21)36(34)35-29(20)23(14)27(17)33(31)35/h1-12H
InChIKey=QMGQDOOJOCPYIA-UHFFFAOYSA-N

What is the size of a molecule that will stretch computational resources today? Chan and co-workers have examined some very large fullerenes¹ to both answer that question, and also to explore how large a fullerene must be to approach graphene-like properties.

They are interested in predicting the heat of formation of large fullerenes. So, they benchmark the heats of formation of C₆₀ using four different isodesmic reactions (Reaction 1-4), comparing the energies obtained using a variety of different methods and basis sets to those obtained at W1h. The methods include traditional functionals like B3LYP, B3PW91, CAM-B3LYP, PBE1PBE, TPSSh, B98, ωB97X, M06-2X3, and MN12-SX, and supplement them with the D3 dispersion correction. Additionally a number of doubly hybrid methods are tested (again with and without dispersion corrections), such as B2-PLYP, B2GPPLYP, B2K-PLYP, PWP-B95, DSD-PBEPBE, and DSD-B-P86. The cc-pVTZ and cc-pVQZ basis sets were used. Geometries were optimized at B3LYP/6-31G(2df,p).

Excellent results were obtained with DSD-PBEPBE-D3/cc-pVQZ (an error of only 1.8 kJ/mol), though even a method like BMK-D3/cc-pVTZ had an error of only 9.2 kJ/mol. They next set out to examine large fullerenes, including such behemoths as C₁₈₀, C₂₄₀, and C₃₂₀, whose geometries are shown in Figure 1. Heats of formation were obtained using isodesmic reactions that compare back to smaller fullerenes, such as in Reaction 5-8.

C180

C240

C320

Figure 1. B3LYP/6-31G(2df,p) optimized geometries of C₁₈₀, C₂₄₀, and C₃₂₀. (Don’t forget that clicking on these images will launch Jmol and allow you to manipulate the molecules in real-time.)

Next, taking the heat of formation per C for these fullerenes, using a power law relationship, they were able to extrapolate out the heat of formation per C for truly huge fullerenes, and find the truly massive fullerenes, like C₉₆₈₀, still have heats of formation per carbon 1 kJ/mol greater than for graphene itself.

References

(1) Chan, B.; Kawashima, Y.; Katouda, M.; Nakajima, T.; Hirao, K. "From C₆₀ to Infinity: Large-Scale Quantum Chemistry Calculations of the Heats of Formation of Higher Fullerenes," J. Am. Chem. Soc. 2016, 138, 1420-1429, DOI: 10.1021/jacs.5b12518.

Capturing buckyballs involves molecular design based on non-covalent interactions. This poses interesting challenges for both the designer and the computational chemist. The curved surface of the buckyball demands a sequestering agent with a complementary curved surface, likely an aromatic curved surface to facilitate π-π stacking interactions. For the computational chemist, weak interactions, like dispersion and π-π stacking demand special attention, particularly density functionals designed to account for these interactions.

Two very intriguing new buckycatchers were recently prepared in the Sygula lab, and also examined by DFT.¹ Compounds 1 and 2 make use of the scaffold developed by Klärner.² In these two buckycatchers, the tongs are corranulenes, providing a curved aromatic surface to match the C₆₀ and C₇₀ surface. They differ in the length of the connector unit.

B97-D/TZVP computations of the complex of 1 and 2 with C₆₀ were carried out. The optimized structures are shown in Figure 1. The binding energies (computed at B97-D/QZVP*//B97-D/TZVP) of these two complexes are really quite large. The binding energy for 1:C₆₀ is 33.6 kcal mol^-1, comparable to some previous Buckycatchers, but the binding energy of 2:C₆₀ is 50.0 kcal mol^-1, larger than any predicted before.

1

2

Figure 1. B97-D/TZVP optimized geometries of 1:C₆₀and 2:C₆₀.

Measurement of the binding energy using NMR was complicated by a competition for one or two molecules of 2 binding to buckyballs. Nonetheless, the experimental data show 2 binds to C₆₀ and C₇₀ more effectively than any previous host. They were also able to obtain a crystal structure of 2:C₆₀.

References

(1) Abeyratne Kuragama, P. L.; Fronczek, F. R.; Sygula, A. "Bis-corannulene Receptors for Fullerenes Based on Klärner’s Tethers: Reaching the Affinity Limits," Org. Lett. 2015, ASAP, DOI: 10.1021/acs.orglett.5b02666.

(2) Klärner, F.-G.; Schrader, T. "Aromatic Interactions by Molecular Tweezers and Clips in Chemical and Biological Systems," Acc. Chem. Res. 2013, 46, 967-978, DOI: 10.1021/ar300061c.

InChIs

1: InChI=1S/C62H34O2/c1-63-61-57-43-23-45(41-21-37-33-17-13-29-9-5-25-3-7-27-11-15-31(35(37)19-39(41)43)53-49(27)47(25)51(29)55(33)53)59(57)62(64-2)60-46-24-44(58(60)61)40-20-36-32-16-12-28-8-4-26-6-10-30-14-18-34(38(36)22-42(40)46)56-52(30)48(26)50(28)54(32)56/h3-22,43-46H,23-24H2,1-2H3/t43-,44+,45+,46-
InChIKey=RLOJCVYXCBOUQB-RYSLUOGPSA-N

2: InChI=1S/C66H36O2/c1-67-65-51-24-45-43-23-44(42-20-38-34-16-12-30-8-4-27-3-7-29-11-15-33(37(38)19-41(42)43)59-55(29)53(27)56(30)60(34)59)46(45)25-52(51)66(68-2)64-50-26-49(63(64)65)47-21-39-35-17-13-31-9-5-28-6-10-32-14-18-36(40(39)22-48(47)50)62-58(32)54(28)57(31)61(35)62/h3-22,24-25,43-44,49-50H,23,26H2,1-2H3/t43-,44+,49+,50-
InChIKey=JAUUHTKCNSNBMD-NETXOKAWSA-N

Diels-Alder reaction involving fullerenes have been known for some time. They occur across the [6,6] double bond of C₆₀, the one between two fused 6-member rings. Houk and Briseno report on the Diels-Alder reaction of C₆₀ with pentacene 1 and bistetracene 2 and compare their computations with experiments.¹

Pentacene and bistetracene ring numbering convention

Computations were performed for the reaction of 1 and 2 with C₆₀ at M06-2x/6-31G(d)//M062x-3-21G*. The reaction can occur with the dienophile being either ring 1, 2, or 3 of pentacene and ring 1, 2, 3, or 4 of bistetracene. They located TSs and products for all of these possibilities. Select TSs and products are shown in Figure 1.

For the reaction of 1a, the lowest energy TS is for the reaction at the central ring (ring 3), and the resulting product is the lowest energy product. The transition state (PT_TS3) is shown in Figure 1. This TS has the least distortion energy of the three possibilities, because reacting at this central ring destroys the least amount of aromaticity of pentacene. For the reaction of 1b, the lowest barrier is again for reaction of ring 3 (through TMSPT_TS3). However, the product from the reaction with ring 2 (TMSPT_P2) is lower in free energy than TMSPT­_P3, likely caused by steric interactions with the silyl substituents. This actually matches up with experiments which indicate that an analogue of TMSPT_P2 is the kinetic product but TMSPT_P3 is the thermodynamic product.

PT_TS3
TMSPT_­TS3
TMSPT_P2	TMSPT_P3
BT_TS2	BT_P2

Figure 1. M06-2x/3-21G* optimized geometries.
(Once again a reminder that clicking on any of these structures will launch JMol and you’ll be able to visualize and manipulate this structure in 3-D.)

The computations involving the Diels-Alder reaction of C₆₀ with either 2a or 2b come to the same conclusion. In both cases, the lowest barrier is for the reaction at ring 2, and the product of the reaction at this same ring is the only one that is endoergonic. The geometries of BT_TS2 and BT_P2 are shown in Figure 1. More importantly, the barrier for the Diels-Alder reaction involving 2a and 2b are at least 6 kcal mol^-1 higher than the barriers for the reaction of 1a and 1b, in complete agreement with experiments that show little reaction involving analogues of 2b with C₆₀, while analogues of 1b are reasonably rapid.

References

(1) Cao, Y.; Liang, Y.; Zhang, L.; Osuna, S.; Hoyt, A.-L. M.; Briseno, A. L.; Houk, K. N. "Why Bistetracenes Are Much Less Reactive Than Pentacenes in Diels–Alder Reactions with Fullerenes," J. Am. Chem. Soc. 2014, 136, 10743-10751, DOI: 10.1021/ja505240e.

Clark and co-workers have examined small fullerene clusters for their ability to capture electrons.¹ They first looked at the fullerene dimer, comparing the electron affinity of the dimer having a C-C bond between the two cages (about 1.6-1.7 Å between the two cages) 1 and where the two cages are interacting only through van der Waals attractions (around 2.6 Å) 2. The structures and their radical anions were computed at RI-BP86/TZV. The structures of the two radical anions are shown in Figure 1. Interestingly, the radical anion of 2 is actually lower in energy that the radical anion of 1. Comparisons with some other methods are discussed, including a CASSPT2(5,4)/ANO-L-VDZ, computation, that support this result.

1	2
3	4

Figure 1. RI-BP86/TZV optimized geometries of the radical anions of 1-4.
(Be sure to click on these images to be able to manipulate these structures in 3-D!)

This suggests that the added electron is being held between the cages, in an interstitial region. That suggested looking at the trimer and tetramer structures 3 and 4. The radical anions of these two oligomers are also shown in Figure 1. These oligomers show electron affinities of 1 eV greater than for fullerene itself, along with the ability to stabilize the dianion and even the trianion, what the authors call “deep electron traps”.

References

(1) Shubina, T. E.; Sharapa, D. I.; Schubert, C.; Zahn, D.; Halik, M.; Keller, P. A.; Pyne, S. G.; Jennepalli, S.; Guldi, D. M.; Clark, T. "Fullerene Van der Waals Oligomers as Electron Traps," J. Am. Chem. Soc. 2014, 136, 10890-10893, DOI: 10.1021/ja505949m.