What happens when anions are sequentially solvated with more and more water? In an interesting study by Chesnovsky, Gerber and coworkers, the answer is proton transfer!¹ They examined the conjugate base of aniline (C₆H₅NH^–, 1) using both PES and MP2/DZP computations. The PES spectrum of 1 shows two strong peaks. When this anion is then coordinates with one or two water molecules, C₆H₅NH^–)^.(H₂O) or (C₆H₅NH^–)^.(H₂O)₂, the peaks shifts to higher energy but the general shape remains unchanged. When three or more water molecules are coordinated to 1, the PE spectra totally changes, becoming broad and relatively featureless.

What accounts for this different PES? The authors posit that the PES of these larger clusters resembles that of hydrated OH^– clusters. Optimization of (C₆H₅NH^–)^.(H₂O) or (C₆H₅NH^–)^.(H₂O)₂
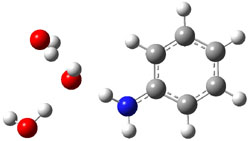
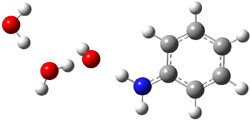
gave structures of the waters hydrogen bonded to the nitrogen anion. However, optimization of the (C₆H₅NH^–)^.(H₂O)₃ gave in fact a cluster of the form (C₆H₅NH₂)^.(HO^–)^.(H₂O)₂. The two lowest energy structures are shown in Figure 1. The structures correspond to the transfer of one proton from water to the anilinide anion to give aniline associated with hydroxide and two water molecules.

Rel E: 0.0

Rel E: 0.10 eV

Figure 1. B3LYP/6-31+G(d) optimized structures of
the C₆H₅NH₂)^.(HO^–)^.(H₂O)₂ clusters.

(Note: Once again the authors have failed to include the computed structures as part of the supporting information and so I have reoptimized the structures but at a lower, computationally more tractable level. Hopefully, authors, editors and reviewers will standardize this practice and include such materials in all papers in the very near future!)

Though aniline is a stronger gas-phase acid than water (DPE(aniline) = 366.4 kcal mol^-1 and DPE(H₂O) = 390.3 kcal mol^-1), the reverse is true in solution (pK_a(aniline) = 27.3) and pK_a(water) = 15.7). As more water molecules are present, the preferential solvation of the hydroxide anion over C₆H₅NH^– results in the formation of hydroxide.

References

(1) Wolf, I.; Shapira, A.; Giniger, R.; Miller, Y.; Gerber, R. B.; Cheshnovsky, O., "Critical Size for Intracluster Proton Transfer from Water to an Anion," Angew. Chem. Int. Ed., 2008, DOI: 10.1002/anie.200800542

Cramer and Truhlar¹ have published a nice review of their SM8 approach to evaluated solvation energy. Besides a quick summary of the theoretical approach behind the model, they detail a few applications. Principle among these is (a) the very strong performance of SM8 relative to some of the standard approaches in the major QM codes (see my previous blog post), (b) modeling interfaces, and (c) computing pK_a values of organic compounds.

References

(1) Cramer, C. J.; Truhlar, D. G., "A Universal Approach to Solvation Modeling," Acc. Chem. Res. 2008, 41, 760-768, DOI: 10.1021/ar800019z.

Bickelhaupt has reported a broad benchmark study of the prototype S_N2 and E2 reactions.¹ These are the reactions of ethyl fluoride with fluoride and ethyl chloride with chloride (Scheme A). The critical points were optimized at OLYP/TZ2P and then CCSD(T)/CBS energies are used as benchmark. A variety of different density functionals were then used to obtain single-point energies.

Scheme A

The relative energies of the transition states for the six different reactions are listed for some of the functionals in Table 1. (These are energies relative to separated reactants – and keep in mind that an ion dipole complex is formed between the reactants and the transition states – Bickelhaupt calls this a “reaction complex”.)

Table 1. Relative energies (kcal mol^-1) of the transition states for the six reactions shown in Scheme A.

There is a lot more data in this paper, along with a summary of the mean absolute errors in the overall and central barriers that mimics the data I show in Table 1. The trends are pretty clear. Generalized gradient approximation (GGA) functions – like BLYP, PW91, and PBE – dramatically underestimate the barriers. The hybrid functionals perform much better. The recently maligned B3LYP functional gets the correct trend and provides reasonable estimates of the barriers. Truhlar’s MO5-2X and MO6-2X functionals do very well in matching up the barrier heights along with getting the correct trends in the relative barriers. Simply looking for the functional with the lowest absolute error is not sufficient; BHandH and MO6-L have small errors but give a wrong trend in barriers, predicting that the S_N2 reaction is preferred over the E2 for the fluoride reaction.

Reference

(1) Bento, A. P.; Sola, M.; Bickelhaupt, F. M., "E2 and S_N2 Reactions of X^– + CH₃CH₂X (X = F, Cl); an ab Initio and DFT Benchmark Study," J. Chem. Theory Comput., 2008, 4, 929-940, DOI: 10.1021/ct700318e.

Schleyer continues his study of aromaticity with a paper¹ that picks up on the theme presented in one² I have previously blogged on – the relationship between a formally aromatic pyrazine and formally antiaromatic dihydropyrazine. He now examines the diazotetracene 1 and it dihydro analogue 2.¹ In terms of formal electron count, 1 should be aromatic, just like the all carbon analogue tetracene 3, and 2 should be antiaromatic.

Schleyer used the NICS_πzz values obtained in the center of each ring to evaluate the aromatic/antiaromatic character of these three molecules. These calculations were performed using canonical molecular orbitals and repeated using localized molecular orbitals. The results are similar for each method, and the canonical MO values are presented in Table 1. As expected for an aromatic compound, each ring of tetracene 3 has large negative NICS values, indicating that each ring is locally aromatic and the molecule as a whole is aromatic. The same is true for the diazotetracene 1. (In fact the NICS values for 1 and 3 are remarkably similar.) However, for 2, the dihydropyrazine ring has a positive NICS values, indicative of a locally antiaromatic ring. While the three phenyl rings have negative NICS values, these absolute values are smaller than for the rings of 1 or 3, indicating an attenuation of their aromaticity. Nonetheless, the sum of the NICS values of 2 is negative, suggesting that the molecule is globally aromatic, though only marginally so. This is due to the antiaromaticity of the dihydropyrazine ring being delocalized to some extent over the entire molecule. Schleyer, concludes that “large 4n π compounds […] are not appreciably destabilized relative to their 4n+2 π congeners.”

Table 1 NICS_πzz (ppm) for each ring of 1-3 and their sum.¹

References

(1) Miao, S.; Brombosz, S. M.; Schleyer, P. v. R.; Wu, J. I.; Barlow, S.; Marder, S. R.; Hardcastle, K. I.; Bunz, U. H. F., "Are N,N-Dihydrodiazatetracene Derivatives Antiaromatic?," J. Am. Chem. Soc., 2008, 130, 7339-7344, DOI: 10.1021/ja077614p.

(2) Miao, S.; Schleyer, P. v. R.; Wu, J. I.; Hardcastle, K. I.; Bunz, U. H. F., "A Thiadiazole-Fused N,N-Dihydroquinoxaline: Antiaromatic but Isolable," Org. Lett. 2007, 9, 1073-1076, DOI: 10.1021/ol070013i

InChIs

1: InChI=1/C18H12/c1-2-6-14-10-18-12-16-8-4-3-7-15(16)11-17(18)9-13(14)5-1/h1-12H

2: InChI=1/C16H10N2/c1-2-6-12-10-16-15(9-11(12)5-1)17-13-7-3-4-8-14(13)18-16/h1-10H

3: InChI=1/C16H12N2/c1-2-6-12-10-16-15(9-11(12)5-1)17-13-7-3-4-8-14(13)18-16/h1-10,17-18H

What is the topology of a molecule made of fused benzene rings? Hopf and co-workers have examined the case where the benzene rings are fused in an ortho arrangement to complete a circle, the so-called [n]circulenes 1_n.¹ They computed the series of [3]- to [20]circulene at B3LYP/6-31G(d).

The most common examples of this class are corannulene 1₅ and coronene 1₆. Hopf finds that the small circulenes, [3]- through [6]circulene, are bowls, consistent with many previous studies.

The larger circulenes fall into two distinct topological categories. [7]circulene through [16]circulene are saddles, as shown in Figure 1a. When the compounds are even larger, namely [17]- through [20]circulene, they adopt a helical topology, as seen in Figure 1b. Unfortunately, Hopf does not supply the optimized geometries; there is no supporting material at all. So I have reoptimized [12]circulene at B3LYP/6-31G(d) and [18]circulene at AM1. It is a real shame that authors do not routinely deposit their structures, that referees do not call out the authors on this, and that editors of journals do not demand full geometrical descriptions of all reported computed structures.

a)	b)
112: [12]circulene	118: [18]circulene

Figure 1. Optimized structures of (a) [12]circulene (B3LYP/6-31G(d)) and (b) [20]circulene (AM1).
Note the hydrogens have been omitted for clarity.

Hopf does not provide a comparison of structures and their energies. For example, what is the energy difference between the bowl and saddle topologies of [7]circulene or the energy difference between the saddle and helical topologies of [17]circulene?

The change in topology of the circulenes is fascinating. One wonders if this change is strictly a function of a stringing fused hexagons in a circle and minimizing the surface. Or is their some π-π stacking that leads to the saddle and helical topologies? Further details would be interesting – as would be examining other types of ciculenes as hinted by the authors at the end of the paper regarding isomeric kekulenes 2.

References

(1) Christoph, H.; Grunenberg, J.; Hopf, H.; Dix, I.; Jones, P. G.; Scholtissek, M.; Maier, G., "MP2 and DFT Calculations on Circulenes and an Attempt to Prepare the Second Lowest Benzolog, [4]Circulene," Chem. Eur. J. 2008, 14, 5604-5616, DOI: 10.1002/chem.200701837

InChIs

1₅: InChI=1/C20H10/c1-2-12-5-6-14-9-10-15-8-7-13-4-3-11(1)16-17(12)19(14)20(15)18(13)16/h1-10H
InChIKey: VXRUJZQPKRBJKH-UHFFFAOYAF

1₆: InChI=1/C24H12/c1-2-14-5-6-16-9-11-18-12-10-17-8-7-15-4-3-13(1)19-20(14)22(16)24(18)23(17)21(15)19/h1-12H
InChIKey: VPUGDVKSAQVFFS-UHFFFAOYAQ

1₁₂: InChIKey: FTLFLCQEVCSDMZ-UHFFFAOYAB

1₁₈: InChIKey: CRXJHICCESJVIG-UHFFFAOYAJ