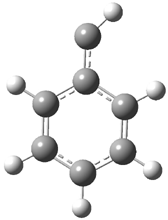
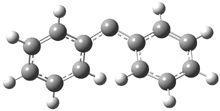
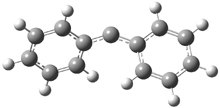
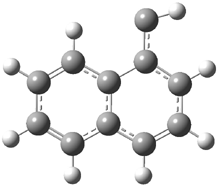
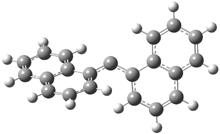
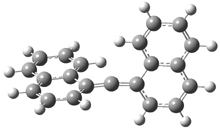
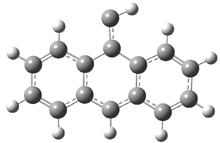
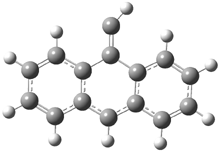
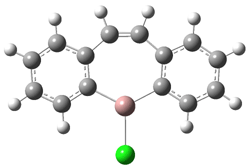
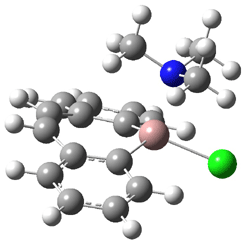
In the book I extensively discuss the singlet-triplet gap of methylene and some of the chemistry of phenylcarbene. Schleyer and Schaefer have now reported computations on the singlet-triplet gap of arylcarbenes.¹ The geometries of phenylcarbene 1, diphenylcarbene 2, 1-naphthylcarbene 3, bis(1-naphtyl)carbene 4, and 9-anthrylcarbene 5 were optimized at B3LYP/6-311+G(d,p). These geometries are shown in Figure 1.

1s	1t
2s	2t
3s	3t
4s	4s
4s	4s

Figure 1. B3LYP/6-311+G(d,p) optimized structures of singlet and triplet 1-5.

Since this functional is known to underestimate the singlet-triplet gap of carbenes, they employ an empirical correction based on the difference in this gap for methylene between the computed value (11.89 kcal mol^-1) and the experimental value (9.05 kcal mol^-1). These corrected energy gaps are listed in Table 1.

Table 1. Corrected singlet-triplet energy gaps (kcal mol^-1) at B3LYP/6-311+G(d,p).

Molecule	ΔEST
1	2.75
2	2.94
3	3.40
4	3.74
5	5.67

Using the following isodesmic reactions, they estimate the stabilization of the singlet or triplet carbene afforded by the aryl substituent:

R-C-H + CH₄ → H-C-H + R-CH₃

R-C-R + CH₄ → R-C-H + R-CH₃

These isodesmic energies are listed in Table 2. For phenylcarbne, the phenyl group stabilizes the singlet more than the triple, reducing the ST gap by 6.3 kcal mol^-1. However, adding a second phenyl group (making 2) stabilizes both the singlet and triplet by about the same amount, leading to little change in the ST gap. The singlet does not get accrue the potential benefit of the second aryl group because sterics prohibit the two rings from being coplanar.

Table 2. Aryl effect for 1-5 based on the isodesmic reaction energies (kcal mol^-1)

Molecule	ΔEsinglet	ΔEtriplet
1	24.4	18.1
2	15.8	16.0
3	26.6	20.9
4	18.6	19.0
5	30.5	26.8

References

(1) Woodcock, H. L.; Moran, D.; Brooks, B. R.; Schleyer, P. v. R.; Schaefer, H. F., "Carbene Stabilization by Aryl Substituents. Is Bigger Better?," J. Am. Chem. Soc., 2007, 129, 3763-3770, DOI: 10.1021/ja068899t.

InChIs

1: InChI=1/C7H6/c1-7-5-3-2-4-6-7/h1-6H

2: InChI=1/C13H10/c1-3-7-12(8-4-1)11-13-9-5-2-6-10-13/h1-10H

3: InChI=1/C11H8/c1-9-5-4-7-10-6-2-3-8-11(9)10/h1-8H

4: InChI=1/C21H14/c1-2-8-19-14-16(12-13-17(19)6-1)15-20-10-5-9-18-7-3-4-11-21(18)20/h1-14H

5: InChI=1/C15H10/c1-11-14-8-4-2-6-12(14)10-13-7-3-5-9-15(11)13/h1-10H

Robinson and Schleyer report the synthesis of and computations on the novel structure gallepin 1.¹ This is the gallium analogue of tropyllium, the prototype of a seven-member aromatic ring. Robinson actually prepared the bis-benzannulated analogue 2, which is found to coordinate to TMEDA in the crystal.

Schleyer computed (B3LYP/LANL2DZ) the gallepin portion of 2 in its naked form 3 and associated with trimethylamine 4. The crystal structure of 2 reveals that the 7 member ring is boat-shaped, and this is reproduced in the computed structure of 4. Interestingly, the naked gallepin is planar, suggestive of an aromatic structure. NICS_πZZ computations were performed to gauge the aromaticity of these compounds. The value for the 7-member ring is -9.0 in 4 and -9.9 in 3, indicating aromatic character. These values are less then in the parent gallepin 1, which has a value of -15.3, but this is the normal type of diminishment expected from benzannulation.
But borapin has a NICS_πZZ substantially more negative (-27.7) and so gallepins are less aromatic than borapins. Nonetheless, it is very interesting that aromaticity can be extended in this interesting way – different heteroatom and different ring size.

3	4

References

(1) Quillian, B.; Wang, Y.; Wei, P.; Wannere, C. S.; Schleyer, P. v. R.; Robinson, G. H., "Gallepins. Neutral Gallium Analogues of the Tropylium Ion: Synthesis, Structure, and Aromaticity," J. Am. Chem. Soc., 2007, 129, 13380-13381, DOI: 10.1021/ja075428d.

In Chapter 7.3.5.1 I discuss the computational and experimental results of Singleton¹ regarding C₂-C₆ enyne allene cyclization. The reaction is shown below, and though Singleton could locate no transition state that connects the reactant to the diradical, molecular dynamics trajectory calculations show that the diradical is sampled, though the dominant pathway is the concerted route.

Schmittel has expanded on this work by determining the kinetic isotope effects for four more analogues.2 The results are summarized in Table 1. Depending on the substituent, the predominant pathway can be concerted or stepwise or even a mixture of these two (termed “boundary”). Schmittel argues that the region about the single transition state, the one that directly connect reactant to product through a concerted path, is actually quite flat. This is a “broad transition state zone”. Trajectories can traverse through various regions of the zone, some that go on to diradical, some that go on to product. Substituents can alter the shape of the TS zone and thereby shift the set of trajectories in one direction or the other. The upshot is further support for the importance on non-statistical dynamics in dictating the course of reactions.

Table 1. Kinetic isotope effects for C₂-C₆ enyne allene cyclizations

Compound	KIE	Prevailing mechanism
R=TMS, R’=H, R”=TMS, Y=OAc	1.431	concerted
R=TMS, R’=iPr, R”=TMS, Y=H	1.60	concerted
R=tBu, R’=iPr, R”=TMS, Y=H	1.24	Boundary
R=TIPS, R’=iPr, R”=p-An, Y=H	1.17	stepwise
R=TMS, R’=iPr, R”=p-An, Y=H	1.08	stepwise

References

(1) Bekele, T.; Christian, C. F.; Lipton, M. A.; Singleton, D. A., ""Concerted" Transition State, Stepwise Mechanism. Dynamics Effects in C²-C⁶ Enyne Allene Cyclizations," J. Am. Chem. Soc. 2005, 127, 9216-9223, DOI: 10.1021/ja0508673.

(2) Schmittel, M.; Vavilala, C.; Jaquet, R., "Elucidation of Nonstatistical Dynamic Effects
in the Cyclization of Enyne Allenes by Means of Kinetic Isotope Effects," Angew. Chem. Int. Ed. 2007, 46, 6911-6914, DOI: 10.1002/anie.200700709