Li and Danishefsky report a study of the Diels-Alder reaction involving cyclobutenone 1 as the dienophile.¹ They claim that “perhaps the ring strain of 1 might well serve to enhance its dienophilicity relative to corresponding cyclopentenones or cyclohexenones.” In fact, 1 is an excellent dienophile, with reactions at or below 0° being accomplished in less than half a day with yields upwards of 90%. The reaction goes with endo selectivity.

What is surprising to me is the statement in the article:

While the magnitude of the effect could not have been predicted in advance, the rate enhancement with 1 must reflect the favorable effects of rehybridization of two particularly strained sp² carbons in the cycloaddition transition state.

Now, Danishefsky alludes to upcoming computations results in a future paper, but I don’t see why the rate enhancement could not have been “predicted in advance”. So, I have optimized the structures of reactants, endo and exo transition states, and products of the reaction of 1,3-butadiene with 1, cyclopentenone 2 and cyclohexenone 3 at B3LYP/6-311G(d) – Reactions 1-3.

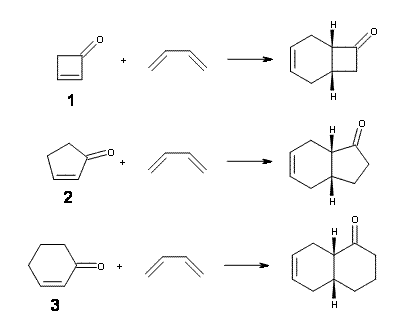
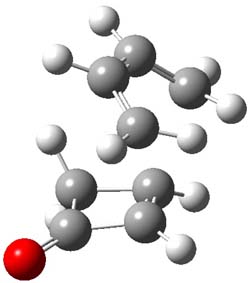
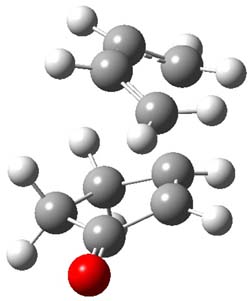
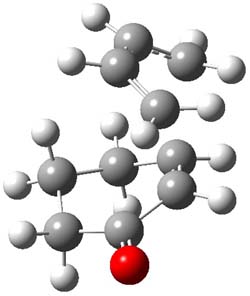
The endo TS is preferred for the reaction of 1 and 2, while the endo and exo TSs for 3 are essentially isoenergetic. The optimized geometries are shown in Figure 1.

1TSendo

2TSendo

3TSendo

Figure 1. B3LYP/6-311G(d) optimized geometries of the endo TSs of Reactions 1-3.

The computed activation barriers and overall reaction energies are listed in Table 1. Clearly, the cycloaddition of 1 is favored both in terms of kinetics (having the lowest barrier) and thermodynamically (having the most exothermic reaction energy). In fact, the reaction barriers increases in going from 1 to 2 to 3 and the exothermicity decreases in that same order. This nicely dovetails with the strain energies of the dienophiles and the fact that cyclopententones and cyclohexenones are generally poor dienophiles. Thus, one clearly could have predicted these results in advance!

Table 1. Activation and Reaction Energy (kcal mol^-1) for Reactions 1-3.

Reaction	Ea	ΔE
1	18.8	-35.2
2	24.1	-27.1
3	25.7	-27.1

Nonetheless, the experimental work is extremely nice and this work offers a new avenue into some interesting bicyclic structures.

Note: This post has been modified to correct the errors in the product structures and their associated InChIs and InChIKeys.

References

(1) Li, X.; Danishefsky, S. J., "Cyclobutenone as a Highly Reactive Dienophile: Expanding Upon Diels-Alder Paradigms," J. Am. Chem. Soc., 2010, 132, 11004-11005, DOI: 10.1021/ja1056888

InChIs

1: InChI=1/C4H4O/c5-4-2-1-3-4/h1-2H,3H2
InChIKey=DFLRGCFWSRELEL-UHFFFAOYAP

1prod: InChI=1/C8H10O/c9-8-5-6-3-1-2-4-7(6)8/h1-2,6-7H,3-5H2/t6-,7-/m0/s1
InChIKey=AYXQRXAAJYZWJJ-BQBZGAKWBC

2: InChI=1/C5H6O/c6-5-3-1-2-4-5/h1,3H,2,4H2
InChIKey=BZKFMUIJRXWWQK-UHFFFAOYAH

2prod: InChI=1/C9H12O/c10-9-6-5-7-3-1-2-4-8(7)9/h1-2,7-8H,3-6H2/t7-,8-/m0/s1
InChIKey=LOJATDUUSCWAOA-YUMQZZPRBU

3: InChI=1/C6H8O/c7-6-4-2-1-3-5-6/h2,4H,1,3,5H2
InChIKey=FWFSEYBSWVRWGL-UHFFFAOYAT

3prod: InChI=1/C10H14O/c11-10-7-3-5-8-4-1-2-6-9(8)10/h1-2,8-9H,3-7H2/t8-,9-/m0/s1
InChIKey=LFDGSLNQYSSFGI-IUCAKERBBQ

The α-proton of ketones and aldehydes are acidic, thanks to delocalization of the resulting anion. However, α-protons at a bridgehead position are much less acidic – the resulting anion is not delocalized as the enolate would be an anti-Bredt alkene. So, what about more remote protons from the carbonyl – would they exhibit enhanced acidity due to inductive or field effects?

Kass has examined the deprotonation of 2-adamantone 1 via experiment and computation.¹ The relative energies of the five different anions are listed in Table 1. Previous H/D exchange experiments indicate that the relative reactivity is β_ax > β_eq > α, and this is well reproduced by computations.²

Table 1. Relative energies (kcal mol^-1) of the enolates of 1.

compound	M06-2x/aug-cc-pVDZ	G3
α	4.27	5.60
βax	0.0	0.0
βeq	4.46
γ	2.28	3.40
δ	6.17	7.55
2	-1.58	0.56

Kass’ bracketing experiments indicate the enthalpy for deptrotonation of 2-adamantone is 394.7 ± 1.4 kcal mol^-1. This is in nice accord with the computational results for loss of the β_ax proton: 393.8 (M06-2x/aug-cc-pVDZ) and 396.8 kcla mol^-1 (G3). One interesting computational result is a competive cyclic structure 2, whose stability is similar to that to the β_ax ion at M06-2x and is the optimized structure produced at MP2/6-31G(d) when searching for the β_eq enolate.

So, to answer our question, protons remote from a carbonyl are more acidic than alkane
analogues, but much less acidic than typical α-protons of ketones.

References

(1) Meyer, M. M.; Kass, S. R., "Enolates in 3-D: An Experimental and Computational Study of Deprotonated 2-Adamantanone," J. Org. Chem., 2010, 75, 4274-4279, DOI: 10.1021/jo100953y

(2) Stothers, J. B.; Tan, C. T., "Adamantanone: stereochemistry of its homoenolization as shown by ²H nuclear magnetic resonance," J. Chem. Soc., Chem. Commun., 1974, 738-739, DOI: 10.1039/C39740000738

InChI

1: InChI=1/C10H14O/c11-10-8-2-6-1-7(4-8)5-9(10)3-6/h6-9H,1-5H2
InChIKey=IYKFYARMMIESOX-UHFFFAOYAE

2: InChI=1/C10H13O/c11-10-7-2-5-1-6(4-7)9(10)8(10)3-5/h5-9H,1-4H2/q-1
InChIKey=WTXOXRNASCZDME-UHFFFAOYAE

I recently finished reading a book on the application of information theory to “reality”: Decoding Reality by Vlatko Vedral. It’s for the layman (me!) and I was wondering what applications have information theory made in chemistry. Well, just by accident I happened upon a paper by Noorizadeh which proposes an information-based metric to evaluate aromaticity!¹ (I know what you’re thinking – we need another aromaticity metric like we need another hole in the head.) I don’t want to suggest that this metric, which he calls “Shannon aromaticity” after the inventor of information theory, will substitute for previous ones (like aromatic stabilization energy or NICS). But the application here is interesting.

Shannon defined entropy in the information sense as

S(r) = -Σ p_i ln p_i

Where p_i is the probability of occurrence i. This can be converted into a quantum analogue as

S[ρ] = -∫ρ(r)  ln ρ(r) dr.

Noorizadeh suggests evaluating the electron density at the bond critical points of an aromatic ring and then summing the values of S at each of these ring critical points. An ideal aromatic ring would have S_max= ln (N) where N is the number of bonds in the ring. So, the Shannon aromaticity (SA) is then defined as the difference between the maximum value (ln (N)) and the sum over the ring critical points. A small value would indicate an aromatic ring, and a large value would indicate an antiaromatic ring.

The paper shows a strong correlation exists between the new SA metric and the warhorses ASE and NICS and HOMA for a variety of aromatic, antiaromatic and non-aromatic systems. This new metric is easy to compute and perhaps offers a new way to be thinking about a very old concept: aromaticity.

References

(1) Noorizadeh, S.; Shakerzadeh, E., "Shannon entropy as a new measure of aromaticity, Shannon aromaticity," Phys. Chem. Chem. Phys., 2010, 12, 4742-4749, DOI: 10.1039/b916509f.