Professor Amnon Stanger sent me an email with a couple of comments concerning points made in my book. I take up the first of his comments here. Stanger has pointed me to what looks to be the true first study evaluating NICS on a grid of points, done by Klod and Kleinpeter in 2001.¹ They computed NICS values on a 3-D grid and then created iso-chemical-shielding surfaces to pictorially represent the shielding and deshielding zones (or cones) created by π-bonds (like ethane and ethyne) and aromatic compounds. In a similar vein, Lazzeretti² evaluated the out-of-plane component of the magnetic shielding tensor (σ_||) on a 2-D grid to demonstrate the shielding and deshielding zones of π-systems, particularly aromatic systems. These plots clearly demonstrate the “cones” one typically finds in introductory organic texts to explain NMR effects.

(1) Klod, S.; Kleinpeter, E., “Ab Initio Calculation of the Anisotropy Effect of Multiple Bonds and the Ring Current Effect of Arenes—Application in Conformational and Configurational Analysis,” Chem. Soc., Perkin Trans. 2, 2001, 1893-1898, DOI: 0.1039/b009809o.

(1) Viglione, R. G.; Zanasi, R.; Lazzeretti, P., “Are Ring Currents Still Useful to Rationalize the Benzene Proton Magnetic Shielding?,” Org. Lett., 2004, 6, 2265-2267, DOI: 10.1021/ol049200w.

I did not present π-π stacking in the book, but I think if I ever do a second edition, I will include a discussion of it. I’m not sure quite where it would fit in given the current structure of the book (I discuss DNA bases and base pairs in the context of solvation in Chapter 6), but the paper I will discuss next gives me some idea – π-π stacking is a sensitive test of the quality of computational methods and this could be part of Chapter 1 as a discussion of the failings of methods, especially DFT.

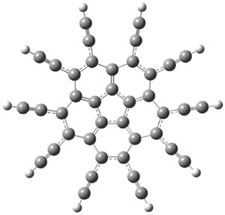
Swart and Bickelhaupt have examined a series of π-π stacked pairs, evaluating them regarding how DFT performs.¹ Their first example is the benzene dimer (Table 1). At CCSD(T) the dimer binding energy is 1.7 kcal mol^-1 and the rings are 3.9 Å apart. LDA, KT1 (yet another newly minted functional^2,3), and BHandH get the separation and binding energy reasonably well. PW91 gets the distance too big and underestimates the binding energy. But most important is that the other (more traditional) functionals indicate that the PES is entirely repulsive! This is a manifestation of many functionals’ inability to properly account for dispersion.

Table 1. Optimized separation distance (r_min, Å) and binding energy (kcal mol^-1)
of the benzene dimer using the TZ2P basis set.¹

Next, they compare 14 different orientations of stacked dimmers of cytosine. The energies of these dimmers were computed using again a variety of functionals and compared to MP2/CBS energies with a correction for CCSD(T). The mean absolute deviations (MAD) for the energies using the various functionals are listed in Table 2. Again, LDA and KT1 perform quite well, but most functionals do quite poorly.

Table 2. Mean absolute deviations of the energies of 14 cytosine
stacked dimer structures compared to their MP2 energies.

Similar results are also demonstrated for stacked DNA bases and also stacked base pairs. These authors conclude that the KT1 functional appears suitable for treating π-π stacking. One should also consider some of the new functionals from the Truhlar group,^4-6 which unfortunately are not included in this study.

References

(1) Swart, M.; van der Wijst, T.; Fonseca, C.; Bickelhaput, F. M., "π-π Stacking Tackled with Density Functional Theory," J. Mol. Model. 2007, 13, 1245-1257, DOI: 10.1007/s00894-007-0239-y.

(2) Keal, T. W.; Tozer, D. J., "The Exchange-Correlation Potential in Kohn–Sham Nuclear Magnetic Resonance Shielding Calculations," J. Chem. Phys. 2003, 119, 3015-3024, DOI: 10.1063/1.1590634

(3) Keal, T. W.; Tozer, D. J., "A Semiempirical Generalized Gradient Approximation Exchange-Correlation Functional," J. Chem. Phys. 2004, 121, 5654-5660, DOI: 10.1063/1.1784777.

(4) Zhao, Y.; Truhlar, D. G., "A Density Functional That Accounts for Medium-Range Correlation Energies in Organic Chemistry," Org. Lett. 2006, 8, 5753-5755, DOI: 10.1021/ol062318n

(5) Zhao, Y.; Schultz, N. E.; Truhlar, D. G., "Design of Density Functionals by Combining the Method of Constraint Satisfaction with Parametrization for Thermochemistry, Thermochemical Kinetics, and Noncovalent Interactions," J. Chem. Theory Comput., 2006, 2, 364-382, DOI: 10.1021/ct0502763.

(6) Zhao, Y.; Truhlar, D. G., "Assessment of Model Chemistries for Noncovalent Interactions," J. Chem. Theory Comput. 2006, 2, 1009-1018, DOI: 10.1021/ct060044j

Truhlar and Cramer have updated their Solvation Model to SM8.¹ This model allows for any solvent to be utilized (both water and organic solvents) and treats both neutral and charged solutes. While there are some small theoretical changes to the model, the major change is in how the parameters are selected, the number of parameters, and a much more extensive data set is used for the fitting procedure.

Of note is how well this new model works. Table 1 compares the errors in solvation free energies computed using the new SM8 model against some other popular continuum methods. Clearly, SM8 provides much better results. As they point out, what is truly discouraging is the performance of the 3PM model against the continuum methods. 3PM stands for “three-parameter model”, where the solvation energies of all the neutral solute in water is set to their average experimental value (-2.99 kcal mol^-1), and the same for the neutral solutes in organic solvents (-5.38 kcal mol^-1), and for ions (-65.0 kcal mol^-1). The 3PM outperforms most of the continuum methods!

Table 1. Mean unsigned error (kcal mol^-1) for the solvation
free energies computed with different methods.¹

^a274 data points. ^b666 data points spread among 16 solvents. ^c332 data points spread among acetonitrile, water, DMSO, and methanol. ^dUsing mPW1PW/6-31G(d). ^eUsing mPW1PW/6-31G(d) and the UA0 atomic radii in Gaussian. ^fUsing mPW1PW/6-31G(d) and the UAHF atomic radii in Gaussian. ^gUsing B3LYP/6-31G(d) and conductor-PCM in GAMESS. ^hUsing B3LYP/6-31G(d) and the PB method in Jaguar.

References

(1) Marenich, A. V.; Olson, R. M.; Kelly, C. P.; Cramer, C. J.; Truhlar, D. G., "Self-Consistent Reaction Field Model for Aqueous and Nonaqueous Solutions Based on Accurate Polarized Partial Charges," J. Chem. Theory Comput., 2007, 3, 2011-2033. DOI: 10.1021/ct7001418.

Poutsma has followed up on the work he reported earlier in collaboration with Kass concerning the gas-phase acidity of the amino acids.¹ Their previous work reported on cysteine,² with the unusual result that the thiol group is more acidic than the carboxylic acid group. (I blogged on this a previous post.) Now, he reports the experimental and DFT acidities of all 20 amino acids, shown in Table 1. The experiments were done using the kinetic method in a quadrupole ion trap with electrospray ionization. The computations were performed at B3LYP/6-311++G**//B3LYP/6-31+G*, following some MM searching to identify low-lying conformations. The computed acidities were obtained relative to acetic acid, i.e. R-CH₂COOH + OAc^– → R-CH₂COO^– +HOAc.

Table 1. Relative acidities (kJ mol^-1) of the amino acids¹

The computed values are in very good agreement with the experimental values. The amino acids are ordered in increasing acidity in Table 1. The order predicted by experiment and DFT are quite close, and the disagreements are well within the error bar of the experiment.

Similar to the result for cysteine, tyrosine also displays unusual acidity. The alcohol proton is more acidic than the carboxylic acid proton. The structures of tyrosine, and its two conjugate
bases, one from loss of the phenolic proton and the other from loss of the carboxylic acid proton are shown in Figure 1. The stability of the tyrosine conjugate base from loss of the phenolic
hydrogen arises from both the stability of phenoxide and the internal hydrogen bond from the carboxylic acid proton to the amine. This is different that in the cysteine case, the thiolate anion is stabilized by an internal hydrogen bond from the carboylic acid group (see Figure 2c here).

tyrosine
Tyrosine conjugate base (loss of phenolic hydrogen)	Tyrosine conjugate base (loss of carboxylate hydrogen)

Figure 1. B3LYP/6-31G* optimized structures of tyrosine and its conjugate bases.¹

References

(1) Jones, C. M.; Bernier, M.; Carson, E.; Colyer, K. E.; Metz, R.; Pawlow, A.; Wischow, E. D.; Webb, I.; Andriole, E. J.; Poutsma, J. C., "Gas-Phase Acidities of the 20 Protein Amino Acids," Int. J. Mass Spectrom. 2007, 267, 54-62, DOI: 10.1016/j.ijms.2007.02.018.

(2) Tian, Z.; Pawlow, A.; Poutsma, J. C.; Kass, S. R., "Are Carboxyl Groups the Most Acidic Sites in Amino Acids? Gas-Phase Acidity, H/D Exchange Experiments, and Computations on Cysteine and Its Conjugate Base," J. Am. Chem. Soc. 2007, 129, 5403-5407, DOI: 10.1021/ja0666194.

InChI

Tyrosine: InChI=1/C9H11NO3/c10-8(9(12)13)5-6-1-3-7(11)4-2-6/h1-4,8,11H,5,10H2,(H,12,13)/t8-/m0/s1

In their continuing efforts to build novel aromatic systems, Siegel and Baldridge report the preparation of the decapropyl analogue of the per-ethynylated corrannulene 1.¹ They were hoping that this might cyclize to the bowl 2. It is however stable up to 100 °C, however, the analogue 3 was obtained in the initial preparation of decapropyl-1.

The B3LYP/cc-pVDZ optimized structures of 1 and 3 are shown in Figure 1. 1 is bowl-shaped, reflecting the property of corranulene, but interestingly 3 is planar. The geometry of the {10]annulene is interesting as it is more consistent with the alkynyl resonance form B.

1

3

Figure 1. B3LYP/cc-pVDZ optimized structures of 1 and 3.¹

Siegel and Baldridge speculate that the conversion of 1 → 3 occurs by first undergoing the Bergman cyclization to give 4, which then opens to give 3. Unfortunately, they did not compute the activation barrier for this process. They do suggest that further cyclization to give the hoped for 2 might be precluded by the long distances between radical center and neighboring alkynes in 4, but the radicals are too protected to allowing trapping by the solvent, allowing for the formation of 3.

References

(1) Hayama, T.; Wu, Y. T.; Linden, A.; Baldridge, K. K.; Siegel, J. S., "Synthesis, Structure, and Isomerization of Decapentynylcorannulene: Enediyne Cyclization/Interconversion of C₄₀R₁₀ Isomers," J. Am. Chem. Soc., 2007, 129, 12612-12613 DOI: 10.1021/ja074403b.

InChIs

1: InChI=1/C40H10/c1-11-21-22(12-2)32-25(15-5)26(16-6)34-29(19-9)30(20-10)35-28(18-8)27(17-7)33-24(14-4)23(13-3)31(21)36-37(32)39(34)40(35)38(33)36/h1-10H

2: InChI=1/C40H10/c1-2-12-14-5-6-16-18-9-10-20-19-8-7-17-15-4-3-13-11(1)21-22(12)32-24(14)26(16)34-29(18)30(20)35-28(19)27(17)33-25(15)23(13)31(21)36-37(32)39(34)40(35)38(33)36/h1-10H

3: InChI=1/C40H12/c1-9-23-25(11-3)33-27(13-5)29(15-7)35-30(16-8)28(14-6)34-26(12-4)24(10-2)32-22-20-18-17-19-21-31(23)36-37(32)39(34)40(35)38(33)36/h1-8,17-18,31-32H/b18-17-

A review of my book Computational Organic Chemistry has appeared in the Journal of the American Chemical Society (DOI: 10.1021/ja077005h) The review by Donald E. Elmore of Wellesley College is very complimentary, pointing out many of the objectives I had hoped to achieve. Nonetheless, I am a bit disappointed in that he did not mention two of the more novel aspects of the book.

I am grateful that Elmore did mention the incorporation of the interviews with six leading theoreticians. However, he failed to mention the ancillary web site and this blog. Both of these electronic resources, I feel, greatly enhance the book. The ancillary web site includes links to all of the literature cited in the test, along with 3-D coordinates of all of the molecules with JMol for visualizing these structures. The blog provides a means for me to maintain the currency of the book. Blog posts extend the coverage of the book’s topics to the latest published research.

Is Elmore’s oversight reflective of a widespread belief that web enhancements offer little value to readers? Am I mistaken in believing that the web offers real opportunities to enhance a book (not just mine!)? I don’t view these web add-ons as “trivial” or “cute” or “trendy”.

I still believe that books offer many advantages to readers and scientists. But there are also limitations to what can be done on the printed page. I had hoped that the coupling of the printed book and the web enhancements would deliver the best of both worlds to my readers. I would enjoy hearing from you about whether these web resources are of value and if not, how do they fail? Are there other web-enabled resources I should explore?