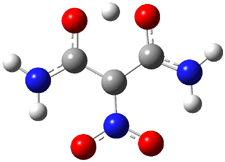
A 2013 study of oxalic acid 1 failed to uncover any tunneling between its conformations,¹ despite observation of tunneling in other carboxylic acids (see this post). This was rationalized by computations which suggested rather high rearrangement barriers. Schreiner, Csaszar, and Allen have now re-examined oxalic acid using both experiments and computations and find what they call domino tunneling.²

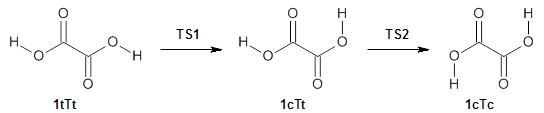
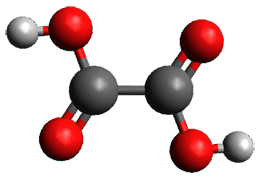
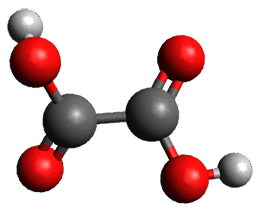
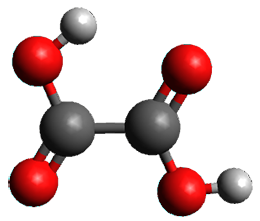
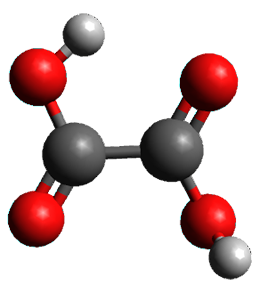
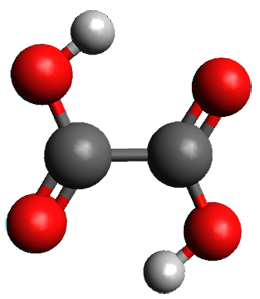
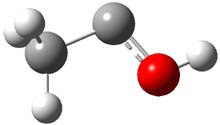
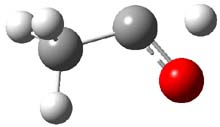
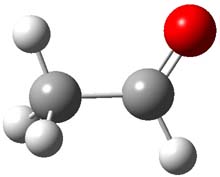
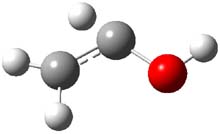
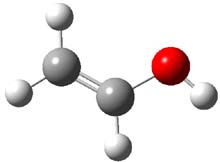
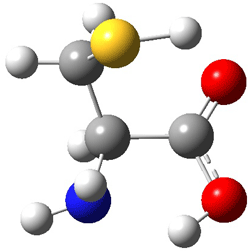
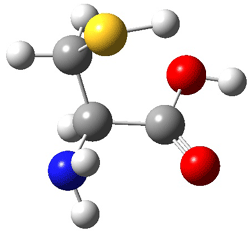
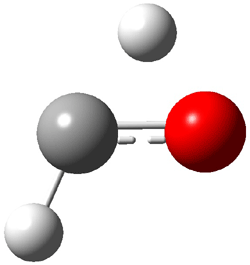
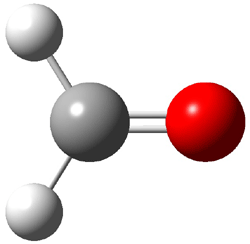
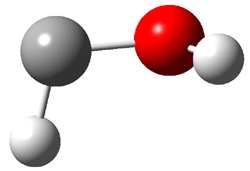
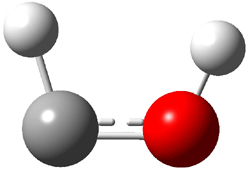
First, they determined the structures of the three conformations of 1 along with the two transition states interconnecting them using the focal point method. These geometries and relative energies are shown in Figure 1. The barrier for the two rearrangement steps are smaller than previous computations suggest, which suggests that tunneling may be possible.

1tTt (0.0)	TS1 (9.7)
1cTt (-1.4)	TS2 (9.0)
1cTc (-4.0)

Figure 1. Geometries of the conformers of 1 and the TS for rearrangement and relative energies (kcal mol^-1)

Placing oxalic acid in a neon matrix at 3 K and then exposing it to IR radiation populates the excited 1tTt conformation. This state then decays to both 1cTt and 1cTc, which can only happen through a tunneling process at this very cold temperature. Kinetic analysis indicates that there are two different rates for decay from both 1tTt and 1cTc, with the two rates associated with different types of sites within the matrix.

The intrinsic reaction paths for the two rearrangements: 1tTt → 1cTt and → 1cTc were obtained at MP2/aug-cc-pVTZ. Numerical integration and the WKB method yield similar half-lives: about 42 h for the first reaction and 23 h for the second reaction. These match up very well with the experimental half-lives from the fast matrix sites of 43 ± 4 h and 30 ± 20 h, respectively. Thus, the two steps take place sequentially via tunneling, like dominos falling over.

References

(1) Olbert-Majkut, A.; Ahokas, J.; Pettersson, M.; Lundell, J. "Visible Light-Driven Chemistry of Oxalic Acid in Solid Argon, Probed by Raman Spectroscopy," J. Phys. Chem. A 2013, 117, 1492-1502, DOI: 10.1021/jp311749z.

(2) Schreiner, P. R.; Wagner, J. P.; Reisenauer, H. P.; Gerbig, D.; Ley, D.; Sarka, J.; Császár, A. G.; Vaughn, A.; Allen, W. D. "Domino Tunneling," J. Am. Chem. Soc. 2015, 137, 7828-7834, DOI: 10.1021/jacs.5b03322.

InChIs

1: InChI=1S/C2H2O4/c3-1(4)2(5)6/h(H,3,4)(H,5,6)
InChIKey=MUBZPKHOEPUJKR-UHFFFAOYSA-N

Two interesting questions are addressed in a focal-point computational study of t-butyl radical and the t-butyl anion from the Schaefer group.¹ First, is the radical planar? EPR and PES studies from the 1970s indicate a pyramidal structure, with an inversion barrier of only 0.64 kcal mol^-1. The CCSD(T)/cc-pCVTZ optimized structure of t-butyl radical shows it to be pyramidal with the out-of-plane angle formed by one methyl group and the other three carbons of 22.9°, much less than the 54.7° of a perfect tetrahedron. Focal point analysis give the inversion barrier 0.74 kcal mol^-1, in outstanding agreement with experiment.

Second, what is the electron affinity (EA) of the t-butyl radical? Schleyer raised the concern that the alkyl anions may be unbound, and suggested that the electron affinity of t-butyl radical was -9.6 kcal mol^-1; in other words, the anion is thermodynamically unstable. This focal-point study shows just how sensitive the EA is to computational method. The HF/CBS value of the EA is -39.59 kcal mol^-1 (unbound anion), but the MP2/CBS value is +41.57 kcal mol^-1 (bound anion!). The CCSD/aug-cc-pVQZ value is -8.92 while the CCSD(T)/aug-cc-pVQZ value is +4.79 kcal mol^-1. The estimated EA at CCSDT(Q)/CBS is -1.88 kcal mol^-1, and inclusion of correction terms (including ZPE and relativistic effect) gives a final estimate of the EA as -0.48 kcal mol^-1, or a very weakly unbound t-butyl anion. It is somewhat disconcerting that such high-level computations are truly needed for some relatively simple questions about small molecules.

References

(1) Sokolov, A. Y.; Mittal, S.; Simmonett, A. C.; Schaefer, H. F. "Characterization of the t-Butyl Radical and Its Elusive Anion," J. Chem. Theory Comput. 2012, 8, 4323-4329, DOI: 10.1021/ct300753d.

Another remarkable piece of science from the Schreiner and Allen groups has appeared demonstrating the critical importance of combining experiment with computations.¹ (This one will surely be in the running for computational chemistry paper of the year.) Once again they examine tunneling from a carbene intermediate, but this time with an amazing conclusion that will have impact on chemistry textbooks!

Schreiner and Allen have previously examined a number of hydroxycarbenes (see these posts: A, B, C) and have found tunneling to be the main exit channel from these carbenes. The tunneling passes through barriers that are as large as 30 kcal mol^-1, and as expected, the deuterium labeled analogues have tunneling half lives that are exceptionally long, like 4000 years.

Now they examine methylhydroxycarbene 1,¹ which is interesting because there are two possible exit channels, leading to acetaldehyde 2 or vinyl alcohol 3. Previous gas-phase pyrolysis of pyruvic acid suggested the intermediacy of 1, which rearranges to 2 much more rapidly than to 3. However, G1 computations predict the barrier to 3 is smaller than the barrier to 2,² which should mean that 2 is the kinetic product!

Methylhydroxycarbene 1 was prepared by flash pyrolysis of pyruvic acid with capture of the products in an argon matrix. The carbene 1 was characterized by IR. The predicted frequencies (CCSD(T)/cc-pCVTZ – with corrections for anharmonicity) of 9 of the 11 bands of 1 are within 8 cm^-1 of the experimental frequencies. The OH and OD stretches, the ones not in agreement, are likely to be perturbed by the matrix. The predicted (MRCC/aug-cc-pVTZ) and experimental UV spectrum are also in close agreement.

Holding the matrix at 11 K and following the spectra of 1-3 led to the following important kinetic results: the half-life for formation of 2 is 66 min with no 3 observed to form. In addition, the rate for the deuterium labeled carbene to form 2 was too long for measuring, but was 196 minutes in Kr and 251 minutes in Xe. CCSD(T)/cc-pCVCZ computations followed by focal point methods gives the barrier to form acetaldehyde from 1 as 28.0 kcal mol^-1 while that to form vinyl alcohol 3 is much lower: 22.6 kcal mol^-1. (The structures of these three molecules and the transition states connecting them are shown in Figure 1.) Apparently, the reaction passes through or over the higher barrier in large preference over passing through or over the lower barrier!

1
TS12	2
TS13	3

Figure 1. CCSD(T)/cc-pCVTZ optimizes structures of 1-3 and the transition states connecting 1 to 2 and 1 to 3.

Precise mapping of the intrinsic reaction path at CCSD(T)/cc-pCVTZ allows for computing the WKB tunneling probabilities. This leads to the prediction of the half-life for the reaction 1 → 2 as 71 minutes, in excellent agreement with experiment. The computed half-life for the deuterium labeled reaction of 400 years and the computed half-life for 1 → 3 of 190 days are both in fine agreement with experiment.

Why does the reaction preferentially tunnel through the higher barrier? Well, the tunneling rate is dependent on the square root of the barrier height and linearly on the barrier width. The width is much smaller for the rearrangement to 2. The hydrogen needs to move a shorter amount in proceeding from 1to 2 than to 3, and in the rearrangement to vinyl alcohol a second hydrogen must migrate downwards to form the planar vinyl group. Basically, width beats out the height.

The important conclusion from this paper is the following: in addition to reactions being under kinetic or thermodynamic control, we must now consider a third options – a reaction under tunneling control!

A nice perspective on this paper and its implications has been written by Carpenter, who points out how this adds to our general notion of significant limitations to transition state theory.³

References

(1) Schreiner, P. R.; Reisenauer, H. P.; Ley, D.; Gerbig, D.; Wu, C.-H.; Allen, W. D., "Methylhydroxycarbene: Tunneling Control of a Chemical Reaction," Science, 2011, 332, 1300-1303, DOI: 10.1126/science.1203761.

(2) Smith, B. J.; Nguyen Minh, T.; Bouma, W. J.; Radom, L., "Unimolecular rearrangements connecting hydroxyethylidene (CH₃-C-OH), acetaldehyde (CH₃-CH:O), and vinyl alcohol (CH₂:CH-OH)," J. Am. Chem. Soc., 1991, 113, 6452-6458, DOI: 10.1021/ja00017a015

(3) Carpenter, B. K., “Taking the High Road and Getting There Before You,” Science, 2011, 332, 1269-1270, DOI: 10.1126/science.1206693.

InChIs

1: InChI=1/C2H4O/c1-2-3/h3H,1H3
InChIKey=JVKQHDUTAFISFX-UHFFFAOYAN

2: InChI=1/C2H4O/c1-2-3/h2H,1H3
InChIKey=IKHGUXGNUITLKF-UHFFFAOYAB

3: InChI=1/C2H4O/c1-2-3/h2-3H,1H2
InChIKey=IMROMDMJAWUWLK-UHFFFAOYAT

Schaefer, Csaszar, and Allen have applied the focal point method towards predicting the energies and structures of cysteine.¹ This very high level method refines the structures that can be used to compare against those observed by Alonso² in his laser ablation molecular beam Fourier transform microwave spectroscopy experiment (see this post). They performed a broad conformation search, initially examining some 66,664 structures. These reduced to 71 unique conformations at MP2/cc-pvTZ. The lowest 11 energy structures were further optimized at MP2(FC)/aug-cc-pV(T+d)Z. The four lowest energy conformations are shown in Figure 1 along with their relative energies.

I (0.0)	II (4.79)
III (5.81)	IV (5.95)

Figure 1. MP2(FC)/aug-cc-pV(T+d)Z optimized geometries and focal point relative energies (kJ mol^-1) of the four lowest energy conformers of cysteine.¹

The three lowest energy structures found here match up with the lowest two structures found by Alonso and the energy differences are also quite comparable: 4.79 kJ and 5.81 mol^-1 with the focal point method 3.89 and 5.38 kJ mol^-1 with MP4/6-311++G(d,p)// MP2/6-311++G(d,p). So the identification of the cysteine conformers made by Alonso remains on firm ground.

References

(1) Wilke, J. J.; Lind, M. C.; Schaefer, H. F.; Csaszar, A. G.; Allen, W. D., "Conformers of Gaseous Cysteine," J. Chem. Theory Comput. 2009, DOI: 10.1021/ct900005c.

(2) Sanz, M. E.; Blanco, S.; López, J. C.; Alonso, J. L., "Rotational Probes of Six Conformers of Neutral Cysteine," Angew. Chem. Int. Ed. 2008, 4, 6216-6220, DOI: 10.1002/anie.200801337

InChIs

Cysteine:
InChI=1/C3H7NO2S/c4-2(1-7)3(5)6/h2,7H,1,4H2,(H,5,6)/t2-/m0/s1
InChIKey: XUJNEKJLAYXESH-REOHCLBHBU

Malonaldehyde 1 possesses a very short intramolecular hydrogen bond. Its potential energy surface has two local minima (the two mirror image hydrogen-bonded structures) separated by a C_2v transition state. Schaefer reports a high-level computational study for the search for even shorter hydrogen bonds that might even lead to a single well on the PES.¹

The hydrogen bond distance is characterized by the non-bonding separation between the two oxygen atoms. Table 1 shows the O^…O distance for a number of substituted malonaldehydes computed at B3LYP/DZP++. Electron withdrawing groups on C₂ reduce the O^..O distance (see trend in 1 → 4). Electron donating groups on C₁ and C₃ also reduce this distance (see 5 and 6). Bulky substituents on the terminal carbons also reduce the O^…O distance (see 7). Combining all of these substituent effects in 8 leads to the very short O^…O distance of 2.380 Å.

Table 1. Distance (Å) between the two oxygen atoms and the barrier for hydrogen transfer of substituted malonaldehydes .¹

^aFocal point energy. ^bFocal point energy and corrected for zero-point vibrational energy.

A shorter O^…O distance might imply a smaller barrier for hydrogen transfer between the two oxygens. The structures of 8 and the transition state for its hydrogen transfer are shown in Figure 1. The energies of a number of substituted malonaldehydes were computed using the focal point method, and the barriers for hydrogen transfer are listed in Table 1. There is a nice correlation between the O^…O distance and the barrier height. The barrier for 8 is quite small, suggesting that with some bulkier substituents, the barrier might vanish altogether, leaving only a symmetric structure. In fact, the barrier appears to vanish when zero-point vibrational energies are included.

8

8TS

Figure 1. B3LYP/DZP++ optimized geometries of 8 and the transition state for hydrogen transfer 8TS.¹

References

(1) Hargis, J. C.; Evangelista, F. A.; Ingels, J. B.; Schaefer, H. F., "Short Intramolecular Hydrogen Bonds: Derivatives of Malonaldehyde with Symmetrical Substituents," J. Am. Chem. Soc., 2008, 130, 17471-17478, DOI: 10.1021/ja8060672.

InChIs

1: InChI=1/C3H4O2/c4-2-1-3-5/h1-4H/b2-1-
InChIKey=GMSHJLUJOABYOM-UPHRSURJBI

2: InChI=1/C4H3NO2/c5-1-4(2-6)3-7/h2-3,6H/b4-2-
InChIKey=BHYIQMFSOGUTRT-RQOWECAXBC

3: InChI=1/C3H3NO4/c5-1-3(2-6)4(7)8/h1-2,5H/b3-1+
InChIKey=JBBHDCMVSJADCE-HNQUOIGGBS

4: InChI=1/C3H5BO2/c4-3(1-5)2-6/h1-2,5H,4H2/b3-1+
InChIKey=IQNKNZSFMBIPBI-HNQUOIGGBX

5: InChI=1/C3H6N2O2/c4-2(6)1-3(5)7/h1,6H,4H2,(H2,5,7)/b2-1-/f/h5H2
InChIKey=AOZIOAJNRYLOAH-KRHGAQEYDI

6: InChI=1/C5H8O4/c1-8-4(6)3-5(7)9-2/h3,6H,1-2H3/b4-3+
InChIKey=BYYYYPBUMVENKB-ONEGZZNKBI

7: InChI=1/C11H20O2/c1-10(2,3)8(12)7-9(13)11(4,5)6/h7,12H,1-6H3/b8-7-
InChIKey=SOZFXLUMSLXZFW-FPLPWBNLBX

8: InChI=1/C3H5N3O4/c4-2(7)1(3(5)8)6(9)10/h7H,4H2,(H2,5,8)/b2-1+/f/h5H2
InChIKey=IHYUFGCOUITNJP-CHFMFTGODK

Schaefer and Allen have applied their focal point method to the question of the benzylic effect in the S_N2 reaction.¹ S_N2 reactions are accelerated when the attack occurs at the benzylic carbon, a well-known phenomenon yet the reason for this remains unclear. The standard textbook-like argument has been that the negative charge built up in the S_N2 transition state can be delocalized into the phenyl ring. However, solution phase Hammett studies are often U-shaped, indicating that both electron donating and withdrawing group accelerate the substitution reaction. (This is usually argued as indicative of a mechanism change from S_N2 to S_N1.)

The focal point method involves a series of very large computations where both basis set size and degree of electron correlation are systematically increased, allowing for an extrapolation to essentially infinite basis set and complete correlation energy. The energy of the transition state (relative to separated reactants) for four simple S_N2 reactions evaluated with the focal point method are listed in Table 1. The barrier for the benzylic substitutions is lower than for the methyl cases, indicative of the benzylic effect.

Table 1. Energy (kcal mol^-1) of the transition state relative to reactants.¹

To answer the question of why the benzylic substitution reactions are faster, they examined the charge distribution evaluated at B3LYP/DZP++. As seen in Table 1, this method does not accurately reproduce the activation barriers, but the errors are not terrible, and the trends are correct.

In Figure 1 are the geometries of the transition states for the reaction of fluoride with methylflouride or benzylfluoride. The NBO atomic charges show that the phenyl ring acquired very little negative charge at the transition state. Rather, the electric potential at the carbon under attack is much more revealing. The potential is significantly more positive for the benzylic carbon than the methyl carbon in both the reactant and transition states.

VC = -405.156 V	VC = -404.379 V

Figure 1. MP2/DZP++ transition states for the reaction of fluoride with methylfluoride and benzylflouride. NBO charges on F and C and the electrostatic potential in Volts.¹

They next examined the reaction of fluoride with a series of para-substituted benzylfluorides. The relation between the Hammet σ constants and the activation energy is fair (r = 0.971). But the relation between the electrostatic potential at the benzylic carbon (in either the reactant or transition state) with the activation energy is excellent (r = 0.994 or 0.998). Thus, they argue that it is the increased electrostatic potential at the benzylic carbon that accounts for the increased rate of the S_N2 reaction.

References

(1) Galabov, B.; Nikolova, V.; Wilke, J. J.; Schaefer III, H. F.; Allen, W. D., "Origin of the S_N2 Benzylic Effect," J. Am. Chem. Soc., 2008, 130, 9887-9896, DOI: 10.1021/ja802246y.

The very simple carbene hydroxymethylene, HOCH, has finally been prepared and characterized.¹ Glyoxylic acid CHOCO₂H is subjected to high-vacuum laser photolysis. It fragments into HOCH, which is then trapped into an argon matrix. The experimental IR frequencies match up very well with the CCSD(T)/cc-pVQZ harmonic frequencies of the trans isomer 1t that are also adjusted for anharmonic effects. The computed vertical excitation energy of 415 nm matches well with the experimental value of the maximum absorption in the UV/vis spectra of 427 nm.

The other very interesting experimental result is that HOCH has a lifetime of about 2 hours in the matrix, while the deuterated species DOCH is stable. To explain these results, Schreiner, Allen and co-workers optimized a number of structures on the PES at CCSD(T)/cc-pVQZ and computed their energies using the focal point technique. The optimized structures and their relative energies are given in Figure 1.

1t (0.0)	TS2 (29.7)	2 (-52.1)
TS1(26.8)
1c (4.4)

Figure 1. Optimized CCSD(T)/cc-pVQZ structures of HOCH isomers and their Focal Point relative energies (kcal mol^-1).¹

The barriers for rearrangement from 1t are both very high. Rearrangement to formaldehyde 2 requires crossing a barrier of 29.7 kcal mol^-1, while the barrier to convert to the cis isomer 1c is 26.8 kcal mol^-1. (Note that from 1c a cleavage into CO and H2 can occur, but this barrier is another 47.0 kcal mol^-1.) These barriers are too large to be crossed at the very low temperatures of the matrices. However, using the intrinsic reaction potential at CCSD(T)/cc-pVQZ and WKB theory, the tunneling lifetime of HOCH is computed to be 122 minutes, in excellent accord with the experiment. The lifetime for DOCH is computed to be over 1200 years. Thus, the degradation of hydroxymethylene is entirely due to tunneling through a very large classical barrier! This rapid tunneling casts serious doubt on the ability to ever identify any hydroxymethylene in interstellar space.

References

(1) Schreiner, P. R.; Reisenauer, H. P.; Pickard IV, F. C.; Simmonett, A. C.; Allen, W.
D.; Matyus, E.; Csaszar, A. G., "Capture of hydroxymethylene and its fast disappearance through tunnelling," Nature, 2008, 453, 906-909, DOI: 10.1038/nature07010.

InChI

1: InChI=1/CH2O/c1-2/h1-2H
2: InChI=1/CH2O/c1-2/h1H2