At the recent ACS meeting in New Orleans, Ken Houk spoke at the Dreyfus award session in honor of Michele Parrinello. Ken’s talk included discussion of some recent molecular dynamics studies of pericyclic reactions. Because of their similarities in approaches and observations, I will discuss three recent papers from his group (which Ken discussed in New Orleans) in this post.

The Cope rearrangement, a fundamental organic reaction, has been studied extensively by computational means (see Chapter 4.2 of my book). Mackey, Yang, and Houk examine the degenerate Cope rearrangement of 1,5-hexadiene with molecular dynamics at the (U)B3LYP/6-31G(d) level.¹ They examined 230 trajectories, and find that of the 95% of them that are reactive, 94% are trajectories that directly cross through the transition zone. By this, Houk means that the time gap between the breaking and forming C-C bonds is less than 60 fs, the time for one C-C bond vibration. The average time in the transition zone is 35 fs. This can be thought of as “dynamically concerted”. For the other few trajectories, a transient diradical with lifetime of about 100 fs is found.

The dimerization of cyclopentadiene finds the two [4+2] pathways merging into a single bispericylic transition state. ² Only a small minority (13%) of the trajectories sample the region about the Cope rearrangement that interconverts the two mirror image dimers. These trajectories average about 60 fs in this space, which comes from the time separation between the formation of the two new C-C bonds. The majority of the trajectories quickly pass through the dimerization transition zone in about 18 fs, and avoid the Cope TS region entirely. These paths can be thought of as “dynamically concerted”, while the other set of trajectories are “dynamically stepwise”. It should be noted however that the value of S² in the Cope transition zone are zero and so no radicals are being formed.

Finally, Yang, Dong, Yu, Yu, Li, Jamieson, and Houk examined 15 different reactions that involve ambimodal (i.e. bispericyclic) transition states.³ They find a strong correlation between the differences in the bond lengths of the two possible new bond vs. their product distribution. So for example, in the reaction shown in Scheme 1, bond a is the one farthest along to forming. Bond b is slightly shorter than bond c. Which of these two is formed next is dependent on the dynamics, and it turns out the P_ab is formed from 73% of the trajectories while P_ac is formed only 23% of the time. This trend is seen across the 15 reaction, namely the shorter of bond b or c in the transition state leads to the larger product formation. When competing reactions involve bonds with differing elements, then a correlation can be found with bond order instead of with bond length.

Scheme 1

References

1) Mackey, J. L.; Yang, Z.; Houk, K. N., "Dynamically concerted and stepwise trajectories of the Cope rearrangement of 1,5-hexadiene." Chem. Phys. Lett. 2017, 683, 253-257, DOI: 10.1016/j.cplett.2017.03.011.

2) Yang, Z.; Zou, L.; Yu, Y.; Liu, F.; Dong, X.; Houk, K. N., "Molecular dynamics of the two-stage mechanism of cyclopentadiene dimerization: concerted or stepwise?" Chem. Phys. 2018, in press, DOI: 10.1016/j.chemphys.2018.02.020.

3) Yang, Z.; Dong, X.; Yu, Y.; Yu, P.; Li, Y.; Jamieson, C.; Houk, K. N., "Relationships between Product Ratios in Ambimodal Pericyclic Reactions and Bond Lengths in Transition Structures." J. Am. Chem. Soc. 2018, 140, 3061-3067, DOI: 10.1021/jacs.7b13562.

Bispericyclic reactions occur when two different pericyclic reactions merge to have a single transition state. An example of this is the joining of two [3,3]-sigmatopic rearrangements of 1 that merge to have a single transition state. Lopez, Faza, and Lopez have examined the dynamics of this reaction.¹

Because of the symmetry of the species along this reaction pathway, the products of the two different rearrangements are identical, and will be formed in equal amounts, though they are produced from a single transition state with the reaction pathway bifurcating due to a valley-ridge inflection post TS.

The interesting twist that is explored here is when 1 is substituted in order to break the symmetry. The authors have examined 3x with either fluorine, chlorine, or bromine. The critical points on the reactions surface were optimized at M06-2X/Def2TZVPP. In all three cases a single bispericyclic transition state 3TS1x is found, which leads to products 4a and 4b. A second transition state 4TSx corresponds to the [3,3]-rearrangement that interconverts the two products. The structures of 1TS, 3TS1F, and 3TS1Cl are shown in Figure 1.

1TS

3TS1F

3TS1Cl

Figure 1. M06-2X/Def2TZVPP optimized geometries of 1TS, 3TS1F, and 3TS1Cl.

The halogen substitution breaks the symmetry of the reaction path. This leads to a number of important changes. First, the C₄-C₅ and C₇-C₈ distances, which are identical in 1TS, are different in the halogen cases. Interestingly, the distortions are dependent on the halogen: in 3TS1F C₄-C₅ is 0.2 Å longer than C₇-C₈, but in 3TS1Cl C₇-C₈ is much longer (by 0.65 Å) than C₄-C₅. Second, the products are no longer equivalent with the halogen substitution. Again, this is halogen dependent: 4bF is 4.0 kcal mol^-1 lower in energy than 4aF, while 4aCl is 8.2 kcal mol^-1 lower than 4bCl.

These difference manifest in very different reaction dynamics. With trajectories initiated at the first (bispericyclic) transiting state, 89% end at 4bF and 9% end at 4aF, a ratio far from unity that might be expected from both products resulting from passage through the same TS. The situation is even more extreme for the chlorine case, where all 200 trajectories end in 4aCl. This is yet another example of the role that dynamics play in reaction outcomes (see these many previous posts).

References

1) Villar López, R.; Faza, O. N.; Silva López, C., "Dynamic Effects Responsible for High Selectivity in a [3,3] Sigmatropic Rearrangement Featuring a Bispericyclic Transition State." J. Org. Chem. 2017, 82 (9), 4758-4765, DOI: 10.1021/acs.joc.7b00425.

InChIs

1: InChI=1S/C9H12/c1-3-9-6-4-8(2)5-7-9/h1-2,4-7H2
InChIKey=RRXCPJIEZVQPSZ-UHFFFAOYSA-N

2: InChIInChIKey=AMBNQWVPTPHADI-UHFFFAOYSA-N

3F: InChI=1S/C9H8F4/c1-3-7-5-4-6(2)8(10,11)9(7,12)13/h1-2,4-5H2
InChIKey=VZFAQFJKHDWJDN-UHFFFAOYSA-N

3Cl: InChI=1S/C9H8Cl4/c1-3-7-5-4-6(2)8(10,11)9(7,12)13/h1-2,4-5H2
InChIKey=AIVUHFMHIMNOJB-UHFFFAOYSA-N

4aF: InChI=1S/C9H8F4/c1-5-4-6(8(10)11)2-3-7(5)9(12)13/h1-4H2
InChIKey=NAUUHIHYMAOMIF-UHFFFAOYSA-N

4aCl: InChI=1S/C9H8Cl4/c1-5-4-6(8(10)11)2-3-7(5)9(12)13/h1-4H2
InChIKey=MMCKDJXQYSGQEH-UHFFFAOYSA-N

4bF: InChI=1S/C9H8F4/c1-5-4-6(2)8(10,11)9(12,13)7(5)3/h1-4H2
InChIKey=LMFNAIRCNARWSX-UHFFFAOYSA-N

4bCl: InChI=1S/C9H8Cl4/c1-5-4-6(2)8(10,11)9(12,13)7(5)3/h1-4H2
InChIKey=NOFFASDSCUGRTP-UHFFFAOYSA-N

Despite the fact that Wes Borden has indicated the he has written his last paper on the Cope rearrangement (see my interview with Wes at the end of Chapter 3), others remain intrigued by this reaction and continue to report on it. In a recent JACS communication, Tantillo¹ examines the palladium-promoted Cope rearrangement.

The ordinary Cope rearrangement displays chameleonic character – switching from concerted to stepwise with a diradical intermediate – based on substituents. The palladium-promoted Cope is suggested to proceed through a stepwise mechanism with a zwitterionic intermediate (Scheme 1).²

Scheme 1.

Tantillo¹ has examined a variety of these rearrangements at the B3LYP/LANL2DZ level. The palladium complex is PdCl₂NCMe. For all cases where R is a substituted phenyl group, the mechanism is stepwise, with the intermediate 1 sitting in a shallow well. The most stable intermediate (based on lying in the deepest well) is with the 4-dimethylaminophenyl group, and the well is 5.1 kcal mol^-1 deep. The structures of the transition state (2-pNMe₂) and the intermediate (1-pNMe₂) are shown in Figure 1.

2-pNMe2

1-pNMe2

Figure 1. B3LYP/LANL2DZ optimized structures of 2-pNMe₂ and 1-pNMe₂.¹

However, the well associated with 1 can be very shallow, as little as 0.4 kcal mol^-1 (R = 4-trifluoroimethylphenyl and 4-nitrophenyl). This suggests that perhaps when properly substituted the intermediate might vanish and the reaction become concerted. This is in fact what happens when R is CF₃, CN, or H. The transition state for the reaction with R = H is shown in Figure 2. So, this metal-assisted Cope rearrangement displays chameleonic behavior, just like the metal-free case, except that the intermediate is zwitterionic with the metal, instead of diradical in the metal-free cases.

2-H

Figure 1. B3LYP/LANL2DZ optimized structure of 2-H.¹

References

(1) Siebert, M. R.; Tantillo, D. J., "Transition-State Complexation in Palladium-Promoted [3,3] Sigmatropic Shifts," J. Am. Chem. Soc. 2007, 129, 8686-8687, DOI: 10.1021/ja072159i.

(2) Overman, L. E.; Renaldo, A. E., "Catalyzed Sigmatropic Rearrangements. 10. Mechanism of the Palladium Dichloride Catalyzed Cope Rearrangement of Acyclic Dienes. A Substituent Effect Study," J. Am. Chem. Soc. 1990, 112, 3945-3949, DOI: 10.1021/ja00166a034.

Here as an interesting, relatively straightforward example of how modern computational methods can help elucidate a reaction mechanism. Brinker¹ examined the thermolysis of (1S,2R,5R,7S,8R)-4,5-dibromotricyclo[6.2.1.0^2,7]undeca-3,9-diene 1. The observed products were cyclopentadiene (and its dimer), bromobenzene and (1R,2S,6S,7R,10R)-1,10-dibromotricyclo[5.2.2.0^2,6]undeca-3,8-diene
2. They proposed two possible mechanisms to account for these products. In the first mechanism, 1 can convert to 2 via a Cope rearrangement (path a, Scheme 1). The alternative mechanism has 1 undergo a retro-Diels-Alder reaction to produce 1,6-dibromo-1,3-cyclohexadiene 3 and cyclopentadiene 4 (path b, Scheme 1) 3 can then lose HBR to give bromobenzene. But more interesting is the possibility that cyclopentadiene and 3 can undergo a Diels-Alder reaction (path c, Scheme 1), but one with role reversal, i.e. cylopentadiene acts as the dienophile here, rather than the diene component as in the reverse of path b. This second Diels-Alder reaction (path c) produces 2.

Scheme 1

Brinker optimized the structures in Scheme 1, along with the transition states from paths a-c, at B3LYP/6-31G(d). These structures are shown in Figure 1 and their relative energies are listed in Table 1. The Cope rearrangement is favored over the retro-Diels-Alder by 3.6 kcal mol^-1. While the subsequent Diels-Alder step (path c) has a low electronic barrier (21.7 kcal mol^-1), it is enthalpically disfavored and the free energy barrier is high (40.4 kcal mol^-1. Thus, formation of 2 derives mostly from the direct Cope rearrangement of 2. Production of bromobenzene from 2 results from the retro-Diels-Alder (path b) followed by loss of HBr.

Table 1. Electronic and Free Energies (kcal mol^-1­) computed at B3LYP/6-31G(d).¹

1 xyz file	2 xyz files
TS(a) xyz files	TS(b) xyz file
TS(c) xyz file

Figure 1. B3LYP/6-31G(d) optimized structures.¹

InChI:

1: InChI=1/C11H12Br2/c12-10-4-8-6-1-2-7(3-6)9(8)5-11(10)13/h1-2,4,6-9,11H,3,5H2/t6-,7+,8-,9+,11-/m1/s1

2: InChI=1/C11H12Br2/c12-10-6-7-4-5-11(10,13)9-3-1-2-8(7)9/h1,3-5,7-10H,2,6H2/t7-,8+,9+,10+,11+/m0/s1

References

(1) Su, K. J.; Mieusset, J. L.; Arion, V. B.; Brecker, L.; Brinker, U. H., “Cope Rearrangement versus a Novel Tandem Retro-Diels-Alder-Diels-Alder Reaction with Role reversal,” Org. Lett. 2007, 9, 113-115, DOI: 10.1021/ol0626793

A Stable Bis-allyl Intermediate on the Cope PES

As discussed in Chapter 3.2, the prototypical Cope rearrangement (the degenerate rearrangement of 1,5-hexadiene 1) is understood to proceed through a single concerted transition state. The concerted transition state 2 is described by three resonance structures (Scheme 1), and this allows for understanding the chameleonic nature of the substituted Cope rearrangement. For example, radical stabilizing groups at the 2 and 5 positions would favor the cyclohexyl-diyl structure.

Scheme 1

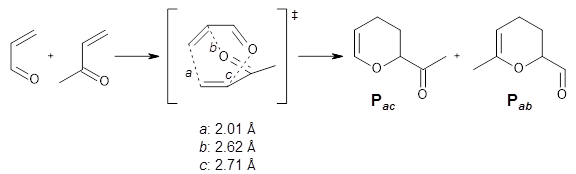
Schreiner computed the reaction path at BD(T)/cc-pVDZ//BLYP/6-31G* for 64 different variations of the Cope rearrangement.¹ A representative sampling from these is presented in Figure 1. The Cope rearrangements are found to fall into one of three categories. The first, called type 1, are concerted rearrangements. Type 2 rearrangements have two competing pathways: either through a concerted transition state or a diradical intermediate. The last group, type 3, comprises nonconcerted reactions with a cyclohexyl-diyl intermediate. Schreiner generalizes the results to the following rule: a nonconcerted reaction takes place when biradical intermediates are stabilized either by allyl or aromatic resonance.

Figure 1. Examples of the three type of Cope rearrangements. Relative energies, in kcal mol-1, were computed at BD(T)/cc-pVDZ//BLYP/6-31G*.1

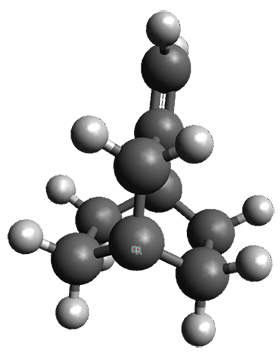
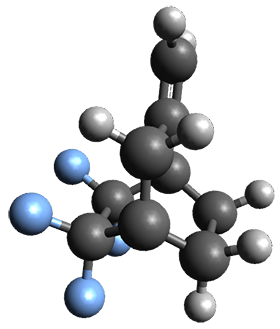
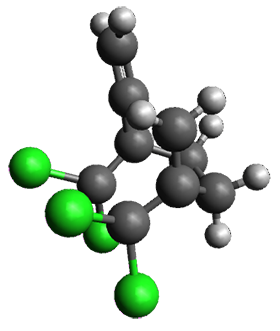
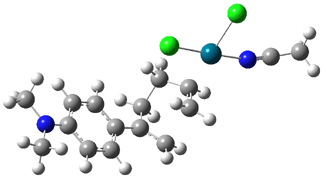
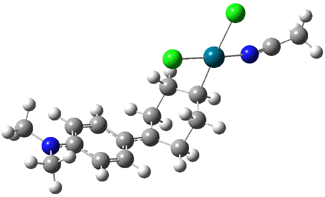
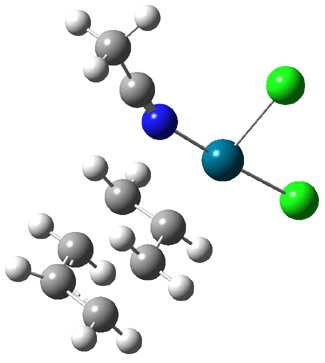
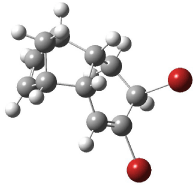
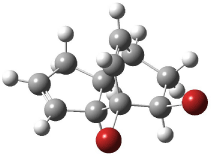
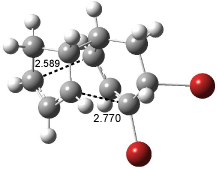
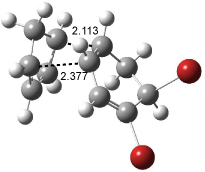
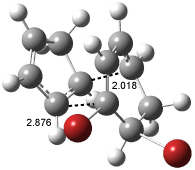
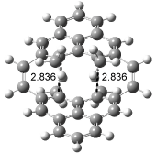
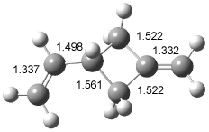
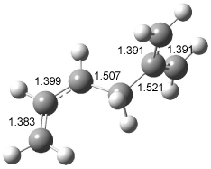
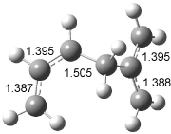
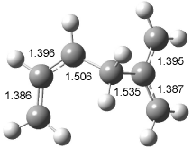
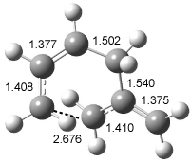
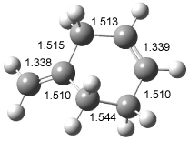
Interestingly, Schreiner’s study identified reactions where the diyl is a stable intermediate, but he identified no case where the other extreme – two allyl radicals – appeared as a stable intermediate. Kertesz, in 2006, discovered just such an example with the Cope rearrangement of 3.² Using B3LYP and BPW91 computations with two different basis sets, he identified the stable diradical 5. This structure, shown in Figure 2, clearly has very long distances – 2.836 Å – separating the ends of the two “allylic” components. A true transition state 4 connects the reactant 3 with the intermediate 5 (see Figure 2). The activation energy is 6.3 kcal mol^-1 and the intermediate 5 lies 3.3 kcal mol^-1 above 3.

3	4	5
xyz file	xyz file	xyz file
Figure 2. B3LYP/6-31G(d) optimized structures of 3-5. Distances (Å) shown are between C1-C6 and C3-C4 of the hexadiene component of the Cope rearrangement.2

Why does a stable bis-allyl analogue exist on the Cope reaction surface of 3? In the prototype Diels-Alder reaction of 1,5-hexadiene, the possible bis-allyl intermediate (i.e., two isolated allyl radicals) is about 26 kcal mol^-1 higher in energy than the Cope transition state. Only with significant radical stabilization might one expect a bis-allyl intermediate to occur. One can consider 5 as composed of two bridged phenalenyl radicals (6). Phenalenyl radical is stable due to electron delocalization; its ESR spectrum has been observed, but it has not been isolated, instead dimerizing to give 7.³ In addition to the stabilization afforded by the extensive delocalization of the radical within the phenalenyl system, two phenalenyl systems can also interact through overlap of their π-systems, creating what has been termed π-dimerization.^4-6 MRMP2 computations suggest that the π-dimerization energy of 6 is 11 kcal mol^-1.⁷ While the geometry of 5 is not ideal for π-dimerization, its structure clearly indicates some stacking of the two phenalenyl fragments. Both the enhanced electron delocalization about the large phenalenyl system along with π-dimerization provides sufficient stabilization that the bis-allyl intermediate exits on the Cope rearrangement pathway. This now completes all of the options for how the Cope rearrangement may occur: either directly through a concerted transition state, or multi-step process with a 1,6-diyl intermediate or a bis-allyl intermediate.

Cope Rearrangement of 3-Vinylmethylenecyclobutane

3-Vinylmethylenecyclobutane 8 can undergo a myriad of thermal rearrangements involving [1,3]- and [3,3]-shifts.⁸ The Cope rearrangement of 8 to 9 has a barrier of 35.7 kcal mol^-1.⁹ This large barrier is consistent with cleavage of a C-C bond leading to a diradical intermediate.

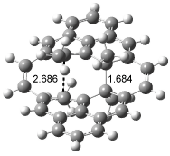
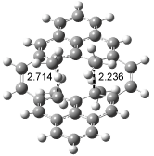
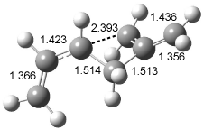
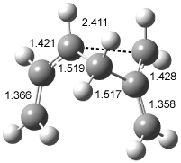
Houk has recently confirmed the diradical nature of this rearrangement.¹⁰ The geometries of all reactants intermediates, products and transition states were optimized at UB3LYP/6-31+G(d) and single-point energies were evaluated at CASPT2(6,6)/6-31G(d). Two diradical intermediates, 10 and 11, lie 30.0 and 32.0 kcal mol^-1, respectively, above 8. These intermediates are separated by a small barrier, 1.5 kcal mol^-1 from 10, and a barrier of 2.0 kcal mol^-1 interconverts mirror versions of 10. All of these paths are sketched in Scheme 3 and the geometries of the critical points are displayed in Figure 3.

Scheme 3

8 xyz file
TS8-10 xyz file	TS8-11 xyz file
10 xyz file	TS10-11 xyz file	11 xyz file
TS11-9x xyz file	TS11-9n xyz file
9 xyz file

Figure 3. Optimized Structures of the critical points in Scheme 3.¹⁰

Only the reaction going forward from 11 can lead to product 9. There are two such routes, involving an exo or endo approach. They are of similar energy, and also very close in energy to that of the diradical intermediates. Houk concludes that the diradical intermediates “have substantial conformational freedom and very low barriers for forming stereo- and regioisomeric forms of the ring-enlarged product”, in agreement with the experimentally observed lack of any region- or stereoselectivity in the thermal reactions of 8. The computed barrier, 34.9 kcal mol^-1 for TS8-10, is in good accord with the experimental barrier of 35.7 kcal mol^-1.

A study by Jung¹¹ the year before actually inspired Houk’s work. Jung discovered that appropriately substituted vinylmethylcyclohexenes will undergo very selective Cope rearrangements; for example, thermolysis of 8a produces 9a in greater than 90% yield. This result is quite contrary to that normally observed for vinylmethylcyclohexene thermoylsis: many products with virtually complete scrambling of all stereochemical information.

Examination of the rearrangement of 8a is computationally prohibitive, so Houk looked at the effect of individual substituents. The role of the trialkylsiloxy group was evaluated through the rearrangement of 8b, leading to diradicals 10b and 11b (Scheme 4). The transition state leading to 11b is 1.5 kcal mol^-1 below that leading to 10b. This is opposite the relative ordering of the transition states in the parent reaction, indicating that siloxy substitution would favor the path that leads to direct Cope rearrangement, which must pass through 11. The preference for the opposite TS with the siloxy group results from its torquoselectivity (See Chapter 3.5) Since 11b is more stable than 10b, this would also help preserve the stereochemistry during the rearrangement.

Scheme 4

The effects of the terminal substituents were also evaluated. As shown in Scheme 5, the Cope rearrangement of 8b is predicted to proceed with distinct stereoselectivity. The ring opening step preferentially produces diradical intermediate 12 over 13. The ring forming step is also stereoselective: 12 cyclizes to 14 in a 3:1 ratio, while the ring closure of 13 predominantly gives 15. Overall, the rearrangement of 8b is predicted to give a product ratio 14:15 of 2:1. This is in accord with the Jung’s experimental observation.

Scheme 5

References

(1) Navarro-Vazquez, A.; Prall, M.; Schreiner, P. R., “Cope Reaction Families: To Be or Not to Be a Biradical,” Org. Lett. 2004, 6, 2981-2984, DOI: 10.1021/ol0488340

(2) Huang, J.; Kertesz, M., “Stepwise Cope Rearrangement of Cyclo-biphenalenyl via an Unusual Multicenter Covalent π-Bonded Intermediate,” J. Am. Chem. Soc. 2006, 128, 7277-7286, DOI: 10.1021/ja060427r

(3) Zheng, S.; Lan, J.; Khan, S. I.; Rubin, Y., “Synthesis, Characterization, and Coordination Chemistry of the 2-Azaphenalenyl Radical,” J. Am. Chem. Soc. 2003, 125, 5786-5791, DOI: 10.1021/ja029236o

(4) Goto, K.; Kubo, T.; Yamamoto, K.; Nakasuji, K.; Sato, K.; Shiomi, D.; Takui, T.; Kubota, M.; Kobayashi, T.; Yakusi, K.; Ouyang, J., “A Stable Neutral Hydrocarbon Radical: Synthesis, Crystal Structure, and Physical Properties of 2,5,8-Tri-tert-butyl-phenalenyl,” J. Am. Chem. Soc. 1999, 121, 1619-1620, DOI: 10.1021/ja9836242

(5) Suzuki, S.; Morita, Y.; Fukui, K.; Sato, K.; Shiomi, D.; Takui, T.; Nakasuji, K., “Aromaticity on the Pancake-Bonded Dimer of Neutral Phenalenyl Radical as Studied by MS and NMR Spectroscopies and NICS Analysis,” J. Am. Chem. Soc. 2006, 128, 2530-2531, DOI: 10.1021/ja058387z

(6) Takano, Y.; Taniguchi, T.; Isobe, H.; Kubo, T.; Morita, Y.; Yamamoto, K.; Nakasuji, K.; Takui, T.; Yamaguchi, K., “Hybrid Density Functional Theory Studies on the Magnetic Interactions and the Weak Covalent Bonding for the Phenalenyl Radical Dimeric Pair,” J. Am. Chem. Soc. 2002, 124, 11122-11130, DOI: 10.1021/ja0177197

(7) Small, D.; Zaitsev, V.; Jung, Y.; Rosokha, S. V.; Head-Gordon, M.; Kochi, J. K., “Intermolecular π-to-π Bonding between Stacked Aromatic Dyads. Experimental and Theoretical Binding Energies and Near-IR Optical Transitions for Phenalenyl Radical/Radical versus Radical/Cation Dimerizations,” J. Am. Chem. Soc. 2004, 126, 13850-13858, DOI: 10.1021/ja046770i

(8) Kozhushkov, S. I.; Kuznetsova, T. S.; Zefirov, N. S., “Mechanism of Thermal Isomerization of 3-Vinylmethylenecyclobutane into 4-Methylenecyclohexane,” Dokl. Akad. Nauk SSSR, 1988, 299, 1395-1399,

(9) Dolbier, W. R.; Mancini, G. J., “Non-concerted Thermal Reorganizations 3,3-Divinylmethylenecyclobutane,” Tetrahedron Lett. 1975, 16, 2141-2144, DOI: 10.1016/S0040-4039(00)72661-X.

(10) Zhao, Y. L.; Suhrada, C. P.; Jung, M. E.; Houk, K. N., “Theoretical Investigation of the Stereoselective Stepwise Cope Rearrangement of a 3-Vinylmethylenecyclobutane,” J. Am. Chem. Soc. 2006, 128, 11106-11113, DOI: 10.1021/ja060913e

(11) Jung, M. E.; Nishimura, N.; Novack, A. R., “Versatile Diastereoselectivity in Formal [3,3]-Sigmatropic Shifts of Substituted 1-Alkenyl-3-alkylidenecyclobutanols and Their Silyl Ethers,” J. Am. Chem. Soc. 2005, 127, 11206-11207, DOI: 10.1021/ja051663p

InChI

3: InChI=1/C34H26/c1-19-21-11-12-22-16-24-8-6-10-26-18-28-14-13-27-17-25-9-5-7-23(15-21)29(25)31(19)33(27,3)34(28,4)32(20(22)2)30(24)26/h5-18H,1-4H3/b12-11-/t33-,34+

5: InChI=1/C34H26/c1-19-23-11-12-25-17-29-9-6-10-30-18-26(22(4)32(21(25)3)34(29)30)14-13-24-16-28-8-5-7-27(15-23)33(28)31(19)20(24)2/h5-18H,1-4H3/b12-11-,14-13-

6: InChI=1/C13H9/c1-4-10-6-2-8-12-9-3-7-11(5-1)13(10)12/h1-9H

7: InChI=1/C26H18/c1-5-17-9-3-11-23-21(15-13-19(7-1)25(17)23)22-16-14-20-8-2-6-18-10-4-12-24(22)26(18)20/h1-16,21-22H

8: InChI=1/C7H10/c1-3-7-4-6(2)5-7/h3,7H,1-2,4-5H2

9: InChI=1/C7H10/c1-7-5-3-2-4-6-7/h2-3H,1,4-6H2