The concept of complementarity between enzyme and substrate, especially the transition state for reactions at the substrate, is a key element of Pauling’s model for enzymatic activity. Koshland’s “induced fit” modification suggests that the enzyme might change its structure during the binding process to either destabilize the reactant or help stabilize the TS. These concepts are now tested in a very nice model by Stoddart, Siegel and coworkers.¹

Stoddart recently reported the host compound ExBox⁴⁺ 1 and demonstrated that it binds planar polycyclic aromatic hydrocarbons.² (I subsequently reported DFT computations on this binding.) The twist in this new paper is the binding of corranulene 2 inside ExBox⁴⁺ 1. Corranulene is bowl-shaped, with a bowl inversion barrier of 11.5 kcal mol^-1 (10.92 kcal mol^-1 at B97D/Def2-TZVPP).

The corranulene bowl is too big to fit directly into 1 without some distortions. The x-ray structure of the complex of 1 with 2 inside shows the width of 1 expanding by 0.87 Å and the bowl depth of 2 decreasing by 0.03 Å. The B97D/Def2-TZVPP optimized geometry of this complex (shown in Figure 1) shows similar distortions – the width of 1 increases by 0.37 Å (gas) or 0.29 Å (acetone solution), while the bowl depth of 2 decreases by 0.03 Å (gas) or 0.02 Å (solution).

ground state

transition state

Figure 1. B97D/Def2-TZVPP optimized geometries of the complex of 2 inside 1 (a) ground state and (b) transition state.

The calculated structure of the bowl inversion transition state of 2 inside of 1 is shown in Figure 1. 2 is planar at the TS. The experimental inversion barrier (determined by variable temperature NMR line shift analysis) is 7.88 kcal mol^-1, while the calculated barrier is 8.77 kcal mol^-1. The reduction in the bowl inversion barrier of 2 inside of 1 is therefore about 2.5 kcal mol^-1. The authors argue that this barrier reduction can be attributed to about 0.5 kcal mol^-1 of destabilization of the ground state of 2 along with 2 kcal mol^-1 of stabilization of the transition state afforded by the host. This study thus confirms the notions of a host reducing a barrier (through both transition state stabilization and ground state destabilization) and induced fit.

References

(1) Juríček, M.; Strutt, N. L.; Barnes, J. C.; Butterfield, A. M.; Dale, E. J.; Baldridge, K. K.; Stoddart, J. F.; Siegel, J. S. "Induced-fit catalysis of corannulene bowl-to-bowl inversion," Nat. Chem. 2014, 6, 222-228, DOI: 10.1038/nchem.1842.

(2) Barnes, J. C.; Juríček, M.; Strutt, N. L.; Frasconi, M.; Sampath, S.; Giesener, M. A.; McGrier, P. L.; Bruns, C. J.; Stern, C. L.; Sarjeant, A. A.; Stoddart, J. F. "ExBox: A Polycyclic Aromatic Hydrocarbon Scavenger," J. Am. Chem. Soc. 2012, 135, 183-192, DOI: 10.1021/ja307360n.

(3) Bachrach, S. M. "DFT Study of the ExBox·Aromatic Hydrocarbon Host–Guest Complex," J. Phys. Chem. A 2013, 117, 8484-8491, DOI: 10.1021/jp406823t.

InChIs

1: InChI=1S/C48H40N4/c1-2-38-4-3-37(1)33-49-25-17-45(18-26-49)41-9-11-43(12-10-41)47-21-29-51(30-22-47)35-39-5-7-40(8-6-39)36-52-31-23-48(24-32-52)44-15-13-42(14-16-44)46-19-27-50(34-38)28-20-46/h1-32H,33-36H2/q+4
InChIKey=ZMELWAYDWQWNOQ-UHFFFAOYSA-N

2: InChI=1S/C20H10/c1-2-12-5-6-14-9-10-15-8-7-13-4-3-11(1)16-17(12)19(14)20(15)18(13)16/h1-10H
InChIKey=VXRUJZQPKRBJKH-UHFFFAOYSA-N

Annulenes can twist, and I have blogged about a number of examples (cations and neutrals). The twist can be portioned into a twist associated with the dihedral angle as one progresses around the compound and writhe which is associated with distortion of the annulene into a third dimension.¹

Herges has prepared the 36-annulene 1 where the anthracenyl units were introduced to force the loop out of plane.² Four different conformations of 1 where isolated by crystallization out of different solvents. 1a and 1b were produced in benzene, and they differ by having two half-twists (L_k=2) and one half-twist (L_k=1), respectively. 1c was isolated from DMF, with one half-twist. 1d was isolated from Et₂O/CH₂Cl₂.

Computations at the B3LYP/6-31g* level identified 10 low lying conformations, and the ones corresponding to the experimentally observed forms are shown in Figure 1. The computed conformer that matches with 1d differs form the experimental version by a rotation about one single bond, and the computed version has a different topology than the experiment. One item of note is that all of the 10 computed conformers are dominated by the twist (T_w) and have very small writhe.

1a	1b
1c	1d
1e

Figure 1. B3LYP/6-31G* optimized structures of 1a-e.

Though not isolated in experiment, one of the low lying conformers has three half-twists (L_k=3) and is also shown in Figure 1 as 1e. Identification of this highly twisted species would be quite interesting.

References

(1) Fowler, P. W.; Rzepa, H. S., "Aromaticity rules for cycles with arbitrary numbers of half-twists," Phys. Chem. Chem. Phys., 2006, 8, 1775-1777, DOI: 10.1039/b601655c.

(2) Mohebbi, A.; Mucke, E. K.; Schaller, G.; Köhler, F.; Sönnichsen, F.; Ernst, L.; Näther, C.; Herges, R., "Singly and Doubly Twisted [36]Annulenes: Synthesis and Calculations," Chem. Eur. J., 2010, 16, 7767-7772, DOI: 10.1002/chem.201000277,

InChIs

1: InChI=1/C80H52/c1-9-25-65-57(17-1)73-45-41-53-33-35-54(36-34-53)42-46-75-61-21-5-13-29-69(61)79(70-30-14-6-22-62(70)75)51-52-80-71-31-15-7-23-63(71)76(64-24-8-16-32-72(64)80)48-44-56-39-37-55(38-40-56)43-47-74-59-19-3-11-27-67(59)78(68-28-12-4-20-60(68)74)50-49-77(65)66-26-10-2-18-58(66)73/h1-52H/b45-41-,46-42+,47-43-,48-44+,50-49+,52-51-,53-41-,54-42-,55-43-,56-44-,73-45-,74-47-,75-46-,76-48-,77-49-,78-50+,79-51+,80-52+
InChIKey=KXWPWHPRFOXOIX-IFDMNBDGBZ

Since Heilbronner¹ proposed the Möbius annulene in 1964, organic chemists have been fascinated with this structure and many have tried to synthesize an example. I have written many blog posts (1, 2, 3, 4, 5) related to computed Möbius compounds. Now, Herges and Grimme and co-workers have looked at cationic Möbius annulenes.

For the [9]annulene cation,² a variety of DFT methods, along with SCS-MP2 and CCSSD(T) computations suggest that the lowest energy Hückel (1h) and Möbius (1m) structures, shown in Figure 1, are very close in energy. In fact, the best estimate (CCSD(T)/CBS) is that they differ by only 0.04 kcal mol^-1. Laser flash photolysis of 9-chlorobicyclo[6.1.0]nona-2,4,6-triene suggest however that only the Hückel structure is formed, and that its short lifetime is due to rapid electrocyclic ring closure.

In a follow-up study, Herges has examined the larger annulene cations, specifically [13]-, [17]- and [21]-annulenes. ³ The Möbius form of [13]-annulene cation (2m) is predicted to be 11.0 kcal mol^-1 lower in energy that the Hückel (2h) form at B3LYP/6-311+G**. The structures of these two cations are shown in Figure 1. The Möbius cation 2m is likely aromatic, having NICS(0)= -8.95. Electrocyclic ring closure of 2m requires passing through a barrier of at least 20 kcal mol^-1, suggesting that 2m is a realistic target for preparation and characterization.

1h	1m
2h	2m

Figure 1. Optimized structures of 1 (CCSD(T)/cc-pVTZ)² and 2 (B3LYP/6-311+G**)³.

The energy difference between the Möbius and Hückel structures of the larger annulenes is very dependent on computational method, but in all cases the difference is small. Thus, Herges concludes that [13]-annulene cation should be the sole target of synthetic effort toward identification of a Möbius annulene. Experimental studies are eagerly awaited!

References

(1) Heilbronner, E., “Huckel molecular orbitals of Mobius-type conformations of annulenes,” Tetrahedron Lett., 1964, 5, 1923-1928, DOI: 10.1016/S0040-4039(01)89474-0.

2) Bucher, G.; Grimme, S.; Huenerbein, R.; Auer, A. A.; Mucke, E.; Köhler, F.; Siegwarth, J.; Herges, R., "Is the [9]Annulene Cation a Möbius Annulene?," Angew. Chem. Int. Ed., 2009, 48, 9971-9974, DOI: http://dx.doi.org/10.1002/anie.200900886

(3) Mucke, E.-K.; Kohler, F.; Herges, R., "The [13]Annulene Cation Is a Stable Mobius Annulene Cation," Org. Lett., 2010, 12, 1708–1711, DOI: 10.1021/ol1002384

InChIs

1: InChI=1/C9H9/c1-2-4-6-8-9-7-5-3-1/h1-9H/q+1/b2-1-,5-3-,6-4-,9-7-
InChIKey=LIUDWUIEJKKGNI-BWYSQNKRBF

2: InChI=1/C13H13/c1-2-4-6-8-10-12-13-11-9-7-5-3-1/h1-13H/q+1/b2-1-,5-3-,6-4-,9-7-,10-8-,13-11-
InChIKey=FUBPZYTZTJGXKZ-OGBOFXOGBR

An emerging theme in this blog is Möbius systems, ones that can be aromatic or antiaromatic. Rzepa has led the way here, especially in examining annulenes with a twisted structure. Along with Schleyer and Schaefer, they have now explored a series of Möbius annulenes.¹ The particularly novel aspect of this new work is the examination of higher-order Möbius systems. In the commonly held notion of the Möbius strip, the strip contains a single half twist. Rzepa points out that the notion of twist must be considered as two parts, a part due to torsions and a part due to writhe.² We can think of the Möbius strip as formed by a ladder where the ends are connect such that the left bottom post connects with the top right post and the bottom right post connects with the top left post. Let’s now consider the circle created by joining the midpoints of each rug of the ladder. If this circle lies in a plane, then the torsion is π/N where N is the number of rungs in the ladder. But, the collection of midpoints does not have to lie in a plane, and if these points distort out of plane, that’s writhe and allows for less torsion in the strip.The sum of these two parts is called L_k and it will be an integral multiple of π. So the common Möbius strip has L_k = 1.

An example of a molecular analogue of the common Möbius strip is the annulene C₉H₉⁺ (1) – see figure 1. But Möbius strips can have more than one twist. Rzepa, Schleyer, and Schaefer have found examples with L_k = 2, 3, or 4. Examples are C₁₄H₁₄ (2) with one full twist (L_k = 2, two half twists), C₁₆H₁₆^2- (3) with three half twists, and C₂₀H₂₀²⁺ (4) with four half twists.

1	2
3	4

Figure 1. Structures of annulenes 1-4.

These annulenes with higher-order twisting, namely 2-4, are aromatic, as determined by a variety of measures. For example, all express negative NICS values, all have positive diagmagnetic exaltations, and all express positive isomerization stabilization energies (which are a measure of aromatic stabilization energy).

References

(1) Wannere, C. S.; Rzepa, H. S.; Rinderspacher, B. C.; Paul, A.; Allan, C. S. M.; Schaefer Iii, H. F.; Schleyer, P. v. R., "The Geometry and Electronic Topology of Higher-Order Charged M&oml;bius Annulenes" J. Phys. Chem. A 2009, ASAP, DOI: 10.1021/jp902176a

(2) Fowler, P. W.; Rzepa, H. S., "Aromaticity rules for cycles with arbitrary numbers of half-twists," Phys. Chem. Chem. Phys. 2006, 8, 1775-1777, DOI: 10.1039/b601655c.

The planar substituted cyclooctatetraene 1 has been prepared and characterized.¹ The B3LYP/6-31G(d) optimized geometry is shown in Figure 1.

1

Figure 1. B3LYP/6-31G(d) optimized geometry of 1.

The ¹H NMR spectrum of 1 shows the bridgehead proton has only a small upfield shift (Δδ = 0.18ppm) relative that of 2. This suggests that both molecules have similar degrees of aromaticity/antiaromaticity, and since both molecules display large bond alternation (ΔR = 0.169 Å in 1 and 0.089 Å in 2) one can argue that both paratropic and diatropic ring currents are attenuated in both molecules. However, the NICS value of 1 is 10.6 ppm, indicative of considerable antiaromatic character, though this NICS value is much reduced from that in planar cyclooctatetraene constrained to the ring geometry of 1 (22.1 ppm). Rabinowitz and Komatsu argue that large HOMO-LUMO gap of 1 is responsible for the reduced antiaromatic character of 1.

Though not discussed in their paper, the aromatic stabilization (destabilization) energy of 1 can be computed. I took two approaches, shown in Reactions 1 and 2. The energies of the two reactions are -13.8 kcal mol^-1 for Reaction 1 and -3.4 kcal mol^-1 for Reaction 2. The large exothermicity of Reaction 1 reflects the strain of packing the four bicyclo moieties near each other, forcing the neighboring bridgehead hydrogens to be directed right at each other. The strain is better compensated in Reaction 2 by using 3 as the reference. Since 3 is of C₂ symmetry, some strain relief remains a contributor to the overall reaction energy. Thus it appears that if 1 is antiaromatic, if manifests in little energetic consequence.

Reaction 1

Reaction 2

References

(1) Nishinaga, T.; Uto, T.; Inoue, R.; Matsuura, A.; Treitel, N.; Rabinovitz, M.; Komatsu, K., "Antiaromaticity and Reactivity of a Planar Cyclooctatetraene Fully Annelated with Bicyclo[2.1.1]hexane Units," Chem. Eur. J., 2008, 14, 2067-2074, DOI: 10.1002/chem.200701405

InChIs

1: InChI=1/C24H24/c1-9-2-10(1)18-17(9)19-11-3-13(4-11)21(19)23-15-7-16(8-15)24(23)22-14-5-12(6-14)20(18)22/h9-16H,1-8H2/b19-17-,20-18-,23-21-,24-22-
InChIKey=PUZMOHQGDBIGOO-LEYBOLSUBU

2: InChI=1/C18H18/c1-7-2-8(1)14-13(7)15-9-3-11(4-9)17(15)18-12-5-10(6-12)16(14)18/h7-12H,1-6H2
InChIKey=ULLLVKXTLZQQFF-UHFFFAOYAL

3: InChI=1/C14H16/c1-7-9-3-11(4-9)13(7)14-8(2)10-5-12(14)6-10/h9-12H,1-6H2/b14-13-
InChIKey=CSIHJUFBXMYVBH-YPKPFQOOBF

Rzepa has published another study of Möbius aromaticity.¹ Here he examines the [14]annulene 1 using the topological method (AIM) and NICS. The B3LYP/6-31G(d) optimized structures of 1, the transition state 3 and product of the 8-e^– electroclization 2 are shown in Figure 1.

1 (0.0)

3 (4.56)

2 (0.07)

Figure 1. B3LYP/6-31G(d) optimized structures and relative energies (kcal mol^-1) of 1-3.¹

The topological analysis of 1 reveals a number of interesting features of the density. First, there are two bond critical points that connect the carbon atoms that cross over each other in the lemniscate structure 1 (these bond paths are drawn as the dashed lines in Scheme 1, connecting C₁ to C₈ and C₇ to C₁₄). These bond critical points have a much smaller electron density than for a typical C-C bond. With these added bond critical points come additional ring points, but not the anticipated 3 ring critical points. There is a ring critical point for the quasi-four member ring (C₁-C₁₄-C₇-C₈-C₁), but the expected ring point for each of the two 8-member ring bifurcate into two separate ring critical points sandwiching a cage critical point!

Scheme 1

Rzepa argues that the weak bonding interaction across the lemniscates is evidence for Möbius homoaromaticity in each half of 1. The NICS value at the central ring critical point is -18.6 ppm, reflective of overall Möbius aromaticity. But the NICS values at the 8-member ring ring critical points of -8.6 ppm and the cage critical points (-7.9 ppm) provide support for the Möbius homoaromaticity.

Transition state 3 corresponds to motion along the bond path of those weak bonds along either C₁-C₈ or C₇-C₁₄. This leads to forming the two fused eight-member rings of 2. An interesting thing to note is that there is only one transition state connecting 1 and 2 – even though one might think of the electrocyclization occurring in either the left or right ring. (Rzepa discusses this in a nice J. Chem. Ed. article.²) This transition state 3 is stabilized by Möbius aromaticity.

As an aside, Rzepa has once again made great use of the web in supplying a great deal of information through the web-enhanced object in the paper. As in the past, ACS continues to put this behind the subscriber firewall instead of considering it to be supporting material, which it most certainly is and should therefore be available to all.

References

(1) Allan, C. S. M.; Rzepa, H. S., "Chiral Aromaticities. AIM and ELF Critical Point and NICS Magnetic Analyses of Moöbius-Type Aromaticity and Homoaromaticity in Lemniscular Annulenes and Hexaphyrins," J. Org. Chem., 2008, 73, 6615-6622, DOI: 10.1021/jo801022b.

(2) Rzepa, H. S., "The Aromaticity of Pericyclic Reaction Transition States" J. Chem. Ed. 2007, 84, 1535-1540, http://www.jce.divched.org/Journal/Issues/2007/Sep/abs1535.html.

InChIs

1:
InChI=1/C14H14/c1-2-4-6-8-10-12-14-13-11-9-7-5-3-1/h1-14H/b2-1-,3-1-,4-2-,5-3-,6-4-,7-5+,8-6+,9-7-,10-8+,11-9-,12-10+,13-11-,14-12-,14-13-
InChIKey= RYQWRHUSMUEYST-YGYPEFQEBU

2: InChI=1/C14H14/c1-2-6-10-14-12-8-4-3-7-11-13(14)9-5-1/h1-14H/b2-1-,4-3-,9-5-,10-6-,11-7-,12-8-/t13-,14+
InChIKey= AMYHCQKNURYOBO-RFCQUTFOBS

In their continuing efforts to build novel aromatic systems, Siegel and Baldridge report the preparation of the decapropyl analogue of the per-ethynylated corrannulene 1.¹ They were hoping that this might cyclize to the bowl 2. It is however stable up to 100 °C, however, the analogue 3 was obtained in the initial preparation of decapropyl-1.

The B3LYP/cc-pVDZ optimized structures of 1 and 3 are shown in Figure 1. 1 is bowl-shaped, reflecting the property of corranulene, but interestingly 3 is planar. The geometry of the {10]annulene is interesting as it is more consistent with the alkynyl resonance form B.

1

3

Figure 1. B3LYP/cc-pVDZ optimized structures of 1 and 3.¹

Siegel and Baldridge speculate that the conversion of 1 → 3 occurs by first undergoing the Bergman cyclization to give 4, which then opens to give 3. Unfortunately, they did not compute the activation barrier for this process. They do suggest that further cyclization to give the hoped for 2 might be precluded by the long distances between radical center and neighboring alkynes in 4, but the radicals are too protected to allowing trapping by the solvent, allowing for the formation of 3.

References

(1) Hayama, T.; Wu, Y. T.; Linden, A.; Baldridge, K. K.; Siegel, J. S., "Synthesis, Structure, and Isomerization of Decapentynylcorannulene: Enediyne Cyclization/Interconversion of C₄₀R₁₀ Isomers," J. Am. Chem. Soc., 2007, 129, 12612-12613 DOI: 10.1021/ja074403b.

InChIs

1: InChI=1/C40H10/c1-11-21-22(12-2)32-25(15-5)26(16-6)34-29(19-9)30(20-10)35-28(18-8)27(17-7)33-24(14-4)23(13-3)31(21)36-37(32)39(34)40(35)38(33)36/h1-10H

2: InChI=1/C40H10/c1-2-12-14-5-6-16-18-9-10-20-19-8-7-17-15-4-3-13-11(1)21-22(12)32-24(14)26(16)34-29(18)30(20)35-28(19)27(17)33-25(15)23(13)31(21)36-37(32)39(34)40(35)38(33)36/h1-10H

3: InChI=1/C40H12/c1-9-23-25(11-3)33-27(13-5)29(15-7)35-30(16-8)28(14-6)34-26(12-4)24(10-2)32-22-20-18-17-19-21-31(23)36-37(32)39(34)40(35)38(33)36/h1-8,17-18,31-32H/b18-17-

Castro and Karney¹ previously predicted a Möbius aromatic transition state for the π-bond shift in [12]annulene (see Chapter 2.4.3.1), a process they termed “twist-couple bond shifting”. In late 2006 they turned their attention to the conformational surface of [16]annulene, searching again for Möbius aromatic ground or transition states.²

Oth synthesized [16]annulene by the photolysis of cycloctatetraene dimer. He observed two isomers 1a and 2a in a 83:17 ratio³ at -140 °C, with a barrier⁴ of 10.3 kcal mol^-1 separating them. The ¹H NMR spectrum at -30 °C shows only one signal. The equivalence of all of the protons implicates rapid conformational changes and bond shifting, as suggested in Scheme 1. Also noted was that these conversions, including the configuration change from 1 to 2, have barriers much lower than for the electrocyclization of Reaction 1 of about 22 kcal mol^-1.⁵

Scheme 1
	Reaction 1

Following on the results from their [12]annulene study, Castro and Karney optimized geometries at BH&HLYP/6-311+G(d,p). Since, as we discussed in Chapter 2.4.3.1, relative energies of annulene conformations are very sensitive to the computational method and basis set, they determined estimated CCSD(T)/cc-pVDZ energies, which I will call E_est, according to a prescription proposed by Bally and MacMahon,⁶ namely

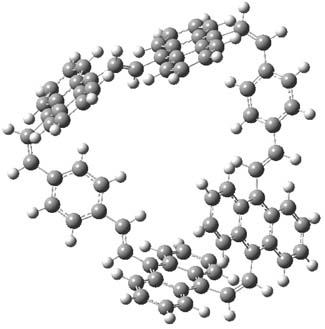
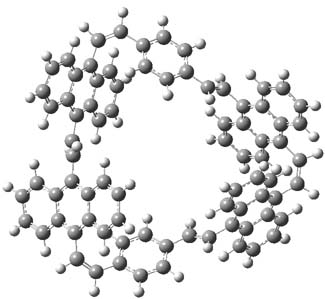
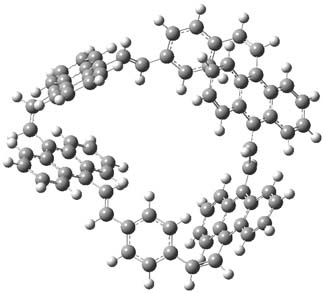
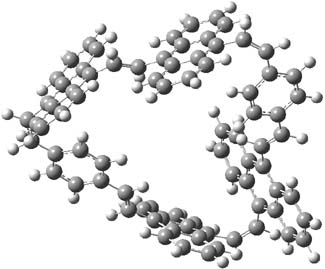
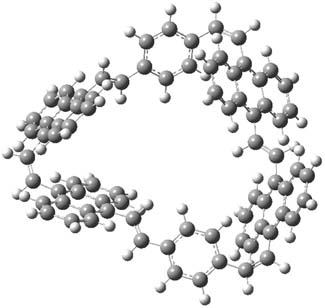
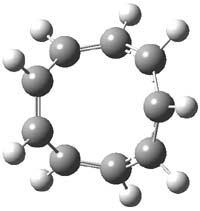
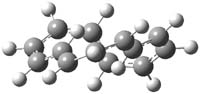
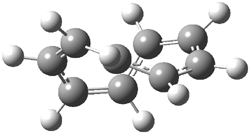
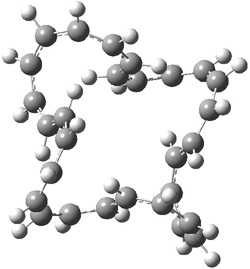
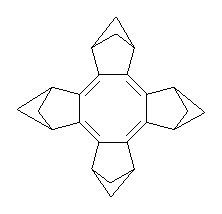
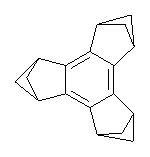
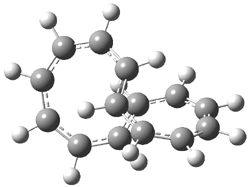
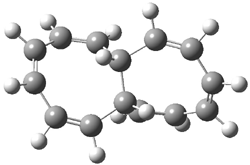
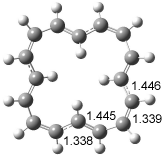
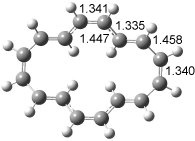
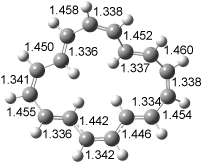
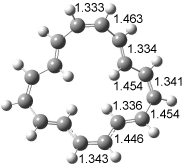
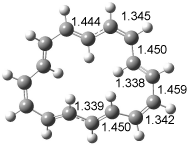
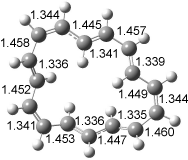
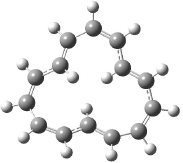
The optimized structures of 1a and 2a are drawn in Figure 1. Both molecules are not planar, their bond lengths are clearly alternating, and their NICS(0) values are +6.4 ppm (1a) and +7.3 ppm (2a), all evidence that neither molecule is aromatic. 1a is predicted to be 0.8 kcal mol^-1 lower in energy than 2a, consistent with experiment.

1a (0.0) xyz file	1b (5.6) xyz file
1c (5.4) xyz file	1d (7.7) xyz file
2a (0.8) xyz file	2b (4.1) xyz file
TS-1c2b (13.7) xyz file

Figure 1. BH&HLYP/6-311+G(d,p) optimized geometries and relative energies (kcal mol^-1) based on E_est.²

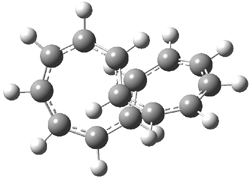
The conformational change 1a → 1a’ is a multi-step process. This is in contrast to [12]annulene where this change occurs via a concerted mechanism. So, 1a first converts to 1c through a barrier of 7.9 kcal mol^-1. The path now splits; 1b can next be formed with a barrier of 9.4 kcal mol^-1 to give 1c’ or 1d can be formed through a barrier of 7.7 kcal mol^-1 to produce 1c’. 1c’ converts to 1a’ with a barrier of 7.9 kcal mol^-1. The structures of the intermediates and their relative energies are shown in Figure 1.

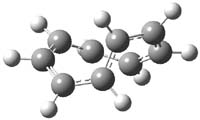
The conversion of 1 to 2 takes place through the transition state TS-1c2b that actually connects isomer 1c to 2b. This structure, shown in Figure 1, exhibits little bond alternation and has a NICS(0) value of -14.2, both strongly suggestive of Möbius aromatic character. Aromaticity should also imply energetic stabilization; TS-1c2b lies only 13.7 kcal mol^-1 above 1a. This barrier is less than that predicted for the twist-coupled bond shift in either [10]annulene or [12]annulene.

The highest barrier for the various interconversions indicated in Scheme 1 is the barrier associated with TS-1c2b. This barrier (13.7 kcal mol^-1) is significantly lower that the activation energy for Reaction 1 (22 kcal mol^-1). These computations confirm that the scrambling of the protons of [16]annulene is due to the rapid rearrangements of Scheme 1. Furthermore, the computations demonstrate that the key step is a twist-coupled bond shift that is facilitated by the Möbius aromatic character of its transition state.

Since the configuration change in [12]- and [16]annulene proceeds with a bond-shifting Möbius aromatic bond shifting transition state, might not the configuration change of [14]annulene proceed through a Möbius antiaromatic bond shifting transition state? In 2007, Castro and Karney⁷ answered this question in the affirmative.

Consistent with their previous studies, geometries were optimized at UBH&HLYP/6-311+G**. The unrestricted method is necessary since the expected antiaromatic transition state will have singlet radical character. In order to obtain reasonable energies, CASPT2(14,14)/cc-pVDZ single-point computations were employed.

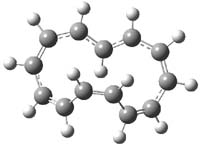
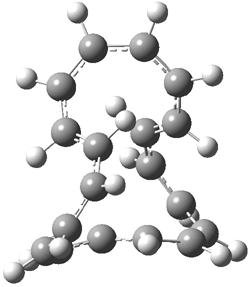
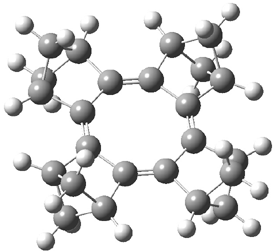
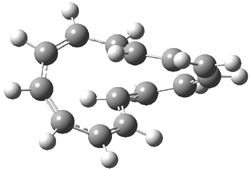
[14]annulene must undergo two conformational changes (3a-c) before the bond shift/configuration change can occur through transition state 4 to give 5. Note that this process changes the number of cis and trans double bonds. This overall process is shown in Figure 2. The optimized structures of 3c, 4, and 5 are shown in Figure 3.

Figure 2. CASPT2(14,14)/cc-pVDZ// UBH&HLYP/6-311+G** relative energies of stable structures along the pathway for configuration change of [14]annulene.

The computed barrier for the configuration change (through 4) is computed to be 19.3 kcal mol-1, in very reasonable agreement with the experimental value⁴ of 21.3 kcal mol-1.

3c

4

5

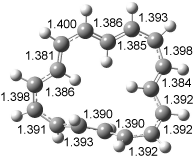
Figure 3. UBH&HLYP/6-311+G** optimized geometries of 3c, 4, and 5.⁷

Based on its magnetic properties, transition state 4 has decided antiaromatic character. Its computed NICS(0) value is +19.0 ppm. Compare this to the NICS(0) values for 3a and 5 of -8.0 and -5.0 ppm, respectively. In addition, the computed chemical shifts of the two interior protons are very downfield, 26.4 and 26.7 ppm.

InChI

1: InChI=1/C16H16/c1-2-4-6-8-10-12-14-16-15-13-11-9-7-5-3-1/h1-16H/b2-1-,3-1-,4-2+,5-3+,6-4+,7-5+,8-6-,9-7-,10-8-,11-9-,12-10+,13-11+,14-12+,15-13+,16-14-,16-15-

2: InChI=1/C16H16/c1-2-4-6-8-10-12-14-16-15-13-11-9-7-5-3-1/h1-16H/b2-1-,3-1-,4-2+,5-3+,6-4+,7-5+,8-6-,9-7+,10-8+,11-9+,12-10+,13-11-,14-12-,15-13-,16-14+,16-15+

3: InChI=1/C14H14/c1-2-4-6-8-10-12-14-13-11-9-7-5-3-1/h1-14H/b2-1-,3-1-,4-2+,5-3+,6-4+,7-5+,8-6-,9-7-,10-8+,11-9+,12-10+,13-11+,14-12-,14-13-

5: InChI=1/C14H14/c1-2-4-6-8-10-12-14-13-11-9-7-5-3-1/h1-14H/b2-1-,3-1-,4-2-,5-3+,6-4+,7-5+,8-6+,9-7-,10-8-,11-9-,12-10-,13-11-,14-12+,14-13+

References

(1) Castro, C.; Karney, W. L.; Valencia, M. A.; Vu, C. M. H.; Pemberton, R. P., “Möbius Aromaticity in [12]Annulene: Cis-Trans Isomerization via Twist-Coupled Bond Shifting,” J. Am. Chem. Soc. 2005, 127, 9704-9705, DOI: 10.1021/ja052447j.

(2) Pemberton, R. P.; McShane, C. M.; Castro, C.; Karney, W. L., “Dynamic Processes in [16]Annulene: Change,” J. Am. Chem. Soc. 2006, 128, 16692-16700, DOI: 10.1021/ja066152x

(3) Oth, J. F. M.; Anthoine, G.; Gilles, J.-M., “Le dianion du [16] annulene,” Tetrahedron Lett. 1968, 9, 6265-6270, DOI: 10.1016/S0040-4039(00)75449-9.

(4) Oth, J. F. M., “Conformational Mobility and Fast Bond Shift in the Annulenes,” Pure Appl. Chem. 1971, 25, 573-622.

(5) Schroeder, G.; Martin, W.; Oth, J. F. M., “Thermal and Photochemical Behavior of a [16]Annulene,” Angew. Chem. Int. Ed. Engl. 1967, 6, 870-871, DOI: 10.1002/anie.196708701.

(6) Matzinger, S.; Bally, T.; Patterson, E. V.; McMahon, R. J., “The C₇H₆ Potential Energy Surface Revisited: Relative Energies and IR Assignment,” J. Am. Chem. Soc. 1996, 118, 1535-1542, DOI: 10.1021/ja953579n.

(7) Moll, J. F.; Pemberton, R. P.; Gutierrez, M. G.; Castro, C.; Karney, W. L., “Configuration Change in [14]Annulene Requires Möbius Antiaromatic Bond Shifting,” J. Am. Chem. Soc. 2007, 129, 274-275, DOI: 10.1021/ja0678469.