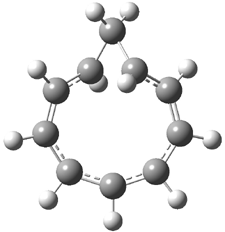
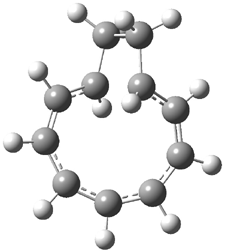
Rzepa has extended the concept of Möbius aromaticity to homoaromaticity.1 1 is the homoaromatic analogue of the tropylium cation. Topoligical electron density analysis, also known as Atoms-In-Molecules (AIM), indicates no bond path connecting C1and C7. However, the NICS value at the ring critical point of 1 is -11.5 ppm, indicative of aromaticity. 2 is the potential Möbius aromatic analogue of 1. Unlike 1 which has a plane of symmetry, 2 has a C2 rotational axis of symmetry, as anticipated for a Möbius homoaromatic compound. However, there is no bond path connecting C1 with C9. But, the NICS value at the ring critical point of 2 is -11.3 ppm, supporting the notion of aromatic character! Suprisingly, the AIM analysis of the larger homologue 3 does have a bond path connecting C1 to C9, even though the distance separating these compounds is larger than in 2! Again the NICS value for 3 is negative (-9.8) and so it certainly appears to be Möbius homoaromatic.

The B3LYP/aug-cc-pVYZ structures of 1-3 are shown in Figure 1. As is Rzepa’s practice, he provides an extensive collection of data on the molecules he reports making great use of electronic depositories, and it looks like the ACS has now moved this “web-enhanced table” out into the open part of its web site: http://pubs.acs.org/doi/suppl/10.1021/ct8001915/suppl_file/index.html.
|
1 |
2 |
|
3 |
|
Figure 1. B3LYP/aug-cc-pVYZ optimized structures of 1-3.1
References
(1) Allan, C. S. M.; Rzepa, H. S., "Chiral Aromaticities. A Topological Exploration of Möbius Homoaromaticity," J. Chem. Theory Comput., 2008, 4, 1841-1848, DOI: 10.1021/ct8001915
InChIs
1: InChI=1/C8H9/c1-2-4-6-8-7-5-3-1/h1-7H,8H2/q+1/b2-1-,5-3-,6-4-
InChIKey=ZINXKSGXPFSBNB-XCADPSHZBA
2: InChI=1/C10H11/c1-2-4-6-8-10-9-7-5-3-1/h1-9H,10H2/q+1/b2-1-,5-3-,6-4-,9-7-
InChIKey=HBJCUFQWAIKURE-BWYSQNKRBE
3: InChI=1/C11H13/c1-2-4-6-8-10-11-9-7-5-3-1/h1-9H,10-11H2/q+1/b2-1-,5-3-,6-4-,9-7-InChIKey=LUGAIBOLHSLVBJ-BWYSQNKRBF


Henry Rzepa responded on 14 Feb 2009 at 6:19 am #
I might add that the presence or absence of the so-called AIM bond critical points as indicating “bonding” continues to be controversial. At its origin may be an interesting topological relation, the Poincare-Hopf condition, which states NCP – BCP + RCP – CCP = 1 (where N=nuclear, B=bond, R=ring and C=cage critical points). The key here is that BCP and RCP have opposite signs. If an BCP and a RCP become physically close to each other, they can in fact merge, and mutually annihilate each other. This is in fact what happens in many so called homo-aromatic systems, such as molecules 1 and 2. With molecule 3, with a larger ring, the BCP and RCP are now more separated, and their self-destruction does not occur. So in fact the presents of a BCP in 3, and its absence in 1 or 2 does not actually have any deep significance for what we call a “bond”. Perhaps a better metric is the so-called disynaptic basin found in the ELF function, which can be integrated, and which reveals an integrated electron density of around 1 electron for these homo-aromatic bonds, exactly what a simple minded explanation would predict.
I have elaborated the above somewhat in a pedagogic article which will hopefully appear in J. Chem. Ed. in the coming months.
sbachrach responded on 16 Feb 2009 at 10:06 am #
Henry,
I have always had my doubts about Bader’s contention that the existence of a bond path in a local energy minimum structure is necessary and sufficient for a chemical bond. In some early work of mine, we discovered organolithium compounds with more than 4 bond paths terminating at carbon – as many as 9 in some cases – see 10.1021/ja00254a004 and 10.1021/ja00280a057.