A couple of additional papers have pointed out systematic problems with using DFT and offer guidelines for methods that provide accurate results. These complement my previous posts on the subject Problems with DFT and Problems with DFT – an Update.
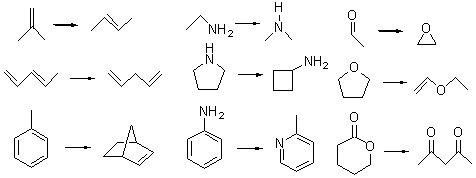
Grimme1 takes the approach of benchmarking methods and basis sets using isomerization energies, examples of which are shown in Scheme 1. Computed isomerization reaction energies are compared against experimental values or, in a few cases, against extrapolated CCSD(T) energies using cc-pVXZ (X=D-T or X=T-Q). This extrapolation technique2 is a way to estimate the complete basis set energy.
Scheme 1.
In terms of basis set, the error systematically decreases with increasing size of the basis set when the SCS-MP2 method is used to compute the energies. Surprisingly, the error is essentially constant for all the basis sets with B3LYP. The root-mean-square deviation and maximum error for the isomerization energies computed with the TZV(2df,2pd) basis set and a variety of different methods are listed in Table 1. Both CCSD(T) and SCS-MP2 provide truly excellent results. Since the later method is much more computationally efficient that the former, Grimme argues that this is really the method of choice for accurate energies. DFT methods vary in their performance, with no discernable trend based on what type of DFT it is (i.e. meta-GGA, hybrid GGA, or hybrid meta-GGA). Of no surprise, based on lots of recent studies (including those blogged about in ), the performance of B3LYP is likely to be problematic.
Table 1. Errors in Computed Isomerization Energies (kcal/mol)
|
|
||
|
Method |
rms |
Max. error |
|
CCSD(T) |
0.95 |
2.3 |
|
SCS-MP2 |
1.27 |
2.6 |
|
mPW2-PLYP |
1.83 |
6.1 |
|
MP2 |
2.04 |
6.2 |
|
PBE0 |
2.45 |
7.0 |
|
PBE |
2.54 |
7.3 |
|
B3LYP |
3.27 |
10.2 |
|
TPSS |
3.46 |
11.4 |
|
HF |
3.79 |
12.9 |
|
|
||
In a related study, Bond3 explores the ability of the composite methods to predict enthalpies and free energies of formation for a set of nearly 300 compounds. Bond makes use of isodesmic and homodesmotic reactions (discussed in Chapter 2). His results for the mean absolute deviations of ΔH are given in Table 2. All of the composite methods (see Chapter 1.2.6) provide quite acceptable results. Once again, B3LYP is shown to be incapable of predicting accurate energies.
Table 2. Mean average deviation in predicted heats of formation compared
to literature values.
|
|
||
|
Method |
MAD(ΔH) |
|
|
G2 |
3.5 |
|
|
G2MP2 |
3.7 |
|
|
G3 |
3.1 |
|
|
G3MP2 |
3.2 |
|
|
G3B3 |
2.9 |
|
|
CBS-QB3 |
4.5 |
|
|
B3LYP/6-311+G(3df,2p) |
16.4 |
|
References
(1) Grimme, S.; Steinmetz, M.; Korth, M., "How to Compute Isomerization Energies of Organic Molecules with Quantum Chemical Methods," J. Org. Chem., 2007, 72, 2118-2126, DOI: 10.1021/jo062446p.
(2) Helgaker, H.; Klopper, W.; Koch, H.; Noga, J., "Basis-Set Convergence of Correlated Calculations on Water," J. Chem. Phys., 1997, 106, 9639-9646, DOI: 10.1063/1.473863
(3) Bond, D., "Computational Methods in Organic Thermochemistry. 1. Hydrocarbon Enthalpies and Free Energies of Formation," J. Org. Chem. 2007, 72, 5555-5566, DOI: 10.1021/jo070383k

Computational Organic Chemistry » Errors in DFT: computation of the Diels-Alder reaction responded on 01 Dec 2008 at 9:37 am #
[…] Concern about the use of DFT for general use in organic chemistry remains high; see my previous posts (1, 2, 3). Houk has now examined the reaction enthalpies of ten simple Diels-Alder reactions using a variety of functionals in the search for the root cause of the problem(s).1 […]
Computational Organic Chemistry » Origin of DFT failure responded on 19 May 2009 at 8:11 am #
[…] with some seemingly straightforward reactions (as discussed in these previous blog posts: A, B, C, D, E, F) has become a bit clearer. Brittain and co-workers have identified the culprit.1 They […]