Can vibrational spectroscopy be used to identify stereoisomers? Medel, Stelbrink, and Suhm have examined the vibrational spectra of (+)- and (-)-α-pinene, (±)-1, in the presence of four different chiral terpenes 2-5.¹ They recorded gas phase spectra by thermal expansion of a chiral α-pinene with each chiral terpene.

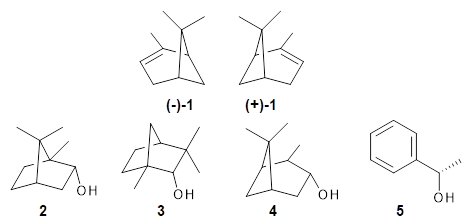
For the complex of 4 with (+)-1 or (-)-1 and 5 with (+)-1 or (-)-1, the OH vibrational frequency is identical for the two different stereoisomers. However, the OH vibrational frequencies differ by 2 cm^-1 with 3, and the complex of 3/(+)-1 displays two different OH stretches that differ by 11 cm^-1. And in the case of the complex of α-pinene with 2, the OH vibrational frequencies of the two different stereoisomers differ by 11 cm^-1!

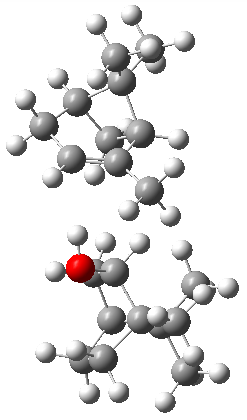
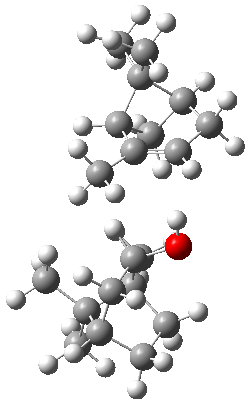
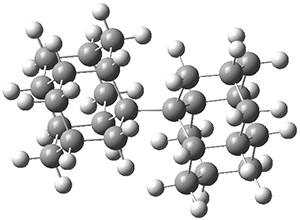
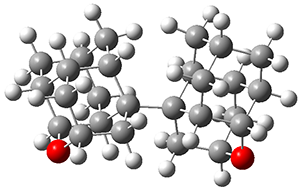
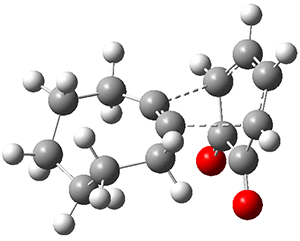
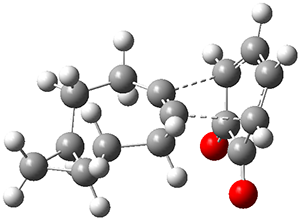
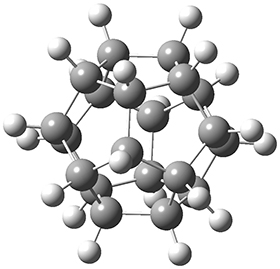
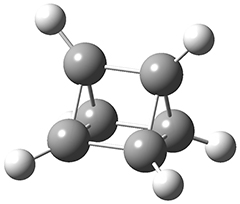
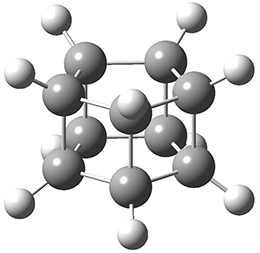
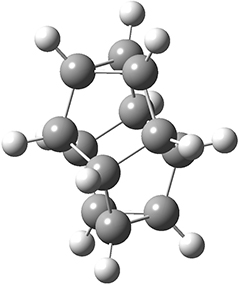
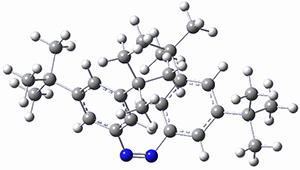
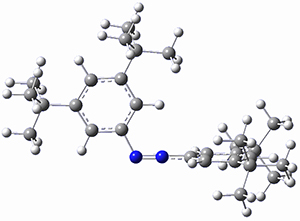
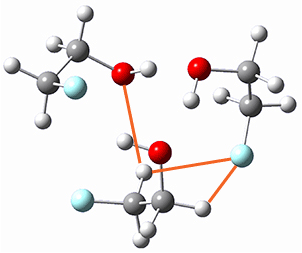
The B3LYP-D3(BJ)/def2-TZVP optimized geometry of the 2/(+)-1 and 2/(-)-1 complexes are shown in Figure 2, and some subtle differences in sterics and dispersion give rise to the different vibrational frequencies.

Figure 2. B3LYP-D3(BJ)/def2-TZVP optimized geometry of the 2/(+)-1 and 2/(-)-1

Of interest to readers of this blog will be the DFT study of these complexes. The authors used three different well-known methods – B3LYP-D3(BJ)/def2-TZVP, M06-2x/def2-TZVP, and ωB97X-D/def2-TZVP – to compute structures and (most importantly) predict the vibrational frequencies. Interestingly, M06-2x/def2-TZVP and ωB97X-D/ def2-TZVP both failed to predict the vibrational frequency difference between the complexes with the two stereoisomers of α-pinene. However, B3LYP-D3(BJ)/def2-TZVP performed extremely well, with a mean average error (MAE) of only 1.9 cm^-1 for the four different terpenes. Using this functional and the larger may-cc-pvtz basis set reduced the MAE to 1.5 cm^-1 with the largest error of only 2.5 cm^-1.

As the authors note, these complexes provide some fertile ground for further experimental and computational study and benchmarking.

Reference

1. Medel, R.; Stelbrink, C.; Suhm, M. A., “Vibrational Signatures of Chirality Recognition Between α-Pinene and Alcohols for Theory Benchmarking.” Angew. Chem. Int. Ed. 2019, 58, 8177-8181, DOI: 10.1002/anie.201901687.

InChIs

(-)-1, (-)-α-pinene: InChI=1S/C10H16/c1-7-4-5-8-6-9(7)10(8,2)3/h4,8-9H,5-6H2,1-3H3/t8-,9-/m0/s1
InChIKey=GRWFGVWFFZKLTI-IUCAKERBSA-N

(+)-1, (-)-α-pinene: InChI=1S/C10H16/c1-7-4-5-8-6-9(7)10(8,2)3/h4,8-9H,5-6H2,1-3H3/t8-,9-/m1/s1
InChIKey=GRWFGVWFFZKLTI-RKDXNWHRSA-N

2, (-)borneol: InChI=1S/C10H18O/c1-9(2)7-4-5-10(9,3)8(11)6-7/h7-8,11H,4-6H2,1-3H3/t7-,8+,10+/m0/s1
InChiKey=DTGKSKDOIYIVQL-QXFUBDJGSA-N

3, (+)-fenchol: InChI=1S/C10H18O/c1-9(2)7-4-5-10(3,6-7)8(9)11/h7-8,11H,4-6H2,1-3H3/t7-,8-,10+/m0/s1
InChIKey=IAIHUHQCLTYTSF-OYNCUSHFSA-N

4, (-1)-isopinocampheol: InChI=1S/C10H18O/c1-6-8-4-7(5-9(6)11)10(8,2)3/h6-9,11H,4-5H2,1-3H3/t6-,7+,8-,9-/m1/s1
InChIKey=REPVLJRCJUVQFA-BZNPZCIMSA-N

5, (1S)-1-phenylethanol: InChI=1S/C8H10O/c1-7(9)8-5-3-2-4-6-8/h2-7,9H,1H3/t7-/m0/s1
InChIKey=WAPNOHKVXSQRPX-ZETCQYMHSA-N

Selecting the appropriate density functional for one’s molecular system at hand is often a very confounding problem, especially for non-expert or first-time users of computational chemistry. The DFT zoo is vast and confusing, and perhaps what makes the situation worse is that there is no lack of benchmarking studies. For example, I have made more than 30 posts on benchmark studies, and I made no attempt to be comprehensive over the past dozen years!

One such benchmark study that I missed was presented by Mardirossian and Head-Gordon in 2017.¹ They evaluated 200 density functional using the MGCDB84 database, a combination of data from a number of different groups. They make a series of recommendations for local GGA, local meta-GGA, hybrid GGA, and hybrid meta-GGA functionals. And when pressed to choose just one functional overall, they opt for ωB97M-V, a range-separated hybrid meta-GGA with VV10 nonlocal correlation.

Georigk and Mehta² just recently offer a review of the density functional zoo. Leaning heavily on benchmark studies using the GMTKN55³ database, they report a number of observations. Of no surprise to readers of this blog, their main conclusion is that accounting for London dispersion is essential, usually through some type of correction like those proposed by Grimme.

These authors also note the general disparity between the most accurate, best performing functional per the benchmark studies and the results of the DFT poll conducted for many years by Swart, Bickelhaupt and Duran. It is somewhat remarkable that PBE or PBE0 have topped the poll for many years, despite the fact that many newer functionals perform better. As always, when choosing a functional caveat emptor.

References

1.  Mardirossian, N.; Head-Gordon, M., “Thirty years of density functional theory in computational chemistry: an overview and extensive assessment of 200 density functionals.” Mol. Phys. 2017, 115, 2315-2372, DOI: 10.1080/00268976.2017.1333644.

2. Goerigk, L.; Mehta, N., “A Trip to the Density Functional Theory Zoo: Warnings and Recommendations for the User.” Aust. J. Chem. 2019, ASAP, DOI: 10.1071/CH19023.

3. Goerigk, L.; Hansen, A.; Bauer, C.; Ehrlich, S.; Najibi, A.; Grimme, S., “A look at the density functional theory zoo with the advanced GMTKN55 database for general main group thermochemistry, kinetics and noncovalent interactions.” Phys. Chem. Chem. Phys. 2017, 19, 32184-32215, DOI: 10.1039/C7CP04913G.

Pericyclic reactions remain a fruitful area of research despite the seminal publication of the Woodward-Hoffmann rules decades ago. Here are two related papers of pericyclic reactions that violate the Woodward-Hoffmann rules.

First, Solomek, Ravat, Mou, Kertesz, and Jurícek reported on the thermal and photochemical electrocyclization reaction of diphenylcetherene 1a.¹ Though they were not able to directly detect the intermediate 2, through careful examination of the photochemical reaction, they were able to infer that the thermal cyclization goes via the formally forbidden conrotatory pathway (see Scheme 1).

Scheme 2.

Kinetic studies estimate the activation barrier is 14.1 kcal mol^-1. They performed DFT computations of the parent 1b using a variety of functionals with both restricted and unrestricted wavefunctions. The allowed pathway to 2syn is predicted to be greater than 27 kcal mol^-1, while the formally forbidden pathway to 2anti is estimated to have a lower barrier of about 23 kcal mol^-1. The two transition states for these different pathways are shown in Figure 1, and the sterics that force a helical structure to 1 help make the forbidden pathway more favorable.

Figure 1. (U)B3LYP/6-31G optimized geometries of the transition states taking 1 into 2.

Nonetheless, all of the DFT computations significantly overestimate the activation barrier. The authors make the case that a low-lying singlet excited state results in an early conical intersection that reduces the symmetry from C₂ to C₁. In this lower symmetry pathway, all of the states can mix, leading to a lower barrier. However, since DFT is intrinsically a single Slater configuration, the mixing of the other states is not accounted for, leading to the overestimated barrier height.

In a follow up study, this group examined the thermal and photo cyclization of 13,14-dimethylcethrene 4.² The added methyl groups make the centhrene backbone more helical, and this precludes the formal allowed disrotatory process. The methyl groups also prohibit the oxidation that occurs with 1, driven by aromatization, allowing for the isolation of the direct product of the cyclization 5. This anti stereochemistry is confirmed by NMR and x-ray crystallography. The interconversion between 4 and 5 can be controlled by heat and light, making the system an interesting photoswitch.

Also of interest is the singlet-triplet gap of 1 and 4. The DFT computed ΔE_ST is about 10 kcal mol^-1 for 4, larger than the computed value of 6 kcal mol^-1 for 1b. The EPR of 1b does show a signal while that of 4 has no signal. To assess the role of the methyl group, they computed the singlet triplet gaps for 1b and 4 at two different geometries: where the distance between the carbons bearing the methyl groups is that in 1b (3.03 Å) and in 4 (3.37 Å). The lengthening of this distance by the methyl substituents is due to increased helical twist in 4 than in 1b. For 1b, the gap increases with twisting, from 7.1 to 8.3 kcal mol^-1, while for 4 the gap increases by 1.8 kcal mol^-1 with the increased twisting. This change is less than the effect of methyl substitution, which increases the gap by 2.2 kcal mol^-1 at the shorter distance and 2.8 kcal mol^-1 at the longer distance. Thus, the electronic (orbital) effect of methyl substitution affects the singlet-triplet gap more than the geometric twisting.

References

1) Šolomek, T.; Ravat, P.; Mou, Z.; Kertesz, M.; Juríček, M., "Cethrene: The Chameleon of Woodward–Hoffmann Rules." J. Org. Chem. 2018, 83, 4769-4774, DOI: 10.1021/acs.joc.8b00656.

2) Ravat, P.; Šolomek, T.; Häussinger, D.; Blacque, O.; Juríček, M., "Dimethylcethrene: A Chiroptical Diradicaloid Photoswitch." J. Am. Chem. Soc. 2018, 140, 10839-10847, DOI: 10.1021/jacs.8b05465.

InChIs

1b: InChI=1S/C28H16/c1-5-17-7-3-11-23-25(17)19(9-1)15-21-13-14-22-16-20-10-2-6-18-8-4-12-24(26(18)20)28(22)27(21)23/h1-16H
InChIKey=GBMHAGKZRAVBDO-UHFFFAOYSA-N

4: InChI=1S/C30H20/c1-17-9-11-19-5-3-7-21-15-23-13-14-24-16-22-8-4-6-20-12-10-18(2)26(28(20)22)30(24)29(23)25(17)27(19)21/h3-16H,1-2H3
InChIKey=MXTVFWTUCPRNIW-UHFFFAOYSA-N

5: nChI=1S/C30H20/c1-29-13-11-17-5-3-7-19-15-21-9-10-22-16-20-8-4-6-18-12-14-30(29,2)28(24(18)20)26(22)25(21)27(29)23(17)19/h3-16H,1-2H3/t29-,30-/m0/s1
InChIKey=SUMMGEBJORQMAI-KYJUHHDHSA-N

Schreiner and Grimme have examined a few compounds (see these previous posts) with long C-C bonds that are found in congested systems where dispersion greatly aids in stabilizing the stretched bond. Their new paper¹ continues this theme by examining 1 (again) and 2, using computations, and x-ray crystallography and gas-phase rotational spectroscopy and electron diffraction to establish the long C-C bond.

The distance of the long central bond in 1 is 1.647 Å (x-ray) and 1.630 Å (electron diffraction). Similarly, this distance in 2 is 1.642 Å (x-ray) and 1.632 Å (ED). These experiments discount any role for crystal packing forces in leading to the long bond.

A very nice result from the computations is that most functionals that include some dispersion correction predict the C-C distance in the optimized structures with an error of no more than 0.01 Å. (PW6B95-D3/DEF2-QZVP structures are shown in Figure 1.) Not surprisingly, HF and B3LYP without a dispersion correction predict a bond that is too long.) MP2 predicts a distance that is too short, but SCS-MP2 does a very good job.

Figure 1. PW6B95-D3/DEF2-QZVP optimized structures of 1 and 2.

References

1) Fokin, A. A.; Zhuk, T. S.; Blomeyer, S.; Pérez, C.; Chernish, L. V.; Pashenko, A. E.; Antony, J.; Vishnevskiy, Y. V.; Berger, R. J. F.; Grimme, S.; Logemann, C.; Schnell, M.; Mitzel, N. W.; Schreiner, P. R., "Intramolecular London Dispersion Interaction Effects on Gas-Phase and Solid-State Structures of Diamondoid Dimers." J. Am. Chem. Soc. 2017, 139, 16696-16707, DOI: 10.1021/jacs.7b07884.

InChIs

1: InChI=1S/C28H38/c1-13-7-23-19-3-15-4-20(17(1)19)24(8-13)27(23,11-15)28-12-16-5-21-18-2-14(9-25(21)28)10-26(28)22(18)6-16/h13-26H,1-12H2
InChIKey=MMYAZLNWLGPULP-UHFFFAOYSA-N

2: InChI=1S/C26H34O2/c1-11-3-19-15-7-13-9-25(19,21(5-11)23(27-13)17(1)15)26-10-14-8-16-18-2-12(4-20(16)26)6-22(26)24(18)28-14/h11-24H,1-10H2
InChIKey=VPBJYHMTINJMAE-UHFFFAOYSA-N

Click chemistry has been used in a broad range of applications. The use of metal catalysts has limited its application to biological system, but the development of strain-promoted cycloaddition to cyclooctyne has opened up click chemistry to bioorthogonal labeling.

An interesting variation on this is the use of 1,2-benzoquinone 1 and substituted analogues as the Diels-Alder diene component. Escorihuela and co-workers have reported on the use of this diene with a number of cyclooctyne derivatives, measuring kinetics and also using computations to assess the mechanism.¹

Their computations focused on two reactions using cyclooctyne 2 and the cyclopropane-fused analogue 3:

They examined these reactions with a variety of density functionals along with some post-HF methods. The transition states of the two reactions are shown in Figure 1. A variety of different density functionals and MP2 are consistent in finding synchronous or nearly synchronous transition states.

Figure 1. B97D/6-311+G(d,p) transition states for Reactions 1 and 2.

In terms of activation energies, all of the DFT methods consistently overestimate the barrier by about 5-10 kcal mol^-1, with B97D-D3 doing the best. MP2 drastically underestimates the barriers, though the SOS-MP2 or SCS-MP2 improve the estimate. Both CCSD(T) and MR-AQCC provide estimates of about 8.5 kcal mol^-1, still 3-4 kcal mol^-1 too high. The agreement between CCSD(T), a single reference method, and MR-AQCC, a multireference method, indicate that the transition states have little multireference character. Given the reasonable estimate of the barrier afforded by B97D-D3, and its tremendous performance advantage over SCS-MP2, CCSD(T) and MR-AQCC, this is the preferred method (at least with current technology) for examining Diels-Alder reactions like these, especially with larger molecules.

References

1) Escorihuela, J.; Das, A.; Looijen, W. J. E.; van Delft, F. L.; Aquino, A. J. A.; Lischka, H.; Zuilhof, H., "Kinetics of the Strain-Promoted Oxidation-Controlled Cycloalkyne-1,2-quinone Cycloaddition: Experimental and Theoretical Studies." J. Org. Chem. 2018, 83, 244-252, DOI: 10.1021/acs.joc.7b02614.

InChIs

1: InChI=1S/C6H4O2/c7-5-3-1-2-4-6(5)8/h1-4H
InChIKey=WOAHJDHKFWSLKE-UHFFFAOYSA-N

2: InChI=1S/C8H12/c1-2-4-6-8-7-5-3-1/h1-6H2
InChIKey=ZPWOOKQUDFIEIX-UHFFFAOYSA-N

3: InChI=1S/C9H12/c1-2-4-6-9-7-8(9)5-3-1/h8-9H,3-7H2
InChIKey=rQDNSAFCVPAMWCJ-UHFFFAOYSA-N

4: InChI=1S/C14H16O2/c15-13-11-7-8-12(14(13)16)10-6-4-2-1-3-5-9(10)11/h7-8,11-12H,1-6H2
InChIKey=OQMYZEFKUMPECV-UHFFFAOYSA-N

5: InChI=1S/C15H16O2/c16-14-12-5-6-13(15(14)17)11-4-2-9-7-8(9)1-3-10(11)12/h5-6,8-9,12-13H,1-4,7H2/t8-,9+,12?,13?
InChIKey=NKDGTIVNLDJQKR-RFZWMSCOSA-N

I recently blogged about a paper arguing that modern density functional development has strayed from the path of improving density description, in favor of improved energetics. The Medvedev paper¹ was met with a number of criticisms. A potential “out” from the conclusions of the work was that perhaps molecular densities do not fare so poorly with more modern functionals, following the argument that better energies might reflect better densities in bonding regions.

The Hammes-Schiffer group have now examined 14 diatomic molecules with the goal of testing just this hypothesis.² They subjected both homonuclear diatomics, like N₂, Cl₂, and Li₂, and heteronuclear diatomics, like HF, LiF, and SC, to 90 different density functionals using the very large aug-cc-pCVQZ basis set. Using the CCSD density as a reference, they examined the differences in the densities predicted by the various functional both along the internuclear axis and perpendicular to it.

The 20 functionals that do the best job in mimicking the CCSD density are all hybrid GGA functionals, along with the sole double hybrid functional included in the study (B2PLYP). These functionals date from 1993 to 2012. The 20 functionals that do the poorest job include functionals from all rung-types, and date from 1980-2012. A very slight upward trend can be observed in the density error increasing with development year, while the error in the dissociation energy clearly is decreasing over time.

They note that six functionals of the Minnesota-type, those that are highly parameterized and of recent vintage, perform very poorly at predicting atomic densities, but do well with the diatomic densities.

Hammes-Schiffer concludes that their diatomic results support the general trend noted by Medvedev’s atomic results, that density description is lagging in more recently developed functionals. I’d add that this trend is not as dramatic for the diatomics as for atoms.

They pose what is really the key question: “Is the purpose to approximate the exact functional or simply to provide chemists with a useful tool for exploring chemical systems?” Since, as they note, the modern highly parameterized functionals have worked so well for predicting energies and geometries, “the observation that many modern functionals produce incorrect densities could be of no great consequence for many studies”. Nonetheless, “the ultimate goal is still to obtain both accurate densities and accurate energies”.

References

1) Medvedev, M. G.; Bushmarinov, I. S.; Sun, J.; Perdew, J. P.; Lyssenko, K. A., "Density functional theory is straying from the path toward the exact functional." Science 2017, 355, 49-52, DOI: 10.1126/science.aah5975.

2) Brorsen, K. R.; Yang, Y.; Pak, M. V.; Hammes-Schiffer, S., "Is the Accuracy of Density Functional Theory for Atomization Energies and Densities in Bonding Regions Correlated?" J. Phys. Chem. Lett. 2017, 8, 2076-2081, DOI: 10.1021/acs.jpclett.7b00774.

“Getting the right answer for the right reason” – how important is this principle when it comes to computational chemistry? Medvedev and co-workers argue that when it comes to DFT, trends in functional development have overlooked this maxim in favor of utility.¹ Specifically, they note that

There exists an exact functional that yields the exact energy of a system from its exact density.

Over the past two decades a great deal of effort has gone into functional development, mostly in an empirical way done usually to improve energy prediction. This approach has a problem:

[It], however, overlooks the fact that the reproduction of exact energy is not a feature of the exact functional, unless the input electron density is exact as well.

So, these authors have studied functional performance with regards to obtaining proper electron densities. Using CCSD/aug-cc-pwCV5Z as the benchmark, they computed the electron density for a number of neutral and cationic atoms having 2, 4, or 10 electrons. Then, they computed the densities with 128 different functionals of all of the rungs of Jacob’s ladder. They find that accuracy was increasing as new functionals were developed from the 1970s to the early 2000s. Since then, however, newer functionals have tended towards poorer electron densities, even though energy prediction has continued to improve. Medvedev et al argue that the recent trend in DFT development has been towards functionals that are highly parameterized to fit energies with no consideration given to other aspects including the density or constraints of the exact functional.

In the same issue of Science, Hammes-Schiffer comments about this paper.² She notes some technical issues, most importantly that the benchmark study is for atoms and that molecular densities might be a different issue. But more philosophically (and practically), she points out that for many chemical and biological systems, the energy and structure are of more interest than the density. Depending on where the errors in density occur, these errors may not be of particular relevance in understanding reactivity; i.e., if the errors are largely near the nuclei but the valence region is well described then reactions (transition states) might be treated reasonably well. She proposes that future development of functionals, likely still to be driven by empirical fitting, might include other data to fit to that may better reflect the density, such as dipole moments. This seems like a quite logical and rational step to take next.

A commentary by Korth³ summarizes a number of additional concerns regarding the Medvedev paper. The last concern is the one I find most striking:

Even if there really are (new) problems, it is as unclear as before how they can be overcome…With this in mind, it does not seem unreasonable to compromise on the quality of the atomic densities to improve the description of more relevant properties, such as the energetics of molecules.

Korth concludes with

In the meantime, while theoreticians should not rest until they have the right answer for the right reason, computational chemists and experimentalists will most likely continue to be happy with helpful answers for good reasons.

I do really think this is the correct take-away message: DFT does appear to provide good predictions of a variety of chemical and physical properties, and it will remain a widely utilized tool even if the density that underpins the theory is incorrect. Functional development must continue, and Medvedev et al. remind us of this need.

References

1) Medvedev, M. G.; Bushmarinov, I. S.; Sun, J.; Perdew, J. P.; Lyssenko, K. A., "Density functional theory is straying from the path toward the exact functional." Science 2017, 355, 49-52, DOI: 10.1126/science.aah5975.

2) Hammes-Schiffer, S., "A conundrum for density functional theory." Science 2017, 355, 28-29, DOI: 10.1126/science.aal3442.

3) Korth, M., "Density Functional Theory: Not Quite the Right Answer for the Right Reason Yet." Angew. Chem. Int. Ed. 2017, 56, 5396-5398, DOI: 10.1002/anie.201701894.

Karton, Schreiner, and Martin have benchmarked the heats of formation of some Platonic Solids and related hydrocarbons.¹ The molecules examined are tetrahedrane 1, cubane 2, dodecahedrane 3, trisprismane 4, pentaprismane 5, and octahedrane 6.

The optimized structures (B3LYP-D3BJ/def2-TZVPP) of these compounds are shown in Figure 1.

1	2
3	4
5	6

Figure 1. B3LYP-D3BJ/def2-TZVPP optimized geometries of 1-6.

Using the W1-F12 and W2-F12 composite methods, the estimated the heats of formation of these hydrocarbons are listed in Table 1. Experimental values are available only for 2 and 3; the computed values are off by about 2 kcal mol^-1, which the authors argue is just outside the error bars of the computations. They suggest that the experiments might need to be revisited.

Table 1. Heats of formation (kcal mol^-1) of 1-6.

They conclude with a comparison of strain energies computed using isogyric, isodesmic, and homodesmotic reactions with a variety of computational methods. Somewhat disappointingly, most DFT methods have appreciable errors compared with the W1-F12 results, and the errors vary depend on the chemical reaction employed. However, the double hybrid method DSD-PBEP86-D3BJ consistently reproduces the W1-F12 results.

References

(1)  Karton, A.; Schreiner, P. R.; Martin, J. M. L. "Heats of formation of platonic hydrocarbon cages by means of high-level thermochemical procedures," J. Comput. Chem. 2016, 37, 49-58, DOI: 10.1002/jcc.23963.

InChIs

1: InChI=1S/C4H4/c1-2-3(1)4(1)2/h1-4H
InChIKey=FJGIHZCEZAZPSP-UHFFFAOYSA-N

2: InChI=1S/C8H8/c1-2-5-3(1)7-4(1)6(2)8(5)7/h1-8H
InChIKey=TXWRERCHRDBNLG-UHFFFAOYSA-N

3: InChI=1S/C20H20/c1-2-5-7-3(1)9-10-4(1)8-6(2)12-11(5)17-13(7)15(9)19-16(10)14(8)18(12)20(17)19/h1-20H
InChIKey=OOHPORRAEMMMCX-UHFFFAOYSA-N

4: InChI=1S/C6H6/c1-2-3(1)6-4(1)5(2)6/h1-6H
InChIKey=RCJOMOPNGOSMJU-UHFFFAOYSA-N

5: InChI=1S/C10H10/c1-2-5-3(1)7-8-4(1)6(2)10(8)9(5)7/h1-10H
InChIKey=TXSUZIHPJIZTJT-UHFFFAOYSA-N

6: InChI=1S/C12H12/c1-2-4-6-5(11-7(1)10(4)11)3(1)9-8(2)12(6)9/h1-12H
InChIKey=DUDCBTWUEJEMGD-UHFFFAOYSA-N

The role of dispersion in organic chemistry has been slowly recognized as being quite critical in a variety of systems. I have blogged on this subject many times, discussing new methods for properly treating dispersion within quantum computations along with a variety of molecular systems where dispersion plays a critical role. Schreiner¹ has recently published a very nice review of molecular systems where dispersion is a key component towards understanding structure and/or properties.

In a similar vein, Wegner and coworkers have examined the Z to E transition of azobenzene systems (1a-g → 2a-g) using both experiment and computation.² They excited the azobenzenes to the Z conformation and then monitored the rate for conversion to the E conformation. In addition they optimized the geometries of the two conformers and the transition state for their interconversion at both B3LYP/6-311G(d,p) and B3LYP-D3/6-311G(d,p). The optimized structure of the t-butyl-substituted system is shown in Figure 1.

a: R=H; b: R=tBu; c: R=Me; d: R=iPr; e: R=Cyclohexyl; f: R=Adamantyl; g: R=Ph

1b

1b-TS-2b

2b

Figure 1. B3LYP-D3/6-311G(d,p) optimized geometries of 1a, 2a, and the TS connecting them.

The experiment finds that the largest activation barriers are for the adamantly 1f and t-butyl 1b azobenzenes, while the lowest barriers are for the parent 1a and methylated 1c azobenzenes.

The trends in these barriers are not reproduced at B3LYP but are reproduced at B3LYP-D3. This suggests that dispersion is playing a role. In the Z conformations, the two phenyl groups are close together, and if appropriately substituted with bulky substituents, contrary to what might be traditionally thought, the steric bulk does not destabilize the Z form but actually serves to increase the dispersion stabilization between these groups. This leads to a higher barrier for conversion from the Z conformer to the E conformer with increasing steric bulk.

References

(1) Wagner, J. P.; Schreiner, P. R. "London Dispersion in Molecular Chemistry—Reconsidering Steric Effects," Angew. Chem. Int. Ed. 2015, 54, 12274-12296, DOI: 10.1002/anie.201503476.

(2) Schweighauser, L.; Strauss, M. A.; Bellotto, S.; Wegner, H. A. "Attraction or Repulsion? London Dispersion Forces Control Azobenzene Switches," Angew. Chem. Int. Ed. 2015, 54, 13436-13439, DOI: 10.1002/anie.201506126.

InChIs

1b: InChI=1S/C28H42N2/c1-25(2,3)19-13-20(26(4,5)6)16-23(15-19)29-30-24-17-21(27(7,8)9)14-22(18-24)28(10,11)12/h13-18H,1-12H3/b30-29-
InChIKey=SOCNVTNVHBWFKC-FLWNBWAVSA-N

2b: InChI=1S/C28H42N2/c1-25(2,3)19-13-20(26(4,5)6)16-23(15-19)29-30-24-17-21(27(7,8)9)14-22(18-24)28(10,11)12/h13-18H,1-12H3/b30-29+
InChIKey=SOCNVTNVHBWFKC-QVIHXGFCSA-N

Here is another fine example of the power of combining experiment and computation. Xu and co-worker has applied the FT microwave technique, which has been used in conjunction with computation by the Alonso group (especially) as described in these posts, to the trimer of 2-fluoroethanol.¹ They computed a number of trimer structures at MP2/6-311++G(2d,p) in an attempt to match up the computed spectroscopic constants with the experimental constants. The two lowest energy structures are shown in Figure 1. The second lowest energy structure has nice symmetry, but it does not match up well with the experimental spectra. However, the lowest energy structure is in very good agreement with the experiments.

(0.0)

(4.15)

Table 1. MP2/6-311++G(2d,p) optimized structures and relative energies (kJ mol^-1) of the two lowest energy structures of the trimer of 2-fluoroethanol. The added orange lines in the lowest energy structure denote the bifurcated hydrogen bonds identified by QTAIM.

Of particular note is that topological electron density analysis (also known as quantum theoretical atoms in a molecule, QTAIM) of the wavefunction of the lowest energy structure of the trimer identifies two hydrogen bond bifurcations. The authors suggest that these additional interactions are responsible, in part, for the stability of this lowest energy structure.

References

(1) Thomas, J.; Liu, X.; Jäger, W.; Xu, Y. "Unusual H-Bond Topology and Bifurcated H-bonds in the 2-Fluoroethanol Trimer," Angew. Chem. Int. Ed. 2015, 54, 11711-11715, DOI: 10.1002/anie.201505934.

InChIs

2-fluoroethanol: InChI=1S/C2H5FO/c3-1-2-4/h4H,1-2H2, InChIKey=GGDYAKVUZMZKRV-UHFFFAOYSA-N