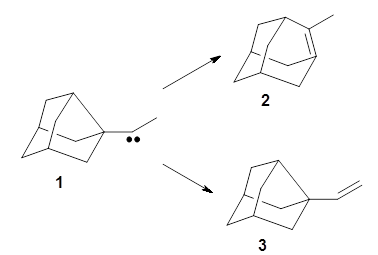
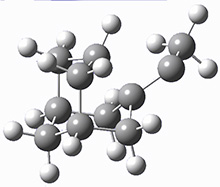
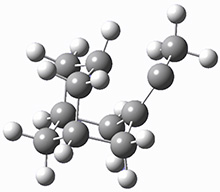
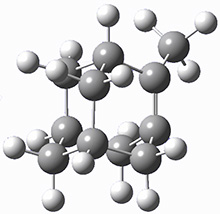
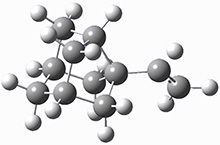
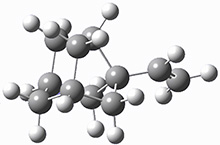
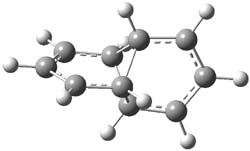
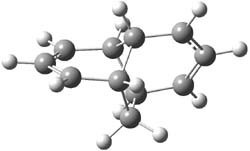
I seem to be recently flooded with papers dealing with tunneling in organic systems. Well, here’s one more! Kozuch, Borden, Schreiner and co-workers seek out systems whereby isotopic substitution might lead to reaction selectivity.¹ Their base system is cyclopropylmethylcarbene 1, which can undergo three different reactions: (a) the ring can expand to give 1-methylcyclobut-1-ene 2, (b) a hydrogen can shift from the terminal methyl group to give vinylcyclopropane 3, or (c) the methane hydrogen can shift to produce ethylidenecyclopropane 4. This last option can be neglected since its barrier (20.5 kcal mol^-1) is so much higher than for the other two, 7.5 kcal mol^-1 for the ring expansion and 12.1 kcal mol^-1 for the [1,2]H-shift converting 1 → 3.

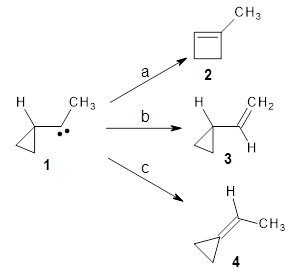
At high temperature, the ring expansion to 2 will dominate, but at low temperature the hydrogen shift to 3 might dominate by tunneling through the barrier due to the low mass and short distances involved. The reaction rates were computed using B3LYP/6-31G(d,p) and small-curvature tunneling. At low temperature, the rate for the hydrogen shift is 10 orders of magnitude faster than the ring expansion. Thinking that deuterium substitution of the terminal methyl group might slow down the rate of the [1,2]-shift, they computed the rates for the reactions of 1-d3, and in fact the rate of this shift does reduce by 10⁴ but it is still much faster than the rate for ring expansion. What is needed is a system where the rate for ring expansion is slower than the rate for hydrogen migration but faster than the rate of deuterium migration.

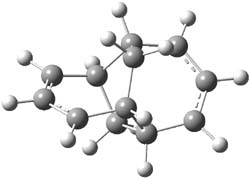
They examine a number of different substituents that may help to lower the barrier for the ring expansion. The methoxy derivative 5 turns out to suit the bill perfectly. The methoxy group reduces the barrier for ring expansion from 7.5 kcal mol^-1 with 1 to 2.5 kcal mol^-1 with 5. With hydrogenated 5, the [1,2]H-shift is 10³ times faster than ring expansion, but with deuterated 5, ring expansion is twice as fast as the deuterium migration.

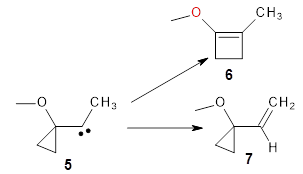
The authors call this isotope controlled selectivity (ICS), and this is the first example of this type of control.

References

1. Nandi, A.; Gerbig, D.; Schreiner, P. R.; Borden, W. T.; Kozuch, S., Isotope-Controlled Selectivity by Quantum Tunneling: Hydrogen Migration versus Ring Expansion in Cyclopropylmethylcarbenes. J. Am. Chem. Soc. 2017, 139, 9097-9099, DOI: 10.1021/jacs.7b04593.

InChIs

1: InChI=1S/C5H8/c1-2-5-3-4-5/h5H,3-4H2,1H3
InChIKey=KJIJNBZLGHBOTI-UHFFFAOYSA-N

2: InChIInChIKey=AVPHQXWAMGTQPF-UHFFFAOYSA-N

3: InChI=1S/C5H8/c1-2-5-3-4-5/h2,5H,1,3-4H2
InChIKey=YIWFBNMYFYINAD-UHFFFAOYSA-N

4: InChI=1S/C5H8/c1-2-5-3-4-5/h2H,3-4H2,1H3
InChIKey=ZIFNDRXSSPCNID-UHFFFAOYSA-N

5: InChI=1S/C6H10O/c1-3-6(7-2)4-5-6/h4-5H2,1-2H3
InChIKey=YMBSTCICUAORNN-UHFFFAOYSA-N

6: InChIInChIKey=QBLNAZHAVPMLHB-UHFFFAOYSA-N

7: InChIInChIKey=FHYLDABSPVPDTJ-UHFFFAOYSA-N

Another prediction made by quantum chemistry has now been confirmed. In 2010, Zhang, Hrovat, and Borden predicted that the degenerate rearrangement of semibullvalene 1 occurs with heavy atom tunneling.¹ For example, the computed rate of the rearrangement including tunneling correction is 1.43 x 10^-3 s^-1 at 40 K, and this rate does not change with decreasing temperature. The predicted half-life of 485 s is 10¹⁰ shorter than that predicted by transition state theory.

Now a group led by Sander has examined the rearrangement of deuterated 2.² The room temperature equilibrium mixture of d⁴–2 and d²–2 was deposited at 3 K. IR observation showed a decrease in signal intensities associated with d⁴–2 and concomitant growth of signals associated with d²–2. The barrier for this interconversion is about 5 kcal mol^-1, too large to be crossed at this temperature. Instead, the interconversion is happening by tunneling through the barrier (with a rate about 10^-4 s^-1), forming the more stable isomer d²–2 preferentially. This is exactly as predicted by theory!

References

1. Zhang, X.; Hrovat, D. A.; Borden, W. T., "Calculations Predict That Carbon Tunneling Allows the Degenerate Cope Rearrangement of Semibullvalene to Occur Rapidly at Cryogenic Temperatures." Org. Letters 2010, 12, 2798-2801, DOI: 10.1021/ol100879t.

2. Schleif, T.; Mieres-Perez, J.; Henkel, S.; Ertelt, M.; Borden, W. T.; Sander, W., "The Cope Rearrangement of 1,5-Dimethylsemibullvalene-2(4)-d1: Experimental Evidence for Heavy-Atom Tunneling." Angew. Chem. Int. Ed. 2017, 56, 10746-10749, DOI: 10.1002/anie.201704787.

InChIs

1: InChI=1S/C8H8/c1-3-6-7-4-2-5(1)8(6)7/h1-8H
InChIKey=VEAPRCKNPMGWCP-UHFFFAOYSA-N

d⁴–2: InChI=1S/C10H12/c1-9-5-3-7-8(4-6-9)10(7,9)2/h3-8H,1-2H3/i5D
InChIKey=WUJOLJNLXLACNA-UICOGKGYSA-N

d²–2: InChI=1S/C10H12/c1-9-5-3-7-8(4-6-9)10(7,9)2/h3-8H,1-2H3/i7D
InChIKey=WUJOLJNLXLACNA-WHRKIXHSSA-N

What is the spin state of the ground state of an aromatic species? Can this be spin state be manipulated by charge? These questions are addressed by Borden, Kim, Sessler and coworkers¹ for the hexaphyrin 1. B3LYP/6-31G(d) optimization of 1 shows it to be a ground state singlet. This structure is shown in Figure 1.

Protonation of the three pyrrole nitrogens creates 1³⁺, which has interesting frontier orbitals. The HOMO of 1³⁺, of a₁” symmetry, has nodes running through all six nitrogens. The next higher energy orbital, of a₂” symmetry, has a small π-contribution on each nitrogen. Protonation will therefore have no effect on the energy of the a₁” orbital, but the charge will stabilize the a₂” orbital. This will lower the energy gap between the two orbitals, suggesting that a ground state triplet might be possible. The lowest singlet and triplet states of 1³⁺ are also shown in Figure 1.

1
Singlet 13+	Triplet 13+

Figure 1. (U)B3LYP/6-31G(d) optimized structures of 1 and singlet and triplet 1³⁺.

This spin state change upon protonation was experimentally verified by synthesis of two analogues of 1, shown below. The triprotonated versions of both are observed to have triplet character in their EPR spectrum.

References

(1) Fukuzumi, S.; Ohkubo, K.; Ishida, M.; Preihs, C.; Chen, B.; Borden, W. T.; Kim, D.; Sessler, J. L. "Formation of Ground State Triplet Diradicals from Annulated Rosarin Derivatives by Triprotonation," J. Am. Chem. Soc. 2015, 137, 9780-9783, DOI: 10.1021/jacs.5b05309.

InChIs

1: InChI=1S/C45H24N6/c1-2-8-29-28(7-1)34-16-22-13-24-18-36-30-9-3-4-10-31(30)38-20-26(50-43(38)42(36)48-24)15-27-21-39-33-12-6-5-11-32(33)37-19-25(49-44(37)45(39)51-27)14-23-17-35(29)41(47-23)40(34)46-22/h1-21,46,49-50H/b22-13-,23-14-,24-13-,25-14-,26-15-,27-15-
InChIKey=UMEHBSBBAUKCTH-UIJINECUSA-N

As recently explicated by Wang and Borden using NIPE spectroscopy and computations, the potential energy surface of cyclopropyl-1,2,3-trione 1 is remarkably complex.¹ (U)CCSD(T)//aug-cc-pVTZ computations of the D_3h singlet (the ¹A_1’ state shown in Figure 1) is actually a hilltop, possessing two imaginary frequencies. Distorting the structure as indicated by these imaginary frequencies and then optimizing the structure leads directly to dissociation to three CO molecules. Thus, (CO)₃ does not exist as a stable minima on the singlet surface.

The D_3h triplet (the ³E” state shown in Figure 1) is not a critical point on the surface; due to the Jahn-Teller effect is distorts into two different states: the ³B₁ state which is a local energy minimum, and the ³A₂ state which is a transition state between the symmetry-related ³B₁ states.

So, this implies the possibility of a very interesting NIPE experiment. If the radical anion (CO)₃^-.
loses an electron and goes to the singlet surface, it lands at a hilltop(!) and should have a very short lifetime. If it goes to the triplet surface, it lands at either a transition state (³A₂) and again should have a short lifetime, or it can land at the ³B₁ state and perhaps have some lifetime before it dissociates by losing one CO molecule.

1-.
1A1’	3E”
3B1	3A2

Figure 1. (U)CCSD(T)//aug-cc-pVTZ optimized geometries of 1 and its radical anion.

The NIPE spectrum identifies three transitions. By comparing the energies of the electron loss seen in the experiment with the computations, along with calculating the Franck-Condon factors using the computed geometries and vibrational frequencies, the lowest energy transition is to the ¹A_1’ state, and the second transition is part of the vibrational progression also to the ¹A_1’ state. This is the first identification of vibrational frequencies associated with a hilltop structure. The third transition is to the ³A₂ state. No transition to the ³B₁ state is found due to the large geometric difference between the radical anion and the ³B₁ state; the Franck-Condon factors are zero due to no overlap of their wavefunctions.

Once again, the power of the symbiotic relationship between experiment and computation is amply demonstrated in this paper.

References

(1) Chen, B.; Hrovat, D. A.; West, R.; Deng, S. H. M.; Wang, X.-B.; Borden, W. T. "The Negative Ion Photoelectron Spectrum of Cyclopropane-1,2,3-Trione Radical Anion, (CO)₃^•– — A Joint Experimental and Computational Study," J. Am. Chem. Soc. 2014, 136, 12345-12354, DOI: 10.1021/ja505582k.

InChIs

1: InChI=1S/C3O3/c4-1-2(5)3(1)6
InChIKey=RONYDRNIQQTADL-UHFFFAOYSA-N

The notion of tunneling control has been a topic of interest within this blog a number of times. As developed by Schreiner and Allen,^1,2 tunneling control is a third means for predicting (or directing) the outcome of a reaction, alongside the more traditionally recognized kinetic and thermodynamic control. Tunneling control occurs when tunneling through a higher barrier is preferred over tunneling through a lower barrier.

Kozuch and Borden propose another example of tunneling control, this time in the rearrangement of the noradamantyl carbene 1.³ This carbene can undergo a 1,2-carbon shift, driven by strain relief to form the alkene 2. The alternative as a 1,2-hydrogen shift that produces the alkene 3.

These two reaction pathways were explored using B3LYP/6-31G(d,p) computations coupled with canonical variational theory and small curvature tunneling corrections. Structures of the reactant 1 and the two transition states leading to the two products 2 and 3 are shown in Figure 1. The activation barrier at 300 K is 5.4 kcal mol^-1 leading to 2 and 8.6 kcal mol^-1 leading to 3. Tunneling is expected to be much more important for the hydrogen shift than for the carbon shift, but even including tunneling, the rate to form 2 is much faster than the rate to form 3 at 300 K.

1	TS 1→2	2
	TS 1→3	3

Figure 1. B3LYP/6 optimized structures of 1-3 and the transition states leading to 2 and 3.

The situation is reversed however at cryogenic temperatures (< 20 K). Tunneling is now the only route for the reactions to occur, and the rate for formation of 3 is dramatically greater than the rate of formation of 2, which is inhibited by the movement of the much heavier carbon atom. Perdeuteration of the methyl group of 1, which drastically slows the rate of tunneling in the path to 3, nonetheless still favors this pathway (forming d₃–3) over formation of d₃–2. Thus, at low temperatures the formation of 3 is the preferred product, a manifestation of tunneling control.

Kozuch and Borden end their paper with a hope that an experimentalist will examine this interesting case. I concur!

References

(1) Schreiner, P. R.; Reisenauer, H. P.; Ley, D.; Gerbig, D.; Wu, C.-H.; Allen, W. D. "Methylhydroxycarbene: Tunneling Control of a Chemical Reaction," Science 2011, 332, 1300-1303, DOI: 10.1126/science.1203761.

(2) Ley, D.; Gerbig, D.; Schreiner, P. R. "Tunnelling control of chemical reactions – the organic chemist’s perspective," Org. Biomol. Chem. 2012, 10, 3781-3790, DOI: 10.1039/C2OB07170C.

(3) Kozuch, S.; Zhang, X.; Hrovat, D. A.; Borden, W. T. "Calculations on Tunneling in the Reactions of Noradamantyl Carbenes," J. Am. Chem. Soc. 2013, 135, 17274-17277, DOI: 10.1021/ja409176u.

InChIs

1: InChI=1S/C11H16/c1-2-11-6-8-3-9(7-11)5-10(11)4-8/h8-10H,3-7H2,1H3
InChIKey=CXFJINASYYTBBV-UHFFFAOYSA-N

2: InChI=1S/C11H16/c1-7-10-3-8-2-9(5-10)6-11(7)4-8/h8-10H,2-6H2,1H3
InChIKey=XDANPUSLLJWVEK-UHFFFAOYSA-N

3: InChI=1S/C11H16/c1-2-11-6-8-3-9(7-11)5-10(11)4-8/h2,8-10H,1,3-7H2
InChIKey=JHEPVTWREMDEMG-UHFFFAOYSA-N

The singlet and triplet carbene is the topic of Chapter 4, especially sections 1 and 2. The ground state of methylene is the triplet, with one electron in the σ-orbital and one electron in the π-orbital, with the spins aligned. The lowest singlet state places the pair of electrons in the σ-orbital, and this state is about 9 kcal mol^-1 higher in energy than the triplet. The next lowest singlet state has one electron in each of the σ- and π-orbitals, with the spins aligned. The singlet state with both electrons in the π-orbital is the highest of these four states, some 60 kcal mol^-1 above the ground state triplet.

Hoffmann and Borden now pose the question “Can the doubly occupied π carbene (¹A₁-σ⁰π²) be the ground state with appropriate substitution?” The answer they find is yes!¹

The trick is to find a combination of substituents that will raise the energy of the σ-orbital and lower the energy of the π-orbital. The latter effect can be enhanced if the π-orbital can be a part of an aromatic (6e^–) ring.

Two of the best possibilities for identifying a ground state ¹A₁-σ⁰π² carbene are 1 and 2. The CASSCF/6-31G(d) optimized geometries of these two are shown in Figure 1. In 1, the nitrogen lone pairs act to destabilize the σ-orbital, while the aldehyde group acts as a withdrawing group to stabilize the π-orbital. The result is that the ¹A₁-σ⁰π⁶ state of 1 is predicted to be about 8 kcal mol^-1 more stable than the triplet state, as per CASPT2 and CCSD(T) computations.

An ever greater effect is predicted for 2. Here the nitrogen lone pairs adjacent to the carbene act to destabilize the σ-orbital. The empty π-orbital on B lowers the energy of the carbene π-orbital by making it part of the 6-electron aromatic ring. The ¹A₁-σ⁰π⁶ state of 2 is predicted to be about 25 kcal mol^-1 more stable than its triplet state!

1

2

Figure 1. CASSCF/6-31G(d) optimized geometries of the ¹A₁-σ⁰π⁶ states of 1 and 2.

References

(1) Chen, B.; Rogachev, A. Y.; Hrovat, D. A.; Hoffmann, R.; Borden, W. T. "How to
Make the σ⁰π² Singlet the Ground State of Carbenes," J. Am. Chem. Soc. 2013, 135, 13954-13964, DOI: 10.1021/ja407116e.

InChIs

1: InChI=1S/C5H2N2O2/c8-1-4-5(2-9)7-3-6-4/h1-2H
InChIKey=QDSVROXEBBWIOO-UHFFFAOYSA-N

2: InChI=1S/C3H3BN2/c1-4-2-6-3-5-1/h1-2,4H
InChIKey=MQJXDZBYOSOLST-UHFFFAOYSA-N

Interacting bis-allyl radicals are the topic of a computational study by Gleiter and Borden.¹ The new twist is to have the two allyl groups interact through a cyclobutyl, cyclopentyl or cyclohexyl ring, as in 1-3.

The degree of interaction of the radical electrons is evaluated with a number of metrics. First, the singlet-triplet energy gap is computed at CASSCF(6,6)/6-31G(d) and UB3LYP/6-31G(d). A larger gap is suggestive of strong interaction between the two allyl radicals. Next, the <S²> value of the UB3LYP wavefunction will be 0 for a pure singlet, which occurs when the radicals are strongly interacting. A value near 1 suggests an electron localized into each allyl fragment. Lastly, the natural orbital occupation numbers (NOON) of the two highest lying orbitals would be 2 and 0 for the pure interacting state and each would be 1 for the non-interacting state. The B3LYP/6-31G(d) optimized geometries of 1-3 are shown in Figure 1. The values of each metric are listed in Table 1.

1	2
3

Figure 1. B3LYP/6-31G(d) optimized geometries of 1-3.

Table 1. Metrics for evaluating the allyl interaction in 1-3.

The different metrics are all consistent. The allyl radicals are strongly interacting in 1, with a low lying singlet state. The interaction is significantly lessened in 2 and smaller still in 3. The authors argue these differences in terms of the molecular orbital interactions between the allyl fragments and the central ring fragment.

References

(1) Lovitt, C. F.; Dong, H.; Hrovat, D. A.; Gleiter, R.; Borden, W. T., "Through-Bond Interactions in the Diradical Intermediates Formed in the Rearrangements of Bicyclo[n.m.0]alkatetraenes," J. Am. Chem. Soc., 2010, 132, 14617-14624, DOI: ja106329t

InChIs

1: InChI=1/C10H10/c1-3-7-9-5-2-6-10(7)8(9)4-1/h1-10H
InChIKey=QQZALYREQJSRLB-UHFFFAOYAA

2: InChI=1/C11H12/c1-3-8-7-9-4-2-6-11(8)10(9)5-1/h1-6,8-11H,7H2
InChIKey=XHSRXRHTBHVJQX-UHFFFAOYAV

3: InChI=1/C12H14/c1-3-9-7-12-6-2-5-11(9)8-10(12)4-1/h1-6,9-12H,7-8H2
InChIKey=JFNCWTOWDGQJLS-UHFFFAOYAA

Borden predicted measurable heavy-atom isotope effects in the ring opening of cyclopropylcarbinyl radical. In my blog post on this paper, I concluded with the line:

Borden hopes that experimentalists will reinvestigate this
problem (and hopefully confirm his predictions).

Well, in a recent paper where Borden collaborates with Singleton, these predictions are confirmed!¹

There is a sizable kinetic isotope effect for breaking the ring bond to a ¹²C over a bond to a ¹³C atom, up to 16% at -100 °C. The KIE predicted without including tunneling are dramatically below the experimental values, but incorporation of tunneling in the computated KIEs match up with experiment with an error no greater that 0.7%. The Arrhenius plot of ln KIE vs. 1/T shows enhanced isotope effects when tunneling is included, very nice agreement between the experimental and tunneling-corrected KIEs and curvature – all indicative of heavy atom tunneling. Lastly, the ring open product (1-butene) is the observed major product (62%) at -100 °C; the minor product is methylcyclopropane. In the absence of heavy-atom tunneling, 1-butene would be the minor product (28%).

References

(1) Gonzalez-James, O. M.; Zhang, X.; Datta, A.; Hrovat, D. A.; Borden, W. T.; Singleton, D. A. J. Am. Chem. Soc., 2010, 132, 12548-12549, DOI: 10.1021/ja1055593.

InChIs

Cyclopropylcarbonyl radical: InChI=1/C4H7/c1-4-2-3-4/h4H,1-3H2
InChIKey=RMCDUNHIVVEEDD-UHFFFAOYAR

1-butene: InChI=1/C4H8/c1-3-4-2/h3H,1,4H2,2H3
InChIKey=VXNZUUAINFGPBY-UHFFFAOYAZ

Following up on his previous studies of isotope effects on the ring opening of cyclopropylcarbinyl radical 1 to give 2 (see my previous post), Borden now reports on its kinetic isotope effect (KIE).¹

Using the small-curvature tunneling approximation along with structures and frequencies computed at B3LYP/6-31G(d), he finds a negligible KIE at C₁, consistent with little motion of C₁ in the transition vector. The KIE for substitution at C₄ is large (k(¹²C/¹⁴C)=5.46), also consistent with its large motion in the transition vector. What is surprising is the KIE for deuterium substitution at C₁: 0.37. This is a large inverse isotope effect!

Analysis of the vibrational frequencies that involve the C₁ hydrogens provides an explanation. In going to the TS for the ring opening, both the torsional motion about the C₁-C₂ bond (making the double bond) and the pyramidal motion increase in frequency. This leads to a higher activation barrier for H than D, and the inverse isotope effect.

References

(1) Zhang, X.; Datta, A.; Hrovat, D. A.; Borden, W. T., “Calculations Predict a Large Inverse H/D Kinetic Isotope Effect on the Rate of Tunneling in the Ring Opening of Cyclopropylcarbinyl Radical,” J. Am. Chem. Soc., 2009, 131, 16002-16003, DOI: 10.1021/ja907406q.

The longstanding unknown oxyallyl diradical (1) singlet-triplet gap has now been addressed with a very nice photoelectron spectroscopy study by Lineberger with interpretation greatly aided by computations provided by Hrovat and Borden.¹

The photoelectron detachment spectrum of oxyallyl radical anion shows 5 major peaks, one at 1.942 eV and a series of four peaks starting at 1.997 eV separated by 405 cm^-1.

B3LYP/6-311++G(d,p) computations indicate that the energy for electron detachment from the radical anion to triplet oxyallyl diradical is 1.979 eV. (The structure of triplet 1 is shown in Figure 1.) Further, the computed vibrational frequency of the C-C-C bend is 408 cm^-1. These computations suggest that the four peak sequence represents a vibrational progression in the C-C-C bend of the triplet oxyallyl diradical.

1A1

3B2

Figure 1. Structures of the singlet and triplet oxyallyl diradical 1.¹

CASPT2 computations on singlet oxyallayl diradical indicate that it lies in a very shallow well, lower than the zero-point energy. (This structure is shown in Figure 1.) In fact, the singlet diradical can collapse without a barrier to cyclopropanone. Interestingly, the C-O stretching frequency of 1 is computed to be 1731 cm^-1, and close inspection of the photoelectron spectrum does show a progression of this magnitude originating from peak A. Therefore, both the singlet and triplet states of 1 are identified and their gap is extraordinarily small – the singlet is only 0.055 eV lower in energy than the triplet.

References

(1) Ichino, T.; Villano, S. M.; Gianola, A. J.; Goebbert, D. J.; Velarde, L.; Sanov, A.; Blanksby, S. J.; Zhou, X.; Hrovat, D. A.; Borden, W. T.; Lineberger, W. C., "The Lowest Singlet and Triplet States of the Oxyallyl Diradical," Angew. Chem. Int. Ed., 2009, 48, 8509-8511, DOI: 10.1002/anie.200904417