Palau’amine has been of interest since its discovery in the early 1990s. It was just recently synthesized by Baran,¹ to much acclaim. The structure of palau’amine underwent numerous revisions, and though the relative configuration had been settled, the absolute configuration was only determined by Reinscheid and Griesinger using a combination of experimental and computed ECD and ORD spectra.²

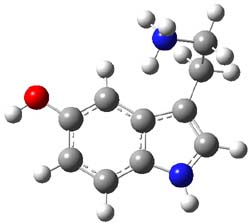
3,4-dibromopalau’amine 1 was subjected to careful NMR analysis to set as much of the overall structure as possible. Then two conformations were optimized at B3LYP/6-31G(d), one of which is displayed in Figure 1.

1

Figure 1. B3LYP/6-31G(d) optimized structure of 1.

TD-DFT computations including PCM gave an ECD spectrum that nicely matches with experiment, especially where the positive and negative peaks occur. The computed and experimental ORD spectra also match well, with all the signs matching up and a difference in the absolute value of the rotation of no more that 25%. The resulting absolute configuration is (-)-(6S,10R,11S,12S,16R,17S,18S,20S)-dibromopalau’amine, demonstrating again the power of combining computation and experiment for structure determination!

References

(1) Seiple, I. B.; Su, S.; Young, I. S.; Lewis, C. A.; Yamaguchi, J.; Baran, P. S., "Total Synthesis of Palau’amine," Angew. Chem. Int. Ed., 2010, 49, 1095-1098, DOI: 10.1002/anie.200907112

(2) Reinscheid, U. M.; Köck, M.; Cychon, C.; Schmidts, V.; Thiele, C. M.; Griesinger, C., "The Absolute Configuration of Dibromopalau’amine," Eur. J. Org. Chem., 2010, 6900-6903, DOI: 10.1002/ejoc.201001392

InChI

1: InChI=1/C17H22Br2ClN9O2/c18-6-1-7-11(30)28-3-5-4(2-21)9(20)16(13(31)25-15(23)26-16)8(5)17(28)12(24-14(22)27-17)29(7)10(6)19/h1,4-5,8-9,12-13,24-27,31H,2-3,21-23H2/q+2/p+1/t4-,5-,8+,9+,12+,13+,16+,17-/m1/s1/fC17H23Br2ClN9O2/h21H/q+3
InChIKey=VGQTUXLYZXIYTJ-CAGSSHLPDN

1,2-Azaborine appears to be aromatic (see my previous post). Can the extent of aromatic character be measured? Well, obviously the first thing one must decide is just which “aromaticity metric” to choose. Dixon and Liu have now measured the aromatic resonance stablilization energy (ASE) through computations and heats of hydrogenation.¹

One can set up to hydrogenation comparisons. First, obtain the hydrogenation of 1,2-azaborine itself. They used the t-butyl analog 1, so the hydrogenation is given in Reaction 1.

Then as comparison, one can perform two separate hydrogenations, looking at the double bond adjacent to the nitrogen (Reaction 2) and the double bond adjacent to the boron (Reaction 3).

The heat of hydrogenation of Reaction 1 is -30 ± 1 kcal mol^-1 (-30.1 at G3(MP2). The heats of hydrogenations of reactions 2 and 3 are -22.7 ± 0.5 kcal mol^-1 (-23.8) and -23.9 ± 0.7 (-24.7), respectively. The difference between the sum of reactions 2 and 3 and Reaction 1 is the ASE: 16.6 kcal mol^-1 (18.4 at G3(MP2)). This can be compared to the ASE of benzene determined in the analogous way to be 32.4 kcal mol^-1. Therefore, 1,2-azoborine is aromatic, but appreciably less so than benzene, which is consistent with the NICS computations (see the post).

References

(1) Campbell, P. G.; Abbey, E. R.; Neiner, D.; Grant, D. J.; Dixon, D. A.; Liu, S.-Y., "Resonance Stabilization Energy of 1,2-Azaborines: A Quantitative Experimental Study by Reaction Calorimetry," J. Am. Chem. Soc., 2010, 132, 18048-18050, DOI: 10.1021/ja109596m

The structure of organic molecules of biochemical significance remains an important pursuit, one that I have discussed in a number of blog posts. Highlighted particularly in this blog (and in my book) has been the interplay of experiment and computation in structure determination. Dopfer and co-workers combine IR multiple photon dissociation (IRMPD) with DFT and MP2 computations to determine the structure of protonated serotonin 1H+.¹

B3LYP/cc-pVDZ and MP2/cc-pVDZ computations of the conformations of 1H+ give nearly identical results. The lowest energy conformer (see Figure 1) has the ethylamine group in a gauche arrangement so that the protonated amine can interact with the π-system of the ring. The hydroxyl group is orientated trans relative to the ethylamine group. Conformer generated by rotation about the C-O bond or the C-C and C-N bond of the ethylamine group are higher in energy, anywhere from 0.5 to about 5 kcal mol^-1 above the lowest conformer. Protonation at the ring nitrogen or the oxygen are more than 20 kcal mol^-1 higher in energy than the lowest conformer.

1H+

Figure 1. B3LYP/6-31G(d) optimized geometry of 1H+. Note that the authors did not supply sufficient information in their supporting materials to generate the full 3-D coordinates of the molecule, and I did not want to reoptimize at cc-pVDZ. Referees – please insist on complete supporting information!

Comparison of the experimental IR spectrum of 1H+ with the computed IR frequencies (either B3LYP or MP2 – they are very similar) reveals a remarkable agreement with the computed spectra of just the lowest energy conformer. While the lowest energy conformer is predicted to be nearly 70% of the population, there is little spectroscopic evidence of the participation of any other conformer. In fact, the next three lowest energy conformers have a distinctive peak (in their computed IR spectrum) at about 1400 cm^-1, a region that has virtually no absorption in the experimental IR.

References

(1) Lagutschenkov, A.; Langer, J.; Berden, G.; Oomens, J.; Dopfer, O., "Infrared Spectra of Protonated Neurotransmitters: Serotonin," J. Phys. Chem. A, 2010, 114, 13268-13276, DOI: 10.1021/jp109337a

InChIs

serotonin: InChI=1/C10H12N2O/c11-4-3-7-6-12-10-2-1-8(13)5-9(7)10/h1-2,5-6,12-13H,3-4,11H2
InChIKey=QZAYGJVTTNCVMB-UHFFFAOYAX

1H+: InChI=1/C10H12N2O/c11-4-3-7-6-12-10-2-1-8(13)5-9(7)10/h1-2,5-6,12-13H,3-4,11H2/p+1/fC10H13N2O/h11H/q+1
InChIKey=QZAYGJVTTNCVMB-HISXSYJOCA

This one is a bit afield from organic chemistry, but the result is important for computational chemists who are interested in electron density analysis.

The topological electron density analysis of Bader (also called Atoms-In-Molecules – AIM) carves up a molecular electron density into regions associated with an attractor. The attractor is a critical point in the electron density that is a maximum in all directions. Gradient paths, paths that trace increasing electron density, terminate at such an attractor. The union of all such paths defines a basin. Bader found that for typical molecules, the attractor is coincident with the position of the atomic nucleus. He has then assumed a 1:1 correspondence between these two – all nuclei are attractors and all attractors correspond with nuclei.

This correspondence has been questioned in computations on some metals. For example, Li_n and Na_n (n=2,4,6) have a non-nuclear attractor. However, no clear-cut unambiguous experimental observation of non-nuclear attractors has been made, until now. Platts and Stasch¹ have obtained the x-ray diffraction electron density of 1 and they find a non-nuclear attractor near the midpoint of the Mg-Mg bond. This is corroborated by DFT computations of 1 and some related systems. It should be said that the electron density along the Mg-Mg path is quite flat in the middle, but the attractor is present, and the integrated number of electrons within the basin associated with this non-nuclear attractor is a non-trivial 0.81 e (experiment) or 0.79 e (DFT).

It now appears incontrovertible that non-nuclear attractors of the molecular electron density can exist. It would be especially interesting if these types of points could be located in organic species.

References

(1) Platts, J. A.; Overgaard, J.; Jones, C.; Iversen, B. B.; Stasch, A., "First Experimental Characterization of a Non-nuclear Attractor in a Dimeric Magnesium(I) Compound," J. Phys. Chem. A, 2011, 115, 194-200, DOI: 10.1021/jp109547w