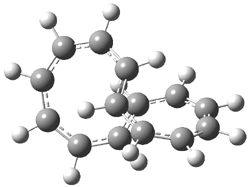
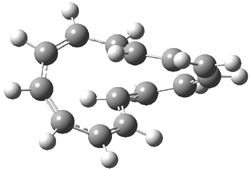
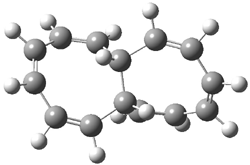
Rzepa has published another study of Möbius aromaticity.¹ Here he examines the [14]annulene 1 using the topological method (AIM) and NICS. The B3LYP/6-31G(d) optimized structures of 1, the transition state 3 and product of the 8-e^– electroclization 2 are shown in Figure 1.

1 (0.0)

3 (4.56)

2 (0.07)

Figure 1. B3LYP/6-31G(d) optimized structures and relative energies (kcal mol^-1) of 1-3.¹

The topological analysis of 1 reveals a number of interesting features of the density. First, there are two bond critical points that connect the carbon atoms that cross over each other in the lemniscate structure 1 (these bond paths are drawn as the dashed lines in Scheme 1, connecting C₁ to C₈ and C₇ to C₁₄). These bond critical points have a much smaller electron density than for a typical C-C bond. With these added bond critical points come additional ring points, but not the anticipated 3 ring critical points. There is a ring critical point for the quasi-four member ring (C₁-C₁₄-C₇-C₈-C₁), but the expected ring point for each of the two 8-member ring bifurcate into two separate ring critical points sandwiching a cage critical point!

Scheme 1

Rzepa argues that the weak bonding interaction across the lemniscates is evidence for Möbius homoaromaticity in each half of 1. The NICS value at the central ring critical point is -18.6 ppm, reflective of overall Möbius aromaticity. But the NICS values at the 8-member ring ring critical points of -8.6 ppm and the cage critical points (-7.9 ppm) provide support for the Möbius homoaromaticity.

Transition state 3 corresponds to motion along the bond path of those weak bonds along either C₁-C₈ or C₇-C₁₄. This leads to forming the two fused eight-member rings of 2. An interesting thing to note is that there is only one transition state connecting 1 and 2 – even though one might think of the electrocyclization occurring in either the left or right ring. (Rzepa discusses this in a nice J. Chem. Ed. article.²) This transition state 3 is stabilized by Möbius aromaticity.

As an aside, Rzepa has once again made great use of the web in supplying a great deal of information through the web-enhanced object in the paper. As in the past, ACS continues to put this behind the subscriber firewall instead of considering it to be supporting material, which it most certainly is and should therefore be available to all.

References

(1) Allan, C. S. M.; Rzepa, H. S., "Chiral Aromaticities. AIM and ELF Critical Point and NICS Magnetic Analyses of Moöbius-Type Aromaticity and Homoaromaticity in Lemniscular Annulenes and Hexaphyrins," J. Org. Chem., 2008, 73, 6615-6622, DOI: 10.1021/jo801022b.

(2) Rzepa, H. S., "The Aromaticity of Pericyclic Reaction Transition States" J. Chem. Ed. 2007, 84, 1535-1540, http://www.jce.divched.org/Journal/Issues/2007/Sep/abs1535.html.

InChIs

1:
InChI=1/C14H14/c1-2-4-6-8-10-12-14-13-11-9-7-5-3-1/h1-14H/b2-1-,3-1-,4-2-,5-3-,6-4-,7-5+,8-6+,9-7-,10-8+,11-9-,12-10+,13-11-,14-12-,14-13-
InChIKey= RYQWRHUSMUEYST-YGYPEFQEBU

2: InChI=1/C14H14/c1-2-6-10-14-12-8-4-3-7-11-13(14)9-5-1/h1-14H/b2-1-,4-3-,9-5-,10-6-,11-7-,12-8-/t13-,14+
InChIKey= AMYHCQKNURYOBO-RFCQUTFOBS

Cramer and Truhlar have tested their latest solvation model SM8 against a test set of 17 small, drug-like molecules.¹ Their best result comes with the use of SM8, the MO5-2X functional, the 6-31G(d) basis set and CM4M charge model. This computational model yields a root mean squared error for the solvation free energy of 1.08 kcal mol^-1 across this test set. This is the first time these authors have recommended a particular computational model. Another interesting point is that use of solution-phase optimized geometries instead of gas-phase geometries leads to only marginally improved solvation energies, so that the more cost effective use of gas-phase structures is encouraged.

These authors note in conclusion that further improvement of solvation prediction rests upon “an infusion of new experimental data for molecules characterized by high degrees of functionality (i.e. druglike)”.

References

(1) Chamberlin, A. C.; Cramer, C. J.; Truhlar, D. G., “Performance of SM8 on a Test To Predict Small-Molecule Solvation Free Energies,” J. Phys. Chem. B, 2008, 112, 8651-8655, DOI: 10.1021/jp8028038.

Just how difficult can it be to compute rotational barriers? Well, it turns out that for biphenyl 1, the answer is “very”!

The experimental barriers for rotation about the C₁-C_1’ bond of biphenyl are 6.0 ± 2.1 kcal mol^-1 at 0° and 6.5 ± 2.0 kJ mol^-1 at 90°.¹ CCSD(T) with extrapolated basis set approximation computations by Sancho-Garcı´a and Cornil overestimate both barriers by more than 4 kJ mol^-1 and, more critically in error, predict that the 0° barrier is higher in energy than the 90° barrier.²

Now Johansson and Olsen have reported a comprehensive study of the rotational barrier of biphenyl.³ They tackled a number of different effects:

1. Basis sets: The cc-pVDZ basis set is simply too small to give any reasonable estimate (See Table 1).
2. Correlation effects: HF, MP2, SCS-MP2 and CCSD overestimate the barriers and get the relative energies of the two barriers wrong, regardless of the basis set. While CCSD(T) does properly predict the barrier at 0° is lower than that at 90°, even this level overestimates the barrier heights (Table 1).

Table 1. Computed torsional barriers in kJ mol^-1.

	MP2		CCSD(T)
	0°	90°	0°	90°
cc-pVDZ	12.23	7.68	10.89	7.23
aug-cc-pVDZ	9.68	7.45	9.23	6.67
cc-pVTZ	9.86	9.13	8.85	8.50
aug-cc-pVTZ	9.78	9.43	8.83	8.86
cc-pVQZ	9.65	9.33	8.68	8.74
aug-cc-pVQZ	9.35	9.31	8.39	8.76

3. Their best CCSD(T) energy using a procedure to extrapolate to infinite basis set still gives barriers that are too high, though in the right relative order: E(0°)=7.97 and E(90°) = 8.79 kJ mol^-1.
4. Inclusion of Core-Core and Core-Valence correlation energy reduces the 0° barrier and raises the 90° barrier a small amount. With an extrapolation for completeness in the coupled clusters expansion, their best estimates for the two barriers are 7.88 and 8.94 for the 0° and 90° barriers, respectively.
5. Relativity has no effect on the barrier heights. (This is a great result – it suggests that we don’t have to worry about relativistic corrections for normal organics!)
6. Intramolecular basis set superposition error might be responsible for as much a 0.4 kJ difference in the energies of the two barriers.
7. Inclusion of vibrational energies along with all of the other corrections listed above leads to their best estimate of the two barriers: E(0°)=8.0 and E(90°) = 8.3 kJ mol^-1, which are at least in the correct order and within the experimental error bars.

Who would have thought this problem was so difficult?

References

(1) Bastiansen, O.; Samdal, S., "Structure and barrier of internal rotation of biphenyl derivatives in the gaseous state: Part 4. Barrier of internal rotation in biphenyl, perdeuterated biphenyl and seven non-ortho-substituted halogen derivatives," J. Mol. Struct., 1985, 128, 115-125, DOI: 10.1016/0022-2860(85)85044-4.

(2) Sancho-Garcia, J. C.; Cornil, J., "Anchoring the Torsional Potential of Biphenyl at the ab Initio Level: The Role of Basis Set versus Correlation Effects," J. Chem. Theory Comput., 2005, 1, 581-589, DOI: 10.1021/ct0500242.

(3) Johansson, M. P.; Olsen, J., "Torsional Barriers and Equilibrium Angle of Biphenyl: Reconciling Theory with Experiment," J. Chem. Theory Comput., 2008, 4, 1460-1471, DOI: 10.1021/ct800182e.

InChIs

Biphenyl 1: InChI=1/C12H10/c1-3-7-11(8-4-1)12-9-5-2-6-10-12/h1-10H
InChIKey: ZUOUZKKEUPVFJK-UHFFFAOYAV

Following on the great study of hydroxycarbene¹ (see my blog post), Schreiner now reports on the synthesis and characterization of dihydroxycarbene 1.² It is prepared by high-vacuum flash pyrolysis of oxalic acid (Scheme 1).

Scheme 1

Dihydroxycarbene can exist in three different conformations characterized by the relationship about the C-O bond, either s-cis or s-trans. The three conformations are shown in Figure 1, and the s-trans,s-trans structure is the local energy minimum (computed at CCSD(T)/cc-pVTZ).

1tt (0.0)

1ct (0.1)

1cc (6.7)

Figure 1. CCSD(T)/cc-pVTZ optimized geometries and relative energies (kcal mol^-1) of the conformers of 1.²

Identification of the 1 is made through comparison of the experimental and computed IR vibrational frequencies. As an example, the experimental and computed frequencies for the s-trans,s-trans conformer are listed in Table 1. The agreement is excellent.

Table 1. Computed and experimental vibrational frequencies (cm^-1) and intensities (in parentheses) of the s-trans,s-trans conformation of 1.²

Unlike hydroxycarbene, dihydroxycarbene is stable. The amazing instability of hydroxycarbene is due to tunneling through a large barrier: nearly 30 kcal mol^-1.¹ The tunneling route for the decomposition of 1 is more difficult for two reasons. First, its C-O bond is quite strong; the C-O distance is quite short, 1.325 Å. This makes a long distance that must be traversed in the tunneling mode. (The strong bond is due to π-donation from the oxygen lone pair into the empty carbon p orbital; this is noted by the large rotational barrier about the C-O bonds of 17 kcal mol^-1!) Second, the activation barrier for decomposition is very high, at least 34 kcal mol^-1.

References

(1) Schreiner, P. R.; Reisenauer, H. P.; Pickard Iv, F. C.; Simmonett, A. C.; Allen, W. D.; Matyus, E.; Csaszar, A. G., "Capture of hydroxymethylene and its fast disappearance through tunnelling," Nature, 2008, 453, 906-909, DOI: 10.1038/nature07010.

(2) Schreiner, P. R.; Reisenauer, H. P., "Spectroscopic Identification of Dihydroxycarbene13," Angew. Chem. Int. Ed., 2008, 47, 7071-7074, DOI: 10.1002/anie.200802105

InChIs

1: InChI=1/CH2O2/c2-1-3/h2-3H