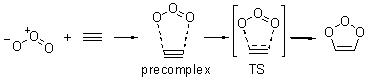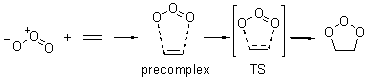The composite methods (exemplified by the Gaussian-n methods, the Weizmann-n methods and CNS-Q methods) are popularly held to be perhaps the best (if not the most straightforward and mechanical) procedures for obtaining accurate energetics. Errors are generally thought to be in the 1-2 kcal mol^-1 range – quite suitable for comparisons with experiment. The recent study of the 1,3-dipolar cycloaddition of ozone with ethene or ethyne offers serious food for thought about considering these composite methods as simple “black-box” solutions towards obtaining good results.
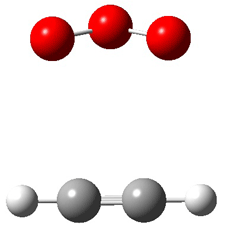
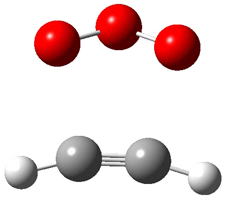
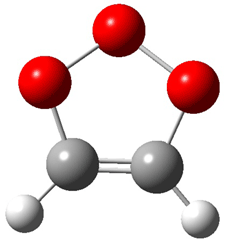
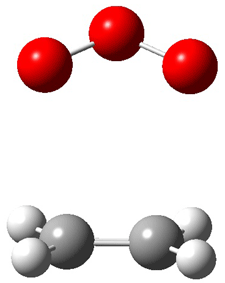
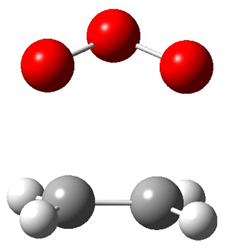
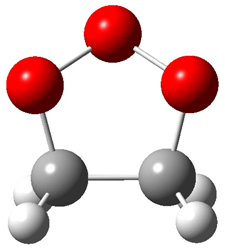
Wheeler, Ess, and Houk have examined the cycloaddition of ozone with ethyne (Reaction 1) and ethane (Reaction 2) with a variety of different computational techniques.¹ Shown in Figure 1 are the CCSD(T)/cc-pVTZ optimized geometries of the pre-complex, transition state and product for both reactions. One of the potential challenges of these reactions is that ozone has appreciable radical character which is also likely to be true in the pre-complex and transition state but the product should have little to no radical character.

	Reaction 1
	Reaction 2

Reaction 1
Precomplex	TS	Product
Reaction 2
Precomplex	TS	Product

The relative enthalphies (0K) of the complex, TS and product were computed using a number of different composite methods. The CBS-QB3, G3, G3B3, G3MP2B3 and G4^2,3 results are listed in Table 1 for both reactions. All of these methods claim a small error – perhaps 1-2 kcal mol^-1. The Gaussian-n methods nicely cluster for the reaction energy for both reactions, while CBS-QB3 predicts both reactions are more exothermic. (The same is also true of CBS-APNO.) The G-n methods indicate that the precomplex is essentially unbound. More concerning is the spread in the enthalpy values of the reaction barrier: the G-n methods predict a barrier that ranges over 5 kcal mol^-1.

Table 1. Relative enthalpies (kcal mol^-1) of the critical points for Reactions 1 and 2.¹

	Reaction 1			Reaction 2
	precomplex	TS	product	precomplex	TS	product
CBS-QB3	-1.2	4.4	-60.8	-0.6	0.7	-54.2
G3	0.3	12.7	-57.7	1.6	0.5	-50.6
G3B3	-0.8	7.8	-57.3	0.0	3.0	-50.8
G3MP2B3	-0.7	7.3	-57.3	0.2	3.0	-50.3
G4	-0.8	9.0	-57.4	-0.3	4.6	-50.4
Focal point	-1.1	9.4	-57.9	-1.2	5.3	-50.9

So what is the correct barrier height? A focal point extrapolation procedure was then performed. This seeks to extrapolate to infinite basis set and estimate the effects of correlation through CCSDT(Q) and includes corrections for the Born-Oppenheimer approximation and special relativistic effects. The focal point results are also shown in Table 1. The new G4 composite method gives enthalpies in very nice agreement with those obtained with the much more expensive focal point procedure. However, the other composite methods fair much worse, especially for the activation barrier.
The convergence of the focal point method for the reaction energy is slow, leading to a large error bar of 2 kcal mol^-1. This appears to relate to the radical character difference between the reactant and product. The convergence for the activation barrier is much better (an error of only 0.2 kcal mol^-1) and here the comparison is between reactant and TS which have similar radical character.
Perhaps the most discouraging aspect of this study is that the relative energy predicted using the highest computational component of the composite method – so, CCSD(T)/6-31+G* for the CBS-QB3 method and QCISD(T)/6-31G(d) for the G3 methods – are more accurate than the composite method itself. But, the reasonable performance of the new G4 method^2,3 does offer some glimmer of hope here.

References

(1) Wheeler, S. E.; Ess, D. H.; Houk, K. N., "Thinking
Out of the Black Box: Accurate Barrier Heights of 1,3-Dipolar Cycloadditions of Ozone with Acetylene and Ethylene," J. Phys. Chem. A, 2008, 112, 1798-1807, DOI: 10.1021/jp710104d.

(2) Curtiss, L. A.; Redfern, P. C.; Raghavachari, K., "Gaussian-4 theory," J. Chem. Phys., 2007, 126, 084108, DOI: 10.1063/1.2436888

(3) Curtiss, L. A.; Redfern, P. C.; Raghavachari, K., "Gaussian-4 theory using
reduced order perturbation theory," J. Chem. Phys., 2007, 127, 124105-8, DOI: 10.1063/1.2770701.

InChIs

Reaction 1 product: InChI=1/C2H2O3/c1-2-4-5-3-1/h1-2H

Reaction 2 product: InChI=1/C2H4O3/c1-2-4-5-3-1/h1-2H2