Archive for July, 2009

CD of high-symmetry molecules

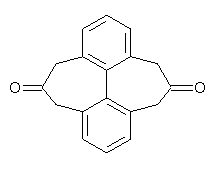
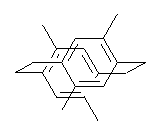
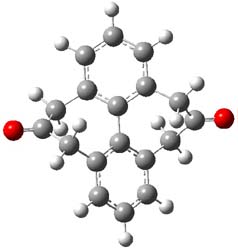
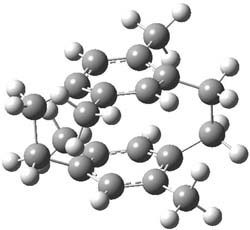
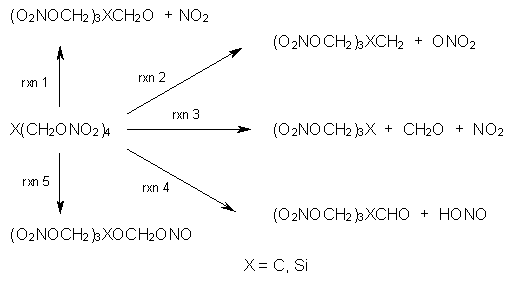
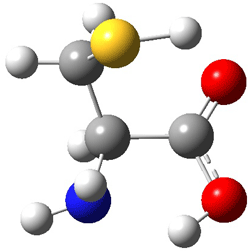
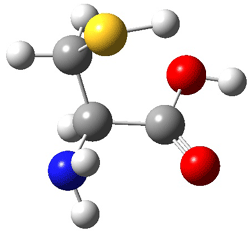
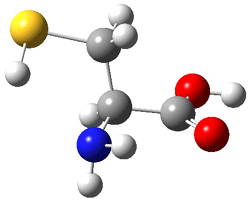
I have written a number of blog posts that deal with the computation of optical activity. Trindle and Altun have now reported TD-DFT computations of circular dichroism of high-symmetry molecules.1 The employ either B3LYP (with a variety of basis sets, the largest being 6-311++G(2d,2p)) and SOAP/ATZP. For a number of the high symmetry molecules (two examples are shown in Figure 1), the two methods differ a bit in their predictions of the first excited state, with SOAP typically predicting a red shift relative to the B3LYP. However, both methods general give the same sign of the CD signals and their line shapes are similar.


1


2

Figure 1. B3LYP/6-31G(d) optimized structures of 1 and 2 (again due to incomplete supporting materials, I reoptimized these structures)

References

(1) Trindle, C.; Altun, Z., "Circular dichroism of some high-symmetry chiral molecules: B3LYP and SAOP calculations " Theor. Chem. Acc. 2009, 122, 145-155, DOI: 10.1007/s00214-008-0494-8.

InChIs

1: InChI=1/C18H14O2/c19-15-7-11-3-1-4-12-8-16(20)10-14-6-2-5-13(9-15)18(14)17(11)12/h1-6H,7-10H2
InChIKey=DYZSIUYFWKNLHS-UHFFFAOYAB

2: InChI=1/C20H24/c1-13-9-18-7-8-20-12-15(3)19(11-16(20)4)6-5-17(13)10-14(18)2/h9-12H,5-8H2,1-4H3
InChIKey=JTMLLDPOLFRPGJ-UHFFFAOYAC

DFT &Optical Rotation Steven Bachrach 27 Jul 2009 No Comments

Si-PETN sensitivity explained

PETN C(CH2ONO2)3 is a relatively insensitive explosive. The silicon analogue Si(CH2ONO2)3 is extraordinarily sensitive, exploding at the touch of a spatula. (By the way, this makes it extremely ill-advised as an explosive – it’s way too dangerous!) Goddard employed MO6 computations to explore five different possible decomposition pathways, shown in Scheme 1.1 Reaction 1, the loss of NO2, is a standard decomposition pathway for many explosives, but the barrier for the C and Si analogues are similar and the reaction of the Si compound is not exothermic. The barrier for Reaction 2 is very large, and the barriers for the C and Si analogues for Reactions 3 and 4 are too similar to explain the differences in their sensitivities.

Scheme 1.

Reaction 5, however, does offer an explanation. The barrier for the Si analogue is 32 kcal mol-1, lower than for any other pathway, and almost 50 kcal mol-1 lower than the barrier for the rearrangement of the PETN itself. Furthermore, Reaction 5 is very exothermic for Si-PETN (-44.5 kcal mol-1), while the most favorable pathway for PETN decomposition, Reaction 1, is endothermic. Thus the small barrier and the large amount of energy released for Reaction 5 of Si-PETN suggests its extreme sensitivity.

References

(1) Liu, W.-G.; Zybin, S. V.; Dasgupta, S.; Klapötke, T. M.; Goddard III, W. A., "Explanation of the Colossal Detonation Sensitivity of Silicon Pentaerythritol Tetranitrate (Si-PETN) Explosive," J. Am. Chem. Soc. 2009, 131, 7490-7491, DOI: 10.1021/ja809725p.

InChIs

PETN: InChI=1/C5H8N4O12/c10-6(11)18-1-5(2-19-7(12)13,3-20-8(14)15)4-21-9(16)17/h1-4H2
InChIKey=TZRXHJWUDPFEEY-UHFFFAOYAE

Si-PETN: InChI=1/C4H8N4O12Si/c9-5(10)17-1-21(2-18-6(11)12,3-19-7(13)14)4-20-8(15)16/h1-4H2
InChIKey=FBKTZZKPJKPXMT-UHFFFAOYAL

DFT Steven Bachrach 20 Jul 2009 1 Comment

Cysteine conformations revisited

Schaefer, Csaszar, and Allen have applied the focal point method towards predicting the energies and structures of cysteine.1 This very high level method refines the structures that can be used to compare against those observed by Alonso2 in his laser ablation molecular beam Fourier transform microwave spectroscopy experiment (see this post). They performed a broad conformation search, initially examining some 66,664 structures. These reduced to 71 unique conformations at MP2/cc-pvTZ. The lowest 11 energy structures were further optimized at MP2(FC)/aug-cc-pV(T+d)Z. The four lowest energy conformations are shown in Figure 1 along with their relative energies.

I
(0.0)

II
(4.79)

III
(5.81)

IV
(5.95)

Figure 1. MP2(FC)/aug-cc-pV(T+d)Z optimized geometries and focal point relative energies (kJ mol-1) of the four lowest energy conformers of cysteine.1

The three lowest energy structures found here match up with the lowest two structures found by Alonso and the energy differences are also quite comparable: 4.79 kJ and 5.81 mol-1 with the focal point method 3.89 and 5.38 kJ mol-1 with MP4/6-311++G(d,p)// MP2/6-311++G(d,p). So the identification of the cysteine conformers made by Alonso remains on firm ground.

References

(1) Wilke, J. J.; Lind, M. C.; Schaefer, H. F.; Csaszar, A. G.; Allen, W. D., "Conformers of Gaseous Cysteine," J. Chem. Theory Comput. 2009, DOI: 10.1021/ct900005c.

(2) Sanz, M. E.; Blanco, S.; López, J. C.; Alonso, J. L., "Rotational Probes of Six Conformers of Neutral Cysteine," Angew. Chem. Int. Ed. 2008, 4, 6216-6220, DOI: 10.1002/anie.200801337

InChIs

Cysteine:
InChI=1/C3H7NO2S/c4-2(1-7)3(5)6/h2,7H,1,4H2,(H,5,6)/t2-/m0/s1
InChIKey: XUJNEKJLAYXESH-REOHCLBHBU

amino acids &focal point &Schaefer Steven Bachrach 13 Jul 2009 1 Comment

Hexaporphyrin that’s Möbius aromatic

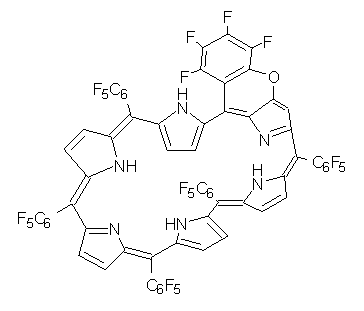
The Kim and Osuka groups have reported another Möbius aromatic porphyrin, 1, a 28 π-electron system.1 This hexaporphyrin is produced without the need for low temperature, complexation with a metal or protonation (see this post for a discussion of their earlier work). The x-ray crystal structure shows the Möbius twist, and the 1H NMR shifts of the interior protons at 2.22 and 1.03 ppm. B3LYP/6-31G** computations indicate a NICS value at the center of the molecule of -11.8 ppm. These are consistent with aromatic behavior.


1

References

(1) Tokuji, S.; Shin, J.-Y.; Kim, K. S.; Lim, J. M.; Youfu, K.; Saito, S.; Kim, D.; Osuka, A., "Facile Formation of a Benzopyrane-Fused [28]Hexaphyrin That Exhibits Distinct Möbius Aromaticity," J. Am. Chem. Soc. 2009, 131, 7240-7241, DOI: 10.1021/ja902836x.

InChIs

1: InChIKey=YGJLOPZWRVMFIJ-XFAHNSIYBC

Aromaticity Steven Bachrach 07 Jul 2009 No Comments