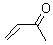
Often gem-dialkyl substitution accelerates a reaction, for example in the formation of an epoxide via reaction 1. Here the relative rates are 1:21:252 in going from 1 to 2 to 3.¹ This acceleration is the Thorpe-Ingold effect and had been suggested to arise from a steric reaction: that the methyl groups contract the angle and bring the terminal groups closer together.

1: R₁ = R₂ = H
2: R₁ = Me, R₂ = H
3: R₁ = R₂ = Me

Kostal and Jorgensen² have examined the reaction of the 2-chloroethoxides 1-3 using computations, especially to look at the effect of solvent. At MP2/6-311+G(d,p) and CBS-Q, the relative rates (based on the activation free energy ΔG^‡) are 1:2.8:17 and 1:0.7:3.7, respectively. Evidently there is no significant rate enhancement afforded by gem-substitution in the gas phase.

However, solution computations give a very different result. Using PCM along with the MP2 method, the computed relative rates are 1:5.8:1100 and with the Monte Carlo-Free Energy Perturbation method, the relative rates for aqueous solution are 1:30:773. Thus, the Thorpe-Ingold acceleration is due to solvent. Analysis of the hydrogen bonded structures and the solute-water pair distributions suggest that increasing alkyl substitution reduces the strength of solvation of the reactant, leading to the lower activation barrier.

References

(1) Jung, M. E.; Piizzi, G., "gem-Disubstituent Effect:Theoretical Basis and Synthetic Applications," Chem. Rev., 2005, 105, 1735-1766, DOI: 10.1021/cr940337h

(2) Kostal, J.; Jorgensen, W. L., "Thorpe-Ingold Acceleration of Oxirane Formation Is Mostly a Solvent Effect," J. Am. Chem. Soc., 2010, 132, 8766-8773, DOI: 10.1021/ja1023755

A real tour-de-force experimental and computational study of the ORD of 2,3-hexadiene 1 has been produced through the combined efforts of Wiberg, Jorgensen, Crawford, Cheeseman and colleagues.¹ You might not expect a simple compound like 1 to display anything particularly unusual, but you’d be wrong!

2,3-hexadiene exists as three conformations, shown in Figure 1. The cis conformers is the lowest energy form, but the other two are only 0.2 kcal mol^-1 higher in energy, meaning that all three will have significant mol fractions at 0 °C, as listed in Figure 1. The optical rotation for each conformer was determined using B3LYP/aug-cc-pVDZ and CCSD/aug-ccpVDZ. While there is some disagreement in the values determined by the two methods, what is most interesting is that large dependence of [α]_D on the conformation – see Table 1!

cis 0.0 (0.441)

gauche120 0.269 (0.280)

gauche240 0.272 (0.279)

Figure 1. CCSDT optimized geometries of 1, their relative energies (kcal mol^-1) and, in parenthesis, their mol fractions at 0 °C.¹

Table 1. Calculated [α]_D for 1.

^aUsing the aug-ccpVDZ basis set. ^aBoltzman averaged based on the populations shown in Figure 1.

The ORD spectrum of 1 was taken for neat liquid and in the gas phase. The computed and experimental optical rotations are listed in Table 2. Two interesting points can be made from this data. First, the optical activity of 1 is strongly affected by phase. Second, the computed optical rotations, especially the CCSD values, are in fairly good agreement with the gas-phase experimental values.

Table 2. Boltzmann-weighted computed and experimental optical rotations of 1.

A hypothesis to account for the large difference in the gas- and liquid-phase ORD for 1 is that the conformational distribution changes with the phase. The gas and liquid-phase ORD of 2,3-pentadiene shows the same strong phase dependence, even though this compound exists as only one conformer.

Next, a Monte Carlo simulation of gas- and liquid-phase 1 was performed to assess the conformational distributions. Though the range of dihedral angle distributions span about 60°, the population distribution is nearly identical in the two phases – there is no medium-dependence on the conformation distribution, and so this cannot explain the difference in the gas and liquid ORDs.

The authors also tested for the vibrational dependence on the optical rotation. While there is a small correction due to vibrations, it is not enough to account for the differences due to the medium. The origin of this effect remains unexplained.

References

(1) Wiberg, K. B.; Wang, Y. g.; Wilson, S. M.; Vaccaro, P. H.; Jorgensen, W. L.; Crawford, T. D.; Abrams, M. L.; Cheeseman, J. R.; Luderer, M., "Optical Rotatory Dispersion of 2,3-Hexadiene and 2,3-Pentadiene," J. Phys. Chem. A, 2008, DOI: 10.1021/jp076572o.

InChIs

1: InChI=1/C6H10/c1-3-5-6-4-2/h3,6H,4H2,1-2H3/t5-/m1/s1 InChIKey=DPUXQWOMYBMHRN-RXMQYKEDBA

Jorgensen reports an enhanced QM/MM and ab initio study of the rate enhancement of Diels-Alder reactions in various solvents.¹ This study extends earlier studies that he and others have done, many of which are discussed in Chapter 6.2 of the book. In this study, he reports QM/MM computations using the PDDG/PM3 method for the QM component, and MP2 computations incorporating CPCM to account for bulk solvent effects.

The major advance in methodology in this paper is performing a two-dimensional potential of mean force analysis where these two dimensions correspond to the forming C-C distances. In addition, computations were done for water, methanol, acetonitrile and hexane as solvents. Highlights of the results are listed in Table 1.

Table 1. Computed bond asynchronicity^a and activation energy^b (kcal/mol) for the Diels-Alder reaction with cyclopentadiene.

The semi-empirical method underestimates the asynchronicity of these gas-phase Diels-Alder TSs. However, with inclusion of the solvent, the computations do indicate a growing asynchronicity with solvent polarity, This is associated with the ability of the solvent, especially protic solvents, to preferentially hydrogen bond to the carbonyl in the TS.

In terms of energetics, in must first be pointed out that the computations dramatically overestimate the activation barriers. However, the relative trends are reproduced: the barrier increases from water to methanol to acetonitrile to hexane. Jorgensen also computed the activation barriers at MP2/6-311+G(2d,p) with CPCM using the CBS=QB3 gas phase geometries. Some of these results are listed in Table 2. The results for water are in outstanding agreement with experiment. However, the results for the other solvents are poor, underestimating the increase in barrier in moving to the more polar solvent.

Table 2. MP2/6-311+G(2d,p)/CPCM values for ΔG^‡ (kcal/mol).

Bottom line, the conclusions of this study are in agreement with the earlier studies, namely that the hydrophobic effect (better may be the enforced hydrophobic interaction) and greater hydrogen bonding in the TS (both more and stronger hydrogen bonds) account for the rate acceleration of the Diels-Alder reaction in water.

References

(1) Acevedo, O.; Jorgensen, W. L., "Understanding Rate Accelerations for Diels-Alder Reactions in Solution Using Enhanced QM/MM Methodology," J. Chem. Theory Comput. 2007, 3, 1412-1419, DOI: 10.1021/ct700078b.