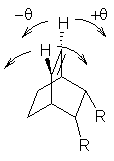
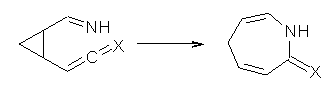
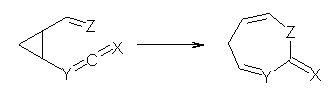
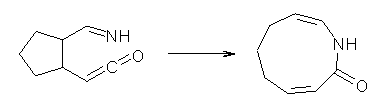
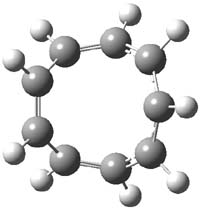
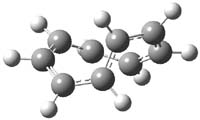
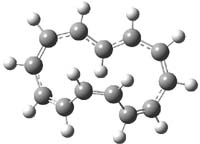
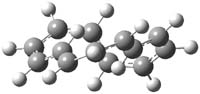
What gives rise to the face selectivity in the epoxidation of the alkene of 1 and 2? And why is the epoxidation of 3 of opposite selectivity? Williams¹ argues that the stereoinduction is due to distortional asymmetry, an argument similar to one made recently by Houk^2,3 (see this post) and others for cycloaddition reactions.

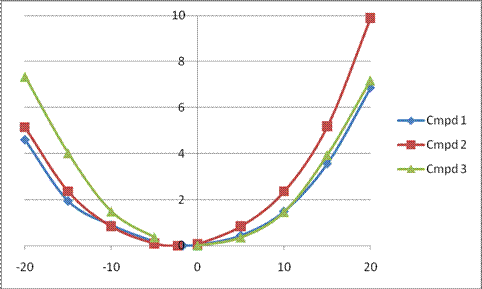
The major conclusion from this paper is drawn from the potential energy curve that results from out-of-plane bending of the alkenyl hydrogens, as in Figure 1. The bending curves (computed at B3LYP/6-31g(2d,2p)//B3LYP/6-31+G(d))) are asymmetric: bending the hydrogens away from the three-member ring requires less energy than bending them towards the cyclopropyl ring. However, for 3, bending in the two directions is pretty similar, with a slight preference for bending towards the four-member ring.

Fig. 1 Energy (kcal mol^-1) vs distortion angle of alkenyl hydrogens

This type of bending is part of the distortions that have to occur to reach the transition state, and so Williams argues that the attack from the cyclopropyl face by the oxidant is preferred because of the easier geometric distortion of moving the hydrogen away. Williams makes standard orbital interaction arguments to rationalize the distortion preference.

References

(1) Kolakowski, R. V.; Williams, L. J., "Stereoinduction by distortional asymmetry," Nat. Chem. 2010, 2, 303-307, DOI: 10.1038/nchem.577.

(2)
Xu, L.; Doubleday, C. E.; Houk, K. N., "Dynamics of 1,3-Dipolar Cycloaddition Reactions of Diazonium Betaines to Acetylene and Ethylene: Bending Vibrations Facilitate Reaction," Angew. Chem. Int. Ed. 2009, 48, 2746-2748, DOI: 10.1002/anie.200805906

(3) Xu, L.; Doubleday, C. E.; Houk, K. N., "Dynamics of 1,3-Dipolar Cycloadditions: Energy Partitioning of Reactants and Quantitation of Synchronicity," J. Am. Chem. Soc., 2010, 132, 3029–3037, DOI: http://dx.doi.org/10.1021/ja909372f

InChIs

1: InChI=1/C9H12/c1-2-7-4-3-6(1)8-5-9(7)8/h1-2,6-9H,3-5H2
InChIKey=YNSKHNKUOPTLCL-UHFFFAOYAA

2: InChI=1/C10H11N/c11-5-8-9-6-1-2-7(4-3-6)10(8)9/h1-2,6-10H,3-4H2
InChIKey=XHTNELKCCFLXEU-UHFFFAOYAJ

3: InChI=1/C10H14/c1-2-8-4-3-7(1)9-5-6-10(8)9/h1-2,7-10H,3-6H2
InChIKey=OYPVZSANECKQOK-UHFFFAOYAR

Rzepa has published a theoretical study of potential stable molecules containing a bond to helium.¹ The work was inspired by the post on this blog pertaining to potential hypervalent carbon species that mimic the S_N2 transition state. Rzepa first reported some of his results on his own blog (see this post and previous ones). The upshot is that structures like 1 appear to possess real bonds to helium!

1

As always, Henry has deposited his structures (see here) and so I have not reproduced any structures.

As an aside I am greatly inspired by this paper as offering an example of how non-traditional media – our two blogs – led to new science, and one that was published by a very forward-thinking publisher (Nature), who recognizes the value of new technologies that facilitate (and not degrade nor supplant) the traditional scientific communication media.

References

1) Rzepa, H. S., “The rational design of helium bonds,” Nature Chem., 2010, 2, 390-393, DOI:10.1038/nchem.596.

Kemnitz and co-workers have added to the protobranching debate (see these earlier posts i, ii, iii) with a proposal for how branching can be stabilizing.¹ A normal chemical bond can be described within the valence bond prescription as an interplay of three different contributors: a covalent term (a) and two ionic terms (b and c). For a typical covalent bond, term a dominates, and for the recently proposed “charge-shift” bond (see this post), the ionic VB terms dominate.

Kemnitz now examines propane using a valence bond method and finds the following. The dominant VB term is the standard, two-covalent bond structure I. Next in importance are the single bond ionic VB structures II. Lastly, the 1,3-ionic structures III contribute about 9% to the total VB wavefunction. These contributions are only possible with branching and provide a net stabilization of about 1.6 kcal mol^-1. This energy is nearly identical to the stabilization energy associated with the protobranching concept proposed by Schleyer, Houk and Mo. This type of ionic structure just might be the mechanism for protobranching stabilization.

References

(1) Kemnitz, C. R.; Mackey, J. L.; Loewen, M. J.; Hargrove, J. L.; Lewis, J. L.; Hawkins, W.
E.; Nielsen, A. F., "Origin of Stability in Branched Alkanes," Chem. Eur. J. 2010, 16,6942-6949, DOI: 10.1002/chem.200902550

Duncan has discovered a pseudopericyclic [3,3]-sigmatropic rearrangement, ¹ and what is particularly interesting is how rare this seems to be! (See this post for an earlier related study.) Using CASSCF/6-31G* computations of Reactions 1-9, only Reaction 1 is found to be pseudopericyclic. (The transition state for this reaction is shown in Figure 1). This characterization is based largely on the shapes of the active MOs, one of which displays two orbital disconnections. In addition, this transition state is much more planar than is typical for a [3,3]-rearrangement. Dihedral angles are about 20 ° in the TS for reaction 1, while in the other reaction TSs, their dihedral angless are about 50 ° or even larger. This is consistent with Birney’s contention that pseudopericyclic reactions have nearly planar TSs. The activation barrier for Reaction 1 is also quite small, 19.4 kcal mol^-1, much lower than for Reactions 2 (26.2 kcal mol^-1) and 3 (33.1 kcal mol^-1).

Figure 1. CASSCF/6-31G* optimized TS for Reaction 1.

References

(1) Forte, L.; Lafortune, M. C.; Bierzynski, I. R.; Duncan, J. A., "CASSCF Molecular Orbital Calculations Reveal a Purely Pseudopericyclic Mechanism for a [3,3] Sigmatropic Rearrangement," J. Am. Chem. Soc., 2010, 132, 2196-2201, DOI: 10.1021/ja906679g

InChIs

Reaction 1:
Reactant (2-(2-methanimidoylcyclopropyl)ethenone):
InChI=1/C6H7NO/c7-4-6-3-5(6)1-2-8/h1,4-7H,3H2
InChIKey=FMPHPBIFFKHFNF-UHFFFAOYAG
Product (1,4-dihydroazepin-7-one):
InChI=1/C6H7NO/c8-6-4-2-1-3-5-7-6/h2-5H,1H2,(H,7,8)/f/h7H
InChIKey=BEYCJMUGQZWVBC-QDQILVOLCK

Since Heilbronner¹ proposed the Möbius annulene in 1964, organic chemists have been fascinated with this structure and many have tried to synthesize an example. I have written many blog posts (1, 2, 3, 4, 5) related to computed Möbius compounds. Now, Herges and Grimme and co-workers have looked at cationic Möbius annulenes.

For the [9]annulene cation,² a variety of DFT methods, along with SCS-MP2 and CCSSD(T) computations suggest that the lowest energy Hückel (1h) and Möbius (1m) structures, shown in Figure 1, are very close in energy. In fact, the best estimate (CCSD(T)/CBS) is that they differ by only 0.04 kcal mol^-1. Laser flash photolysis of 9-chlorobicyclo[6.1.0]nona-2,4,6-triene suggest however that only the Hückel structure is formed, and that its short lifetime is due to rapid electrocyclic ring closure.

In a follow-up study, Herges has examined the larger annulene cations, specifically [13]-, [17]- and [21]-annulenes. ³ The Möbius form of [13]-annulene cation (2m) is predicted to be 11.0 kcal mol^-1 lower in energy that the Hückel (2h) form at B3LYP/6-311+G**. The structures of these two cations are shown in Figure 1. The Möbius cation 2m is likely aromatic, having NICS(0)= -8.95. Electrocyclic ring closure of 2m requires passing through a barrier of at least 20 kcal mol^-1, suggesting that 2m is a realistic target for preparation and characterization.

1h	1m
2h	2m

Figure 1. Optimized structures of 1 (CCSD(T)/cc-pVTZ)² and 2 (B3LYP/6-311+G**)³.

The energy difference between the Möbius and Hückel structures of the larger annulenes is very dependent on computational method, but in all cases the difference is small. Thus, Herges concludes that [13]-annulene cation should be the sole target of synthetic effort toward identification of a Möbius annulene. Experimental studies are eagerly awaited!

References

(1) Heilbronner, E., “Huckel molecular orbitals of Mobius-type conformations of annulenes,” Tetrahedron Lett., 1964, 5, 1923-1928, DOI: 10.1016/S0040-4039(01)89474-0.

2) Bucher, G.; Grimme, S.; Huenerbein, R.; Auer, A. A.; Mucke, E.; Köhler, F.; Siegwarth, J.; Herges, R., "Is the [9]Annulene Cation a Möbius Annulene?," Angew. Chem. Int. Ed., 2009, 48, 9971-9974, DOI: http://dx.doi.org/10.1002/anie.200900886

(3) Mucke, E.-K.; Kohler, F.; Herges, R., "The [13]Annulene Cation Is a Stable Mobius Annulene Cation," Org. Lett., 2010, 12, 1708–1711, DOI: 10.1021/ol1002384

InChIs

1: InChI=1/C9H9/c1-2-4-6-8-9-7-5-3-1/h1-9H/q+1/b2-1-,5-3-,6-4-,9-7-
InChIKey=LIUDWUIEJKKGNI-BWYSQNKRBF

2: InChI=1/C13H13/c1-2-4-6-8-10-12-13-11-9-7-5-3-1/h1-13H/q+1/b2-1-,5-3-,6-4-,9-7-,10-8-,13-11-
InChIKey=FUBPZYTZTJGXKZ-OGBOFXOGBR