Dynamic effects rear up yet again in a seemingly simple reaction. Singleton has examined the Diels-Alder cycloaddition of acrolein with methyl vinyl ketone to give two cross products 1 and 2.¹ Upon heating the product mixture, 1 is essentially the only observed species. The retro-Diels-Alder is much slower than the conversion of 2 into 1. Using a variety of rate data, the best estimate for the relative formation of 1:2 is 2.5.

The eight possible transition states for this reaction were computed with a variety of methodologies, all providing very similar results. The lowest energy TS is TS3. A TS of type TS4 could not be found; all attempts to optimize it collapsed to TS3.

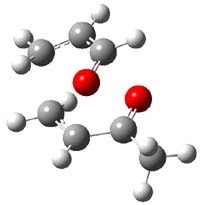
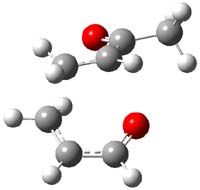
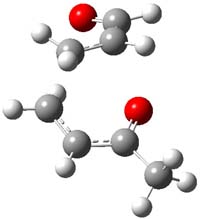
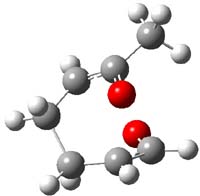
IRC computations indicate the TS3 leads to 1. The lowest energy TS that leads to 2 is TS6, but a second TS (TS5) lower in energy than TS6 also leads to 1. The other TS are still higher in energy. A Cope-type TS that interconverts 1 and 2 (TS7) was also located. The geometries of these TSs are shown in Figure 1.

TS3 (0.0)	TS5 (4.2)
TS6 (5.2)	TS7 (-0.4)

Figure 1. MP2/6-311+G** optimized geometries and relative energies (kcal mol^-1) of TS3-TS7.¹

Ordinary transition state theory cannot explain the experimental results – the energy difference between the lowest barrier to 1 (TS3) and to 2 (TS6) suggests a rate preference of over 700:1 for 1:2. But the shape of the potential energy surface is reminiscent of others that have been discussed in both my book (Chapter 7) and this blog (see my posts on dynamics) – a surface where trajectories cross a single TS but then bifurcate into two product wells.

To address the chemical selectivity on a surface like this, one must resort to molecular dynamics and examine trajectories. In their MD study of the 296 trajectories that begin at TS3 with motion towards product, 89 end at 1 and 33 end at 2, an amazingly good reproduction of experimental results! Interestingly, 174 trajectories recross the transition state and head back towards reactants. These recrossing trajectories result from “bouncing off” the potential energy wall of the forming C₄-C₅ bond.

In previous work, selectivity in on these types of surfaces was argued in terms of which well the TS was closer to. But analysis of the trajectories in this case revealed that a strong correlation exists between the initial direction and velocity in the 98 cm^-1 vibration – the vibration that corresponds to the closing of the second σ bond, the one between C₆-O₁ (forming 1), in the negative direction, and closing the C­₃-O₈ bond (forming 2) in the positive direction. Singleton argues that this is a type of dynamic matching, and it might be more prevalent that previously recognized.

References

(1) Wang, Z.; Hirschi, J. S.; Singleton, D. A., "Recrossing and Dynamic Matching Effects on Selectivity in a Diels-Alder Reaction," Angew. Chem. Int. Ed., 2009, 48, 9156-9159, DOI: 10.1002/anie.200903293

InChIs

1: InChI=1/C7H10O2/c1-6(8)7-4-2-3-5-9-7/h3,5,7H,2,4H2,1H3
InChIKey=AOFHZPHBPUYLAG-UHFFFAOYAJ

2: InChI=1/C7H10O2/c1-6-3-2-4-7(5-8)9-6/h3,5,7H,2,4H2,1H3
InChIKey=PLZQHPPETMMEED-UHFFFAOYAD

Houk and Doubleday have a nice follow-up study¹ to their previous MD study² of 1,3-dipolar cycloadditions, which I posted on here. They report on the cycloaddition of either acetylene or ethylene to 9 different 1,3-dipoles. Continuing on Houk’s recent thread of looking at distortion energies to attain the TS, they note that a sizable fraction (often over 50%) of the distortion energy is associated with bending the X-Y-Z bond of the dipole, consistent with their earlier work suggesting the importance of this vibration in attaining and crossing the TS. What’s new in this paper is the extensive MD studies, with trajectory studies of all 18 reactions. These revealed again the importance of vibrational energy in this X-Y-Z bending mode in crossing the TS. They also noted the role of translational energy, and the relationship between translational vs. vibrational energy depending on the early/late nature of the TS. Their final point was that the lifetime of any diradical or diradical-like intermediate is so short, less than the time of a bond vibration, so that one can discount any diradical participation. The reaction is concerted.

References

(1) Xu, L.; Doubleday, C. E.; Houk, K. N., "Dynamics of 1,3-Dipolar Cycloadditions: Energy Partitioning of Reactants and Quantitation of Synchronicity," J. Am. Chem. Soc., 2010, ASAP, DOI: /10.1021/ja909372f

(2) Xu, L.; Doubleday, C. E.; Houk, K. N., "Dynamics of 1,3-Dipolar Cycloaddition Reactions of Diazonium Betaines to Acetylene and Ethylene: Bending Vibrations Facilitate Reaction," Angew. Chem. Int. Ed., 2009, 48, 2746-2748, DOI: 10.1002/anie.200805906

An interesting little discussion on the meaning of “protobranching” appears in a comment¹ and reply² in J. Phys. Chem. A. Fishtik¹ calls out the concept of protobranching on three counts:

1. It is inconsistent to count a single protobranch for propane, but then not have three protobranches in cyclopropane
2. It is inappropriate to utilize methane as a reference species.
3. Group additivities work well.

I tend to side more with Schleyer² in his rebuttal of these charges, and so will present from this perspective. First off, Schleyer argues that he can define protobranch anyway he wants! (He in fact cites a quote of Humpty Dumpty from Lewis Carroll to support this stance!) Schleyer is of course correct. Fishtik should really have argued “Does Schleyer’s definition of protobranch add to our understanding of strain?” So Fishtik claims that there is an internal inconsistency in Schleyer’s definition – taking the view point that the C-(C)₂(H)₂ group is identical to the protobranch. Schleyer counters that no, the protobranch is this group along with the caveat that the two terminal carbons are not connected, like they are in cyclopropane. I really prefer Gronert’s approach here – where he argues for just what are the implications of Schleyer’s definition (see this post).

Fishtik refuses to use methane as a reference since it is a unique molecule. Again, if one takes the group-centric view, then methane possesses a group that no other compound has. But Schleyer counters that one is free to choose whatever reference one thinks is appropriate, just be sure to understand what properties are conserved or not conserved when using that reference selection. To me, this is really the key for the entire discussion: choose one’s references in such a way as to minimize differences between your reference compound(s) and the molecule(s) you are trying to explore to just the property of interest. So, if one is interested in quantifying ring strain, the reference compounds should be not only be strain-free but they should differ in no other way from the cyclic molecule other than the presence of the ring! Unfortunately, there is no unique or non-arbitrary way to do this! Schleyer’s approach and Fishtik’s approach differ in just what properties they believe are important to conserve and which properties they are going to lump into the concept “ring strain”.

Fishtik shows a whole slew of reactions that demonstrate the consistency of group additivity methods. Schleyer correctly points out that these examples are really intimately related and represent only one type of definition. Again, there is really no unique set of references, and many, many different models have been developed, all of which can match experimental data quite well – like for example heats of formation. The key is what these models say in terms of interpreting, say, these heats of formation. Can one rationalize trends and make predictions with the model? If so, then it has utility. If not, then the model should be discarded. Ultimately, Fishtik’s argument is that the protobranching model does not assist us in understanding strain – Schleyer would obviously beg to differ!

References

(1) Fishtik, I., "Comment on "The Concept of Protobranching and Its Many Paradigm Shifting Implications for Energy Evaluations"," J. Phys. Chem. A, 2010, ASAP, DOI: 10.1021/jp908894q

(2) Schleyer, P. v. R.; McKee, W. C., "Reply to the "Comment on ‘The Concept of Protobranching and Its Many Paradigm Shifting Implications for Energy Evaluations’"," J. Phys. Chem. A, 2010, ASAP, DOI: 10.1021/jp909910f

One more study of cyclodiene reactions with ketenes that suggest the occurrence of dynamic effects.¹ The reaction of cyclopentadiene with t-butylcyanoketene 1 gives cyclobutanone 2 solely. In contrast, the reaction of 1,3-cyclophexadiene with 1 gives the cyclobutanone 3 and a small amount (less than 25%) of the ether 4. Warming the reaction from -20 °C to 20 °C leads to loss of 3 and an increase in 4. This is in distinct contrast with the reaction of cyclopentadiene with diphenylketene,² where the ether product is the major product and the cyclobutenone is the minor product (see Chapter 7.3.5.2 in my book).

To help understand this situation, the authors optimized the structures of the critical points on the surface of the cyclohexadiene reaction at MPWB1K/6-31+G(d,p) – though once again, there are no supporting materials so I cannot supply the 3-D structures in the blog! 4 is predicted to be 3.4 kcal mol^-1 more stable than 3, which accounts for it being the thermodynamic product, consistent with experiment. Only two transition states are found. The first TS, with a barrier of 23.2 kcal mol^-1, connects reactants with 3. The second transition state corresponds to the oxy-Cope rearrangement that takes 3 into 4. This surface is reminiscent of many others that display dynamic effects (again see my book and also these posts). Unfortunately, the authors have not performed any trajectory calculation. But one might expect that most trajectories cross the first transition state and fall into the well associated with 3. Some of these molecules then go on to cross the second barrier to form 4. But some trajectories cross the first TS and then veer off into the slightly lower well associated with 4, being directly formed from reactant. This would be a manifestation of dynamic effects, and is worth further study.

References

(1) Marton, A.; Pârvulescu, L.; Draghici, C.; Varga, R. A.; Gheorghiu, M. D., "Reaction of Moore’s ketene (tert-butylcyanoketene) with 1,3-cyclopentadiene and 1,3-cyclohexadiene. Is periselectivity controlled by the dynamic of trajectories at the bifurcation point?," Tetrahedron, 2009, 65, 7504-7509, DOI: 10.1016/j.tet.2009.07.020.

(2) Ussing, B. R.; Hang, C.; Singleton, D. A., "Dynamic Effects on the Periselectivity, Rate, Isotope Effects, and Mechanism of Cycloadditions of Ketenes with Cyclopentadiene," J. Am. Chem. Soc., 2006, 128, 7594-7607, DOI: 10.1021/ja0606024.