Here’s a real tour de force study combining exciting experiments with detailed computations. It’s a look at the radical cation of propellane performed by Bally and Williams.¹ This paper has been nicely reviewed by Hiberty.²

Propellane 1, whose bridgehead-bridgehead bond has been a topic of an earlier post, has a HOMO that is largely outside of the bridgehead-bridgehead region. Thus, loss of an electron to form the radical cation 1^.+ seems unlikely to lead to any significant geometrical change. However, the ESR of the radical cation of propellane shows two types of hydrogens, one type of four hydrogens and a second type of two hydrogens. This is incompatible with a D_3h structure similar to that of 1. Furthermore, loss of an electron from dimethylenecyclopropane 2 leads to a species whose ESR is nearly identical to that of the radical cation of propellane. Analysis of the ESR suggests that the radical actually produced is 3^.+.

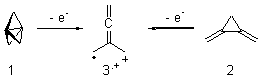
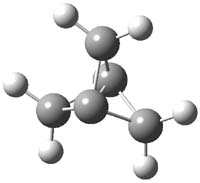
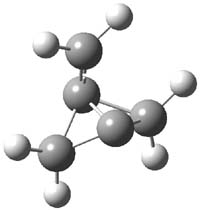
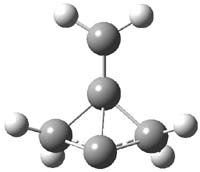
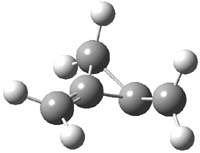
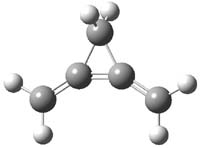
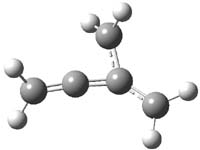
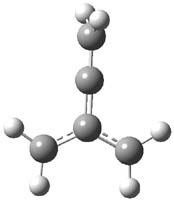
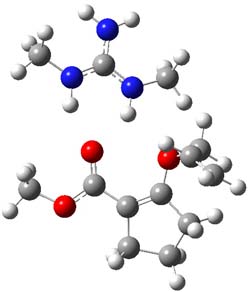
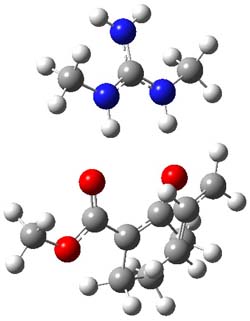
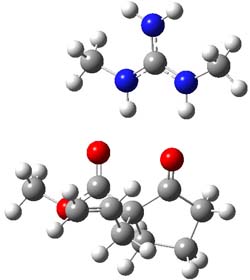
CCSD(T)/cc-pVTZ//B3LYP/6-31G* computations were performed to try to discern a mechanism for this rearrangement. The D_3h structure of 1^.+ is a local energy minimum with most computational methods, though not with B3LYP, where it is a TS connecting mirror image C₂ structures. Breaking symmetry to C₂ leads to a TS (TS1) for cleaving one of the C-C_bridgehead bonds. This TS is only 1.15 kcal mol^-1 above 1^.+, and leads to 4^.+, 7.38 kcal mol^-1 below 1^.+. Cleavage of a second C-C_bridgehead bond passes through TS2, with a barrier from 4^.+ of only 2.89 kcal mol^-1. This leads to 2^.+. Lastly, cleavage of a third C-C_bridgehead bond through TS3, with a barrier of only 2.09 kcal mol^-1 above 2^.+, leads to 3^.+, overall 30.4 kcal mol^-1 exothermic from 1^.+. The structures of these critical points are shown in Figure 1. Quite a neat little pathway – three sequential bond ruptures without ever cleaving what was the weakest bond in the original compound (the bridgehead-bridgehead bond)!

1.+ 0.0	TS1 +1.15
4.+ -7.38	TS2 -4.49
2.+ -24.54	TS3 -22.45
3.+ -30.41

Table 1. B3LYP/6-31G* optimized critical points on the pathway of 1^.+ to 3^.+.
Relative energies in kcal mol^-1

The cool part of this is why the barrier is so small leading out of 1^.+ – vibronic coupling via C_s distortion of 1^.+ with its first excited state leads to an energy lowering of this pathway. This sort of vibronic coupling had in fact been implicated by Heilbronner and Wiberg³ in arguing the photoelectron spectrum of 1.

References

(1) Müller, B.; Bally, T.; Pappas, R.; Williams, F., "Spectroscopic and Computational Studies on the Rearrangement of Ionized [1.1.1]Propellane and Some of its Valence Isomers: The Key Role of Vibronic Coupling," J. Am. Chem. Soc. 2010, 132, 14649-14660, DOI: 10.1021/ja106024y

(2) Hiberty, P. C., "Vibronic coupling: Cage-breaking cascade," Nat. Chem. 2011, 3, 96-97, DOI: 10.1038/nchem.971

(3) Honegger, E.; Huber, H.; Heilbronner, E.; Dailey, W. P.; Wiberg, K. B., "The PE spectrum of [1.1.1]propellane: evidence for a non-bonding MO?," J. Am. Chem. Soc., 1985, 107, 7172-7174, DOI: 10.1021/ja00310a068

InChI

1: InChI=1/C5H6/c1-4-2-5(1,4)3-4/h1-3H2
InChIKey=ZTXSPLGEGCABFL-UHFFFAOYAJ

2: InChI=1/C5H6/c1-4-3-5(4)2/h1-3H2
InChIKey=ZNKWTJLYBOAVHI-UHFFFAOYAT

3^.+: InChI=1/C5H6/c1-4-5(2)3/h1-3H2/q+1
InChIKey=BVWPXIKADZQKEJ-UHFFFAOYAU

Once again, into the breach…

Ess, Liu, and De Proft offer another analysis of the protobranching effect.¹ As a reminder, Schleyer, Mo and Houk and coworkers argue that the reason why branched alkanes are more stable than linear ones is a stabilizing 1,3-interaction that they call protobranching.² This proposal has been met with both supporters and vigorous attacks – see these posts.

What is new here is a partitioning of the total DFT energy into three terms. The critical term is one based on the Weizäcker kinetic energy, which is defined as the integral of the gradient of the density squared divided by the density. They call this a “steric energy term”. The second term is the standard electrostatic term, and the last term, which really just picks up the slack, is a “fermionic quantum term”.

Using this partition, they examine a series of bond separation reactions involving alkanes with differing degrees of “protobranches”. The upshot is that the steric energy, which is destabilizing, is less in branched alkanes that linear ones. However, the fermionic quantum term essentially cancels this out, as branched alkanes, being more compact, are more destabilized by this fermionic effect than are linear alkanes. So, the only remaining term, electrostatics is responsible for the branched alkanes being more stable than linear alkanes.

This does not ultimately resolve the issue of whether the protobranching effect, as defined by Schleyer, Mo and Houk, is real, but these authors purposely chose to avoid that question.

References

(1) Ess, D. H.; Liu, S.; De Proft, F., "Density Functional Steric Analysis of Linear and Branched Alkanes," J. Phys. Chem. A, 2010, ASAP, DOI: 10.1021/jp108577g

(2) Wodrich, M. D.; Wannere, C. S.; Mo, Y.; Jarowski, P. D.; Houk, K. N.; Schleyer, P. v. R., "The Concept of Protobranching and Its Many Paradigm Shifting Implications for Energy Evaluations," Chem. Eur. J. 2007, 13, 7731-7744, DOI: 10.1002/chem.200700602

Jacobsen reports another interesting example of organocatalysis, here using a chiral guanadinium salt to catalyze the enantioselective Claisen rearrangement.¹ As an example, Reaction 1 proceeds in 6 days at 30 °C to give 81% yield with an ee of 84%. The system is also diastereoselective, so that Reaction 2, run for 6 days at 40 °C, gives an 82% yield with a diastereomeric ratio of 16:1 and an ee of 81%.

B3LYP/6-31G(d,p) computations provide some insight. The uncatalyzed reaction of 1 to give 2 is predicted to be exothermic by 16.1 kcal mol^-1, with an activation energy of 25.9 kcal mol^-1. Using N,N’-dimethylguanidnium as a model for the catalyst (and with no counter anion and no treatment of solvent – hexanes in this case), they find a complexation energy of almost 27 kcal mol^-1 for forming 3. 3 exhibits (See Figure 1) three hydrogen bond-like interactions – one N-H bifurcates to interact with the carbonyl oxygen and (a very long interaction) to the other oxygen. The product complex 4 also shows three hydrogen bond-like interactions, with an overall exothermicity of -14.7 kcal mol^-1. The complexed transition state 5 has two normal length hydrogen bonds, with an activation energy above 3 of 20.6 kcal mol^-1. Thus the complex lowers the barrier by about 5 kcal mol^-1, indicating the catalytic effect. They have not however addressed the enantioselectivity.

3	5
4

Figure 1. B3LYP/6-31G(d,p) optimized geometries of 3-5.

References

(1) Uyeda, C.; Rötheli, A. R.; Jacobsen, E. N., "Catalytic Enantioselective Claisen Rearrangements of O-Allyl β-Ketoesters," Angew. Chem. Int. Ed., 2010, 49, 9753–9756, DOI: 10.1002/anie.201005183

InChIs

1: InChI=1/C10H14O3/c1-3-7-13-9-6-4-5-8(9)10(11)12-2/h3H,1,4-7H2,2H3
InChIKey=NASFSRKGDOBHIX-UHFFFAOYAC

2: InChI=1/C10H14O3/c1-3-6-10(9(12)13-2)7-4-5-8(10)11/h3H,1,4-7H2,2H3/t10-/m0/s1
InChIKey=QXKXLNGEBVMWLH-JTQLQIEIBT

The most favorable conformation of a carboxylic acid is the Z form. In fact, the E form is rarely found. Schreiner now offers an explanation for why this is so.¹

Photolysis of matrix-deposited benzoic acid revealed only the Z form (1Z). However, photolysis of deuterated benzoic acid did reveal the E form 1E, however it disappeared with a half-life of 12 minutes on argon at 11 K and 20 K. The lack of temperature dependence, and the huge isotope effect suggested that the isomerization proceeds via tunneling.

The tunneling rate was computed by generating the reaction path at CCSD(T)/cc-pVTZ with
MP2/cc-pVDZ zero point energy. This gave a half-life of 2.8 h for the deuterium species and 10^-5 min for the proton species. A Hammet-like relationship could be produced for the half-lives of para-substituted benzoic acids. Interestingly, a nice correlation is found between the computed width of the tunneling barrier and the half life with σ-donating ability.

References

(1) Amiri, S.; Reisenauer, H. P.; Schreiner, P. R., "Electronic Effects on Atom Tunneling: Conformational Isomerization of Monomeric Para-Substituted Benzoic Acid Derivatives," J. Am. Chem. Soc., 2010, 132 , 15902–15904, DOI: 10.1021/ja107531y

InChIs

Benzoic acid: InChI=1/C7H6O2/c8-7(9)6-4-2-1-3-5-6/h1-5H,(H,8,9)/f/h8H
InChIKey=WPYMKLBDIGXBTP-FZOZFQFYCI