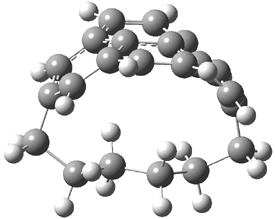
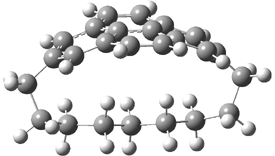
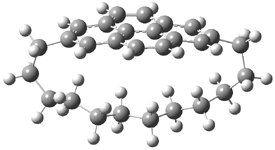
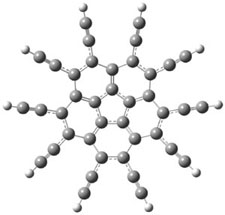
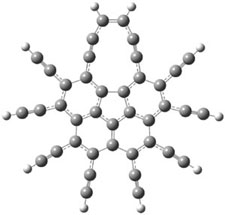
Here’s another attempt (almost successful!) in creating a planar cyclooctatetraene. Nishininaga and Iyoda have fused silicon and sulfur bridges to the COT framework, hoping to force the 8-member ring out of its preferred tub-shape into a planar structure.1 They report the synthesis of 1, 2, and 3b along with their x-ray structures. They also calculated the structures at B3LYP/6-31G(d,p) for 1-4 , and these optimized structures are shown in Figure 1.

|
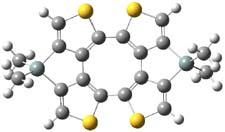
1 |
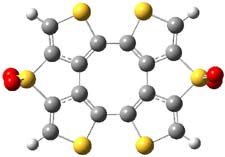
2 |
|
3a |
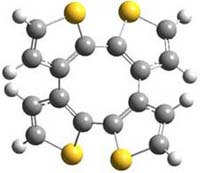
4 |
Figure 1. B3LYP/6-31G(d,p) optimized geometries of 1-4. The experimental (top) and computed (Bottom in italics) value of α are listed for each compound.1
The bent angle α is defined at the angle between the two planes that define the bottom of the tub and one of the sides. For COT itself, this angle is 40°, decidedly non-planar – as expected for a molecule avoiding the antiaromatic character it would have in its planar conformation. The computed and experimental values of α are shown in Figure 1. 4 is tub shaped. The value of α for 1 is about 18° – still tub shaped but flattened. But 2 and 3 are nearly planar, with experimental values of α about 3° and the computed values are similar.
So what is the character of the 8-member ring in these compounds. The computed NICS(0) values are 3.8 ppm for 4, the expected small value for a non-aromatic compound. (Note that the NICS value for COT is 2.9 ppm.) The values are much more positive for the other compounds: 12.7 ppm for 1, 17.4 ppm for 2, and 15.4 ppm for 3a. These compounds therefore display antiaromatic character yet they are isolable compounds!
References
(1) Ohmae, T.; Nishinaga, T.; Wu, M.; Iyoda, M., "Cyclic Tetrathiophenes Planarized by Silicon and Sulfur Bridges Bearing Antiaromatic Cyclooctatetraene Core: Syntheses, Structures, and Properties," J. Am. Chem. Soc., 2009, 132, 1066-1074, DOI: 10.1021/ja908161r
InChIs
1: InChI=1/C20H16S4Si2/c1-25(2)9-5-21-17-13(9)14-10(25)6-22-18(14)20-16-12(8-24-20)26(3,4)11-7-23-19(17)15(11)16/h5-8H,1-4H3/b19-17-,20-18-
InChIKey=DAVVQYAXJVCICC-CLFAGFIQBV
2:
3a: InChI=1/C16H4O4S6/c17-25(18)5-1-21-13-9(5)10-6(25)2-23-15(10)16-12-8(4-24-16)26(19,20)7-3-22-14(13)11(7)12/h1-4H/b14-13-,16-15-
InChIKey=VIDZCGPUBZEACC-RFIZXXDFBR
3b: InChI=1/C28H36O4S6Si4/c1-39(2,3)25-21-13-14-19(35-26(40(4,5)6)22(14)37(21,29)30)20-16-15-18(17(13)33-25)34-27(41(7,8)9)23(15)38(31,32)24(16)28(36-20)42(10,11)12/h1-12H3/b18-17-,20-19-
InChIKey=XXCFCYWSFICMIO-RXGVRZIVBS
4: InChI=1/C16H8S4/c1-5-17-13-9(1)10-2-6-18-14(10)16-12(4-8-20-16)11-3-7-19-15(11)13/h1-8H/b10-9-,12-11-,15-13-,16-14-
InChIKey=RSNUTSCZGMAXQJ-FNJUYVFOBD