A couple of years ago Ess and Houk described computations on the cycloaddition reactions of ethene and ethyne with 9 different 1,3-dipoles 1-9.1,2 Two interesting results were noted: (a) though barrier heights systematically decreased with the decreasing HOMO-LUMO gap of the 1,3-dipole, the reaction barriers are the same for a given dipole with either ethane or ethyne; (b) The TS geometries about the ethane and ethyne fragments are similar, even though the reactions are quite different in overall reaction energies. This implies a violation of the Hammond Postulate.
|
Diazonium betaines
|

|
|
Nitrilium betaines
|
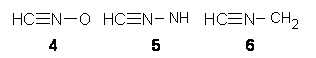
|
|
Azomethine betaines
|

|
Ess and Houk suggested that what dictated these reactions were the energies of distortion of the 1,3-dipole. This is the energy needed to distort the 1,3-dipole into its geometry in the TS. This is typically associated with the bending about the central atom, but rehybridization at the
terminal positions is also needed in many cases. A plot of the distortion energy against the activation barrier gives a line with an R2 value of 0.97.
Now Braida, Hiberty and coworkers have employed valence bond computations to interpret these findings.3 The 1,3-dipoles are composed of three valence bond structures a, b and c (shown for 1 below). The last structure (c) is the one associated with the cycloaddition reaction, as it is set up for making the two new bonds at the terminal positions.

The coefficients associated with these VB structures are given in Table 1. It is readily apparent that the degree of diradical character varies considerably among these compounds. Furthermore, for each set of 1,3-dipoles, increasing diradical content correlates with a decreased activation barrier. They also note a strong correlation of decreasing energy needed to excite the ground state 1,3-dipole to the diradical structure (of either the ground state geometry or in the TS geometry) with decreasing activation barrier. Thus, they conclude that it is the diradical character of the 1,3-dipole that controls the reaction – greater diradical character translates into a lower barrier. They argues that the concerted reaction proceeds in two phases, the first phase is distortion of the 1,3-dipole to create sufficient diradical character, and a second phase where the new bonds are made to the dipolarophile, independent of just what that dipolarophile happens to be.
Table 1. Coefficients of the 3 valence bond structures a-c for the ground state 1,3-dipoles 1-9.
|
1,3-dipole
|
a
|
b
|
c
|
|
|
1
|
0.55
|
0.24
|
0.22
|
|
2
|
0.43
|
0.32
|
0.25
|
|
3
|
0.32
|
0.41
|
0.28
|
|
4
|
0.58
|
0.21
|
0.21
|
|
5
|
0.38
|
0.36
|
0.26
|
|
6
|
0.26
|
0.48
|
0.26
|
|
7
|
0.48
|
0.18
|
0.34
|
|
8
|
0.38
|
0.24
|
0.38
|
|
9
|
0.29
|
0.29
|
0.41
|
|
References
(1) Ess, D. H.; Houk, K. N., "Distortion/Interaction Energy Control of 1,3-Dipolar
Cycloaddition Reactivity," J. Am. Chem. Soc., 2007, 129, 10646-10647, DOI: 10.1021/ja0734086
(2) Ess, D. H.; Houk, K. N., "Theory of 1,3-Dipolar Cycloadditions: Distortion/Interaction and Frontier Molecular Orbital Models," J. Am. Chem. Soc., 2008, 130, 10187-10198, DOI: 10.1021/ja800009z
(3) Braida, B.; Walter, C.; Engels, B.; Hiberty, P. C., "A Clear Correlation between the Diradical Character of 1,3-Dipoles and Their Reactivity toward Ethylene or Acetylene," J. Am. Chem. Soc., 2010, 132, 7631-7637, DOI: 10.1021/ja100512d
InChIs
1: InChI=1/N2O/c1-2-3
InChIKey=GQPLMRYTRLFLPF-UHFFFAOYAP
2: InChI=1/HN3/c1-3-2/h1H
InChIKey=JUINSXZKUKVTMD-UHFFFAOYAO
3: InChI=1/CH2N2/c1-3-2/h1H2
InChIKey=YXHKONLOYHBTNS-UHFFFAOYAZ
4: InChI=1/CHNO/c1-2-3/h1H
InChIKey=UXKUODQYLDZXDL-UHFFFAOYAL
5: InChI=1/CH2N2/c1-3-2/h1-2H
InChIKey=XILSUYCQFZFDIK-UHFFFAOYAR
6: InChI=1/C2H3N/c1-3-2/h1H,2H2
InChIKey=LSOWAYXKGAQDOG-UHFFFAOYAI
7: InChIInChIKey=DITLKQKHWHCNBT-UHFFFAOYAB
8: InChI=1/CH4N2/c1-3-2/h2-3H,1H2
InChIKey=SSRHHPGUPLMOHA-UHFFFAOYAA
9: InChI=1/C2H5N/c1-3-2/h3H,1-2H2
InChIKey=DASBPRRGHQBNKH-UHFFFAOYAE