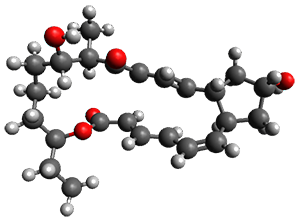
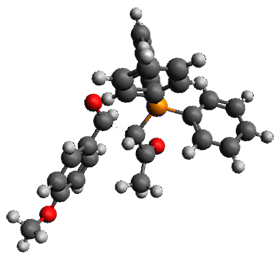
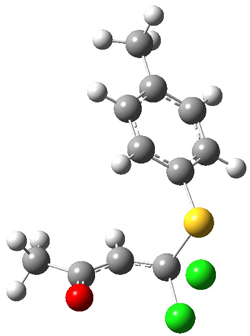
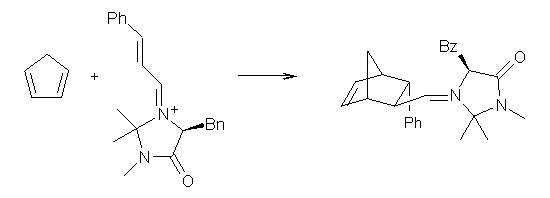
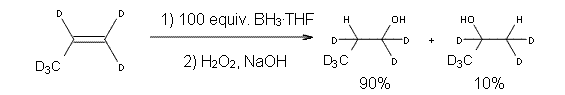Enzyme SpnF is implicated in catalyzing the putative [4+2] cycloaddition taking 1 into 3. Houk, Singleton and co-workers have now examined the mechanism of this transformation in aqueous solution but without the enzyme.¹ As might be expected, this mechanism is not straightforward.

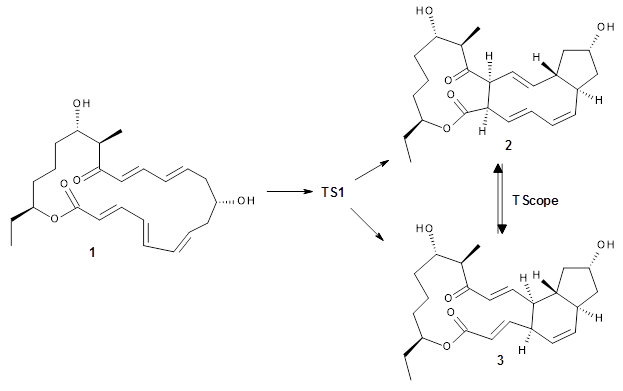
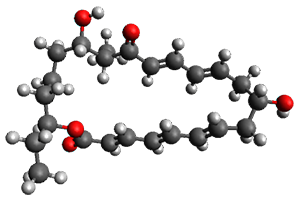
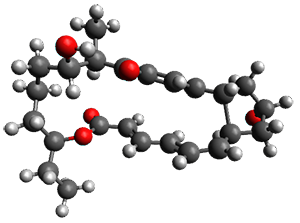
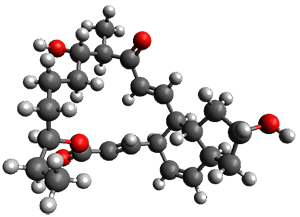
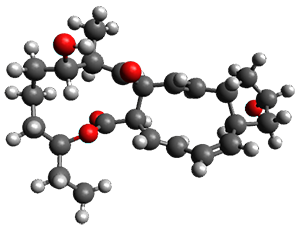
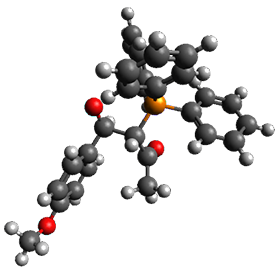
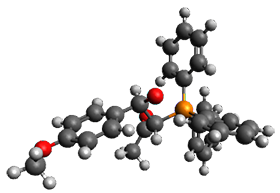
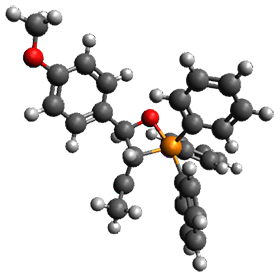
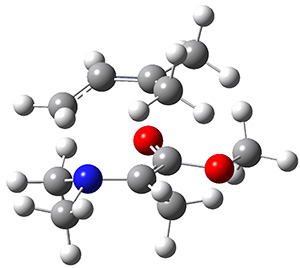
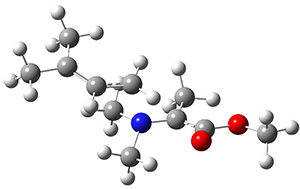
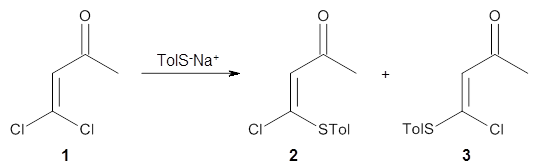
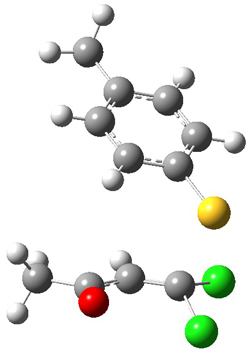
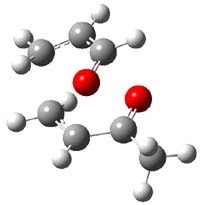
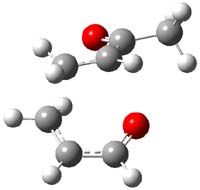
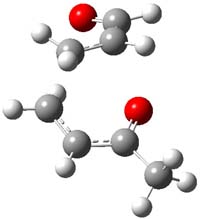
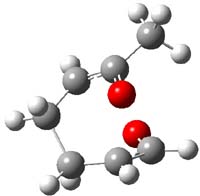
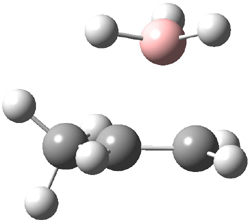
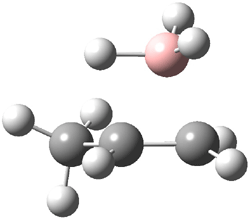
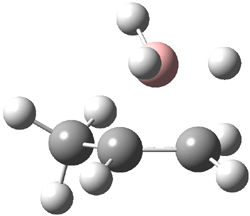
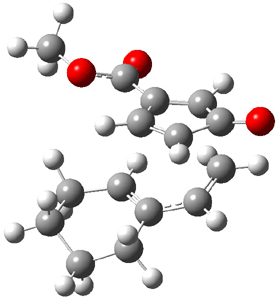
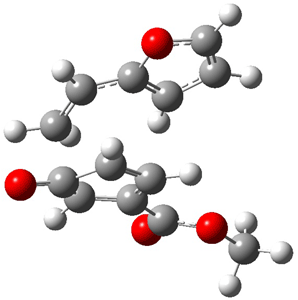
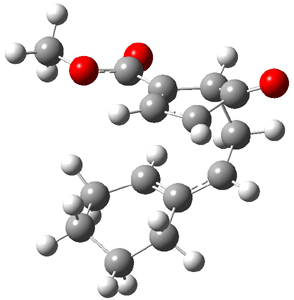
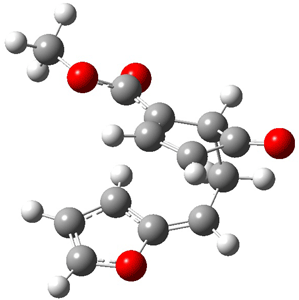
Reactant 1, transition states, and products 2 and 3 were optimized at SMD(H2O)/M06-2X/def2-TZVPP//B3LYP-D3(BJ)//6-31+G(d,p). Geometries and relative energies are shown in Figure 1. The reaction 1 → 2 is a formal [6+4] cycloaddition, and the reaction 1 → 3 is a formal [4+2] cycloaddition. Interestingly, only a single transition state could be located TS1. It is a bispericyclic TS (see Chapter 4 of my book), where these two pericyclic reaction sort of merge together. After TS1 is traversed the potential energy surface bifurcates, leading to 2 or 3. This is yet again an example of a single TS leading to two different products. (See the many posts I have written on this topic.) The barrier height is 27.6 kcal mol^-1, with 2 lying 13.1 kcal mol^-1 above 3. However, the steepest descent pathway from TS1 leads to 2. There is a second transition state TScope that describes a Cope rearrangement between 2 and 3. Using the more traditional TS theory description, 1 undergoes a [6+4] cycloaddition to form 2 which then crosses a lower barrier (TScope) to form the thermodynamically favored 3, which is the product observed in the enzymatically catalyzed reaction.

1 (0.0)
TS1 (27.6)
2 (4.0)	3 (-9.1)
(24.7)

Figure 1. B3LYP-D3(BJ)//6-31+G(d,p) optimized geometries and relative energies in kcal mol^-1.

Molecular dynamics computations were performed on this system by tracking trajectories starting in the neighborhood of TS1 on a B3LYP-D2/6-31G(d) PES. The results are that 63% of the trajectories end at 2, 25% end at 3, and 12% recross back to reactant 1, suggesting an initial formation ratio for 2:3 of 2.5:1. The reactions are very slow to cross through the “transition zone”, typically 2-3 times longer than for a usual Diels-Alder reaction (see this post).

Once again, we see an example of dynamic effects dictating a reaction mechanism. The authors pose a tantalizing question: Can an enzyme control the outcome of an ambimodal reaction by altering the energy surface such that the steepest downhill path from the transition state leads to the “desired” product(s)? The answer to this question awaits further study.

References

(1) Patel, A; Chen, Z. Yang, Z; Gutierrez, O.; Liu, H.-W.; Houk, K. N.; Singleton, D. A. “Dynamically
Complex [6+4] and [4+2] Cycloadditions in the Biosynthesis of Spinosyn A,” J. Amer. Chem. Soc. 2016, 138, 3631-3634, DOI: 10.1021/jacs.6b00017.

InChIs

1: InChI=1S/C24H34O5/c1-3-21-15-12-17-23(27)19(2)22(26)16-10-7-9-14-20(25)13-8-5-4-6-11-18-24(28)29-21/h4-11,16,18-21,23,25,27H,3,12-15,17H2,1-2H3/b6-4+,8-5+,9-7+,16-10+,18-11+/t19-,20+,21-,23-/m0/s1
InChIKey=JEKALMRMHDPSQK-ZTRRSECRSA-N

2: InChI=1S/C24H34O5/c1-3-19-8-6-10-22(26)15(2)23(27)20-12-11-17-14-18(25)13-16(17)7-4-5-9-21(20)24(28)29-19/h4-5,7,9,11-12,15-22,25-26H,3,6,8,10,13-14H2,1-2H3/b7-4-,9-5+,12-11+/t15-,16-,17-,18-,19+,20+,21-,22+/m1/s1
InChIKey=AVLPWIGYFVTVTB-PTACFXJJSA-N

3: InChI=1S/C24H34O5/c1-3-19-5-4-6-22(26)15(2)23(27)11-10-20-16(9-12-24(28)29-19)7-8-17-13-18(25)14-21(17)20/h7-12,15-22,25-26H,3-6,13-14H2,1-2H3/b11-10+,12-9+/t15-,16+,17-,18-,19+,20-,21-,22+/m1/s1
InChIKey=BINMOURRBYQUKD-MBPIVLONSA-N

If you hadn’t noticed, I am a big fan of the work that Dan Singleton is doing concerning the role of dynamics in discerning reaction mechanisms. Dan’s group has reported another outstanding study combining experiments, traditional QM computations, and molecular dynamics – this time on the Wittig reaction.¹

The key question concerning the mechanism is whether a betaine intermediate is accessed along the reaction (path A) or whether the reaction proceeds in a concerted manner (path B). Earlier computations had supported the concerted pathway (B).

Experimental determination of the heavy atom kinetic isotope effect was made for Reaction 1.

Reaction 1

Using the 6-31+G(2df,p) basis set, three different density functionals predict three different potential energy surfaces. With M06-2x, the surface indicates path A (stepwise), with the first step rate-limiting. B3P86 also predicts the stepwise reaction, but the second step is rate-limiting. The Lc-wPBE functional predicts a concerted reaction. Using these surfaces, they predicted the carbon isotope effect and compared it to the experimental values. The best agreement is with the M06-2x surface with a weighting of the vibrational energies of the two different TSs. The optimized structures of the two transition states, the betaine intermediate, and the product are shown in Figure 1.

TS1	Betaine
TS2	Product

Figure 1. M06-2x/6-31+G(2df,p) optimized geometry of the critical points of Reaction 1.

The agreement of the predicted and experimental KIE is not ideal. So, they performed molecular dynamics computations with the ONIOM approach using M06-2x/6-31G* for Reaction 1 and 53 THF molecules treated at PM3. 360 trajectories were begun in the region of the first transition state (TS1), and they can be organized into 4 groups. The first group (128 trajectories) are reactions that produce product. The second group (76 cases) form the C-C bond but then it ruptures and returns to reactant. The third group (82 cases) have an immediate recrossing back to reactant, and the last group (16 cases) takes product back to the first TS and then returns to product. The predicted KIE using this weighted MD results gives values in outstanding agreement with the experiments.

Of the first group, about 50% pass from TS1 to TS2 in less than 150 fs, or in other words look like a concerted path. But a good number of trajectories reside in the betaine region for 1-2 ps.

In contrast, trajectories initiated from the betaine with equilibrated THF molecules indicate a median of 600 ps to travel from TS1 to TS2 and do not resemble a concerted path.

They argue that this bimodal distribution is in part associated with a solvent effect. When the first TS is crossed the solvent molecules are not equilibrated about the solute, and 10-20% of the trajectories immediately pass through the betaine region due to “dynamic matching” where the entering motion matches with exiting over the second transition state. The longer trajectories result from improper dynamic matching, but faster motion in the solute than motion amongst the solvent needed to stabilize the betaine. So, not only do we need to be concerned about dynamic effects involving the reactants, we need to be concerned about dynamics associated with the solvent too!

References

(1) Chen, Z.; Nieves-Quinones, Y.; Waas, J. R.; Singleton, D. A. "Isotope Effects, Dynamic Matching, and Solvent Dynamics in a Wittig Reaction. Betaines as Bypassed Intermediates," J. Am. Chem. Soc. 2014, 136, 13122-13125, DOI: 10.1021/ja506497b.

While the [2-3]-sigmatropic rearrangement is well known and understood as allowed under the Woodward-Hoffmann rules, [1,2]-sigmatropic are much more rare, perhaps because they are forbidden by the same orbital symmetry arguments. It is perhaps surprising that these two rearrangements may sometimes be found in competition. Singleton has applied many of his tried-and-true techniques, namely, careful normal abundance kinetic isotope effect (KIE) analysis and molecular dynamics computations, to this problem.¹

Reaction 1 takes place exclusively through a [2,3]-rearrangement; the principle evidence is the lack of any crossover reaction. However, the slightly more substituted analogue shown in Reaction 2 gives rise to two products: that obtained from a [2,3]-rearrangement 6 and that obtained from a [1,2]-rearrangement 7.

The KIE for the rearrangement of 2 is large for the carbon breaking the bond with nitrogen, while it is small at the carbons that are forming the new bond. This becomes a metric for judging the transition state obtained with computations. With the computed TS and canonical variational transition state theory (VTST) including small curvature tunneling, the KIE can be computed from a computed structures and frequencies. This imposes a range of reasonable distances for the forming C-C bond of 2.6-2.9 Å – much longer that a typical distance in the TS of similar pericyclic reactions.

Crossover experiments for Reaction 2 are understood in terms of a reaction model whereby some fraction of the reactants undergo a concerted rearrangement to form 6, and 7 is formed by first breaking the C-N bond, forming two radicals, that either recombine right away or form isolated radicals that then collapse to product.

The interesting twist here is that one would expect two different transition states, one for the concerted process 8 and one to cleave the bond 9. Both do exist and are shown in Figure 1. However, VTST predicts that the concerted process should be 25-50 times faster than cleavage, and that does not match up with experiments. Amazingly, molecular dynamics trajectories started from the concerted TS 8 leads to cleavage about 20% of the time using UMO6-2X with a variety of basis sets. Thus, as Singleton has noted many times before, a single TS is crossed that leads to two different products! An argument based on entropy helps explain why the second (cleavage) pathway is viable.

8

9

Figure 1. UMO6-2x/6-31G* optimized structures of TS 8 and 9.

References

(1) Biswas, B.; Collins, S. C.; Singleton, D. A. "Dynamics and a Unified Understanding of Competitive [2,3]- and [1,2]-Sigmatropic Rearrangements Based on a Study of Ammonium Ylides," J. Am. Chem. Soc. 2014, 136, 3740-3743, DOI: 10.1021/ja4128289.

I think most organic chemists hold dear to their hearts the notion that selectivity is due to crossing over different transition states. Readers of my book and this blog know of the many examples where this notion simply is not true (see here). This post discusses yet another example taking place in a seemingly simple reaction.

Singleton has examined the nucleophilic substitution reaction of 1 with sodium tolylsulfide.¹ The mono substitution gives potentially two different stereoproducts 2 and 3. The experimental ratio of these products 2:3 is 81:19. (Note that things are a bit more complicated because disubstitution can also occur, but this has been factored into the product ratio.)

Based on previous literature, this reaction is likely to proceed in a concerted fashion, and so one might anticipate running computations to locate a transition state leading to 2 and a transition state leading to 3. In fact, Singleton finds six different TSs (the lowest energy TS 4 is shown in Figure 1), all within 2 kcal mol^-1 of each other at PCM(ethanol)/B3LYP/6-31+G**. However, the intrinsic reaction coordinate going forward from each of these six TSs leads solely to 2; no TS could be located that connects to 3! (Computations were also performed at PCM(ethanol)/M06-2x/6-31+G** which give very similar results.) Classical transition state theory would lead
one to conclude that only 2 should be formed, inconsistent with experiment.

4

5

Figure 1. PCM/B3LYP/6-31+G** optimized structures of TSs 4 and 5.

Furthermore, no intermediate could be located. This is consistent with a concerted mechanism. A second transition state was located which interconverts 2 and 3 with the involvement of a chloride – a sort of addition/rotation/elimination process. This TS 5 is also shown in Figure 1.

A direct dynamics study was performed, and 197 trajectories were computed. Of these, 185 trajectories went to product: 156 to 2 and 29 to 3, for a ratio of 84:16 – in amazing agreement with experiment! The product selectivity is due entirely to dynamic effects. In fact, it is one vibrational mode that dictates the product distribution. Essentially, the nature of the rotation about the C=C bond differentiates the eventual route, with a clockwise rotation leading always to 2 and a counterclockwise rotation leading about a third of the time to 3.

References

(1) Bogle, X. S.; Singleton, D. A. "Dynamic Origin of the Stereoselectivity of a Nucleophilic Substitution Reaction," Org. Lett., 2012, 14, 2528-2531, DOI: 10.1021/ol300817a.

InChIs

1: InChI=1S/C4H4Cl2O/c1-3(7)2-4(5)6/h2H,1H3
InChIKey=NXDUHPYJFYSBCT-UHFFFAOYSA-N

2: InChI=1S/C11H11ClOS/c1-8-3-5-10(6-4-8)14-11(12)7-9(2)13/h3-7H,1-2H3/b11-7-
InChIKey=NCXXSKTZGJETLW-XFFZJAGNSA-N

3: InChI=1S/C11H11ClOS/c1-8-3-5-10(6-4-8)14-11(12)7-9(2)13/h3-7H,1-2H3/b11-7+
InChIKey=NCXXSKTZGJETLW-YRNVUSSQSA-N

Once again the Singleton group reports experiments and computations that require serious reconsideration of our notions of reaction mechanisms.¹ In this paper they examine the reaction of dichloroketene with labeled cis-2-butene. With ¹³C at the 2 position of 2-butene, two products are observed, 1 and 1’, in a ratio of 1’:1 = 0.993 ± 0.001. This is the opposite what one might have imagined based on the carbonyl carbon acting as an electrophile.

The first interesting item is that B3LYP/6-31+G** fails to predict the proper structure of the transition state. It predicts an asymmetric structure 2, shown in Figure 1, while MPW1k/6-31+G**, M06, and MP2 predict a C_s transition structure 3. The C_s TS is confirmed by a grid search of M06-2x geometries with CCSD(T)/6-311++G88/PCM(CH₂Cl₂) energies.

2

3

Figure 1. Optimized TSs 2 (B3LYP/6-31+G**) and 3 (MPW1K/6-31+G**).

The PES using proper computational methods is bifurcating past TS 3, falling downhill to product 1 or 1’. Lying on the C_s plane is a second transition state that interconverts 1 and 1’. On such a surface, conventional transition state theory would predict equal amounts of 1 and 1’, i.e. no isotope effect! So they must resort to a trajectory study – which would be impossibly long if not for the trick of making the labeled carbon super-heavy – like ²⁸C,⁴⁴C, ⁷⁶C and ¹⁴⁰C and then extrapolating back to just ordinary ¹³C. These trajectories indicate a ratio of 1’:1 of 0.990 in excellent agreement with the experimental value of 0.993.

Interestingly, most trajectories recross the TS, usually by reaching into the region near the second TS. However, the recrossing decreases with increasing isotopic mass, and this leads to the isotope effect. It turns out the vibrational mode 3 breaks the C_s symmetry; movement in one direction along mode 3 has no mass dependence but in the opposite direction, increased mass leads to decreased recrossing – or put in another way, in this direction, increased mass leads more often to product.

But one can understand this reaction from a statistical point of view as well. If one looks at the free energy surface, there is a variational TS near 3, but then there is a second set of variational transition states (one leading to 1 and one to 1’) which are associated with the formation of the second C-C bond. In a sense there is an intermediate past 3 that leads to two entropic barriers, one on a path to 1 and one on the path to 1’. RRKM using this model gives a ratio of 0.992 – again in agreement with experiment! It is as Singleton notes “perplexing”; how do you reconcile the statistical view with the dynamical (trajectory) view? Singleton has no full explanation.

Lastly, they point out that a similar situation occurs in the organocatalyzed Diels-Alder reaction of MacMillan shown below.² (This reaction is also discussed in a previous post.) Now Singleton finds that the “substituent effects, selectivity, solvent effects, isotope effects and activation parameters” are all dictated by a second variational TS far removed from the conventional electronic TS.

References

(1) Gonzalez-James, O. M.; Kwan, E. E.; Singleton, D. A., "Entropic Intermediates and Hidden Rate-Limiting Steps in Seemingly Concerted Cycloadditions. Observation, Prediction, and Origin of an Isotope Effect on Recrossing," J. Am. Chem. Soc. 2012, 134, 1914-1917, DOI: 10.1021/ja208779k

(2) Ahrendt, K. A.; Borths, C. J.; MacMillan, D. W. C., "New Strategies for Organic Catalysis: The First Highly Enantioselective Organocatalytic Diels-Alder Reaction," J. Am. Chem. Soc. 2000, 122, 4243-4244, DOI: 10.1021/ja000092s.

InChIs

2-butene: InChI=1/C4H8/c1-3-4-2/h3-4H,1-2H3/b4-3-
InChIKey=IAQRGUVFOMOMEM-ARJAWSKDBO

Dichloroketene: InChI=1/C2Cl2O/c3-2(4)1-5
InChIKey=TVWWMKZMZALOFP-UHFFFAOYAY

1 (no isotope): InChI=1/C6H8Cl2O/c1-3-4(2)6(7,8)5(3)9/h3-4H,1-2H3/t3-,4+/m0/s1
InChIKey=BAEYWHUXGUIZSP-IUYQGCFVBH

Suppose a compound could exist in one of two ways: (a) a symmetrical structure like the bromonium cation A or (b) equilibrating structures that on a time-average basis appear symmetrical, like B. How would one differentiate between these two possibilities?

Saunders developed a method whereby the species is isotopically labeled and then examined by NMR.^1-3 For case B, isotopic labeling will desymmetrize the two structures and so the chemical shifts of what were equivalent nuclei will become (often quite) different. But the isotopic labeling of A, while breaking the symmetry, does so to a much lesser extent, and the chemical shit difference of the (former) equivalent nuclei will be similar.

Singelton has employed this concept using both experiment and theory for two interesting cases.⁴ For the bromonium cation 1, Ohta⁵ discovered that the ¹³C NMR chemical shifts differed by 3.61 ppm with the deuterium labels. This led Ohta to conclude that the bomonium cation is really two equilibrating structures. It should be noted that the DFT optimized structure has C_2v symmetry (a single symmetric structure). Singleton applied a number of theoretical methods, the most interesting being an MD simulation of the cation. A large number of trajectories were computed and then the NMR shifts were computed at each point along each trajectory to provide a time-averaged difference in the chemical shifts of 4.8 ppm. Thus 2 can express a desymmetrization even though the unlabled structure is symmetric. This desymmetrization is due to coupling of vibrational modes involving the isotopes.

The second example is phthalate 2. Perrin observed a large ¹⁸O chemical shift difference upon isotopic labeling of one of the oxygen atoms, suggesting equilibrating structures.⁶ An MD study of such a system would take an estimated 1500 processor-years. Instead, by increasing the mass of the label to ²⁴O, the trajectories could be computed in a more reasonable time, and this would result in an isotope effect that is 4 times too large. The oxygen chemical shifts of more the 2.5 million trajectory points were computed for the two labeling cases, and each again showed a large chemical shift difference even though the underlying structure is symmetrical.

Thus, isotopic labeling can desymmetrize a symmetrical potential energy surface.

References

(1) Saunders, M.; Kates, M. R., "Isotopic perturbation of resonance. Carbon-13 nuclear magnetic resonance spectra of deuterated cyclohexenyl and cyclopentenyl cations," J. Am. Chem. Soc., 1977, 99, 8071-8072, DOI: 10.1021/ja00466a061

(2) Saunders, M.; Telkowski, L.; Kates, M. R., "Isotopic perturbation of degeneracy. Carbon-13 nuclear magnetic resonance spectra of dimethylcyclopentyl and dimethylnorbornyl cations," J. Am. Chem. Soc., 1977, 99, 8070-8071, DOI: 10.1021/ja00466a060

(3) Saunders, M.; Kates, M. R.; Wiberg, K. B.; Pratt, W., "Isotopic perturbation of resonance. Carbon-13 nuclear magnetic resonance of 2-deuterio-2-bicyclo[2.1.1]hexyl cation," J. Am. Chem. Soc., 1977, 99, 8072-8073, DOI: 10.1021/ja00466a062

(4) Bogle, X. S.; Singleton, D. A., "Isotope-Induced Desymmetrization Can Mimic
Isotopic Perturbation of Equilibria. On the Symmetry of Bromonium Ions and Hydrogen Bonds," J. Am. Chem. Soc., 2011, 133, 17172-17175, DOI: 10.1021/ja2084288

(5) Ohta, B. K.; Hough, R. E.; Schubert, J. W., "Evidence for β-Chlorocarbenium and β-Bromocarbenium Ions," Organic Letters, 2007, 9, 2317-2320, DOI: 10.1021/ol070673n

(6) Perrin, C. L., "Symmetry of hydrogen bonds in solution," Pure Appl. Chem., 2009, 81, 571-583, DOI: 10.1351/PAC-CON-08-08-14.

Borden predicted measurable heavy-atom isotope effects in the ring opening of cyclopropylcarbinyl radical. In my blog post on this paper, I concluded with the line:

Borden hopes that experimentalists will reinvestigate this
problem (and hopefully confirm his predictions).

Well, in a recent paper where Borden collaborates with Singleton, these predictions are confirmed!¹

There is a sizable kinetic isotope effect for breaking the ring bond to a ¹²C over a bond to a ¹³C atom, up to 16% at -100 °C. The KIE predicted without including tunneling are dramatically below the experimental values, but incorporation of tunneling in the computated KIEs match up with experiment with an error no greater that 0.7%. The Arrhenius plot of ln KIE vs. 1/T shows enhanced isotope effects when tunneling is included, very nice agreement between the experimental and tunneling-corrected KIEs and curvature – all indicative of heavy atom tunneling. Lastly, the ring open product (1-butene) is the observed major product (62%) at -100 °C; the minor product is methylcyclopropane. In the absence of heavy-atom tunneling, 1-butene would be the minor product (28%).

References

(1) Gonzalez-James, O. M.; Zhang, X.; Datta, A.; Hrovat, D. A.; Borden, W. T.; Singleton, D. A. J. Am. Chem. Soc., 2010, 132, 12548-12549, DOI: 10.1021/ja1055593.

InChIs

Cyclopropylcarbonyl radical: InChI=1/C4H7/c1-4-2-3-4/h4H,1-3H2
InChIKey=RMCDUNHIVVEEDD-UHFFFAOYAR

1-butene: InChI=1/C4H8/c1-3-4-2/h3H,1,4H2,2H3
InChIKey=VXNZUUAINFGPBY-UHFFFAOYAZ

Dynamic effects rear up yet again in a seemingly simple reaction. Singleton has examined the Diels-Alder cycloaddition of acrolein with methyl vinyl ketone to give two cross products 1 and 2.¹ Upon heating the product mixture, 1 is essentially the only observed species. The retro-Diels-Alder is much slower than the conversion of 2 into 1. Using a variety of rate data, the best estimate for the relative formation of 1:2 is 2.5.

The eight possible transition states for this reaction were computed with a variety of methodologies, all providing very similar results. The lowest energy TS is TS3. A TS of type TS4 could not be found; all attempts to optimize it collapsed to TS3.

IRC computations indicate the TS3 leads to 1. The lowest energy TS that leads to 2 is TS6, but a second TS (TS5) lower in energy than TS6 also leads to 1. The other TS are still higher in energy. A Cope-type TS that interconverts 1 and 2 (TS7) was also located. The geometries of these TSs are shown in Figure 1.

TS3 (0.0)	TS5 (4.2)
TS6 (5.2)	TS7 (-0.4)

Figure 1. MP2/6-311+G** optimized geometries and relative energies (kcal mol^-1) of TS3-TS7.¹

Ordinary transition state theory cannot explain the experimental results – the energy difference between the lowest barrier to 1 (TS3) and to 2 (TS6) suggests a rate preference of over 700:1 for 1:2. But the shape of the potential energy surface is reminiscent of others that have been discussed in both my book (Chapter 7) and this blog (see my posts on dynamics) – a surface where trajectories cross a single TS but then bifurcate into two product wells.

To address the chemical selectivity on a surface like this, one must resort to molecular dynamics and examine trajectories. In their MD study of the 296 trajectories that begin at TS3 with motion towards product, 89 end at 1 and 33 end at 2, an amazingly good reproduction of experimental results! Interestingly, 174 trajectories recross the transition state and head back towards reactants. These recrossing trajectories result from “bouncing off” the potential energy wall of the forming C₄-C₅ bond.

In previous work, selectivity in on these types of surfaces was argued in terms of which well the TS was closer to. But analysis of the trajectories in this case revealed that a strong correlation exists between the initial direction and velocity in the 98 cm^-1 vibration – the vibration that corresponds to the closing of the second σ bond, the one between C₆-O₁ (forming 1), in the negative direction, and closing the C­₃-O₈ bond (forming 2) in the positive direction. Singleton argues that this is a type of dynamic matching, and it might be more prevalent that previously recognized.

References

(1) Wang, Z.; Hirschi, J. S.; Singleton, D. A., "Recrossing and Dynamic Matching Effects on Selectivity in a Diels-Alder Reaction," Angew. Chem. Int. Ed., 2009, 48, 9156-9159, DOI: 10.1002/anie.200903293

InChIs

1: InChI=1/C7H10O2/c1-6(8)7-4-2-3-5-9-7/h3,5,7H,2,4H2,1H3
InChIKey=AOFHZPHBPUYLAG-UHFFFAOYAJ

2: InChI=1/C7H10O2/c1-6-3-2-4-7(5-8)9-6/h3,5,7H,2,4H2,1H3
InChIKey=PLZQHPPETMMEED-UHFFFAOYAD

Singleton has again found a great example of a simple reaction that displays unmistakable non-statistical behavior.¹ The hydroboration of terminal alkenes proceeds with selectivity, preferentially giving the anti-Markovnikov product. The explanation for this selectivity is given in all entry-level organic textbooks – who would think that such a simple reaction could in fact be extraordinarily complex?

Reaction 1, designed to minimize the role of hydroboration involving higher order boron-hydrides (RBH₂ and R₂BH), the ratio of anti-Markovnikov to Markovinkov product is 90:10. Assuming that this ratio derives from the difference in the transition state energies leading to the two products, using transition state theory gives an estimate of the energy difference of the two activation barriers of 1.1 to 1.3 kcal mol^-1.

The CCSD(T)/aug-cc-pVDZ optimized structures of the precomplex between BH₃ and propene 1, along with the anti-Markovnikov transition state 2 and the Markovnikov transition state 3 are shown in Figure 2. The CCSD(T) energy extrapolated for infinite basis sets and corrected for enthalpy indicate that the difference between 2 and 3 is 2.5 kcal mol^-1. Therefore, transiitn state theory using this energy difference predicts a much greater selectivity of the anti-Markovnikov product, of about 99:1, than is observed.

1
2	3

Figure 1. CCSD(T)/aug-cc-pVDZ optimized geometries of 1-3.¹

In the gas phase, formation of the precomplex is exothermic and enthalpically barrierless. (A free energy barrier for forming the complex exists in the gas phase.) When a single THF molecule is included in the computations, the precomplex is formed after passing through a barrier much higher than the energy difference between 1 and either of the two transition states 2 or 3. (2 is only 0.8 kcal mol^-1 above 1 in terms of free energy.) So, Singleton speculated that there would be little residence time within the basin associated with 1 and the reaction might express non-statistical behavior.

Classical trajectories were computed. When trajectories were started at the precomplex 1, only 1% led to the Markovnikov product, consistent with transition state theory, but inconsistent with experiment. When trajectories were initiated at the free energy transition state for formation of the complex (either with our without a single complexed THF), 10% of the trajectories ended up at the Markovnikov product, as Singleton put it “fitting strikingly well with experiment”!

Hydroboration does not follow the textbook mechanism which relies on transition state theory. Rather, the reaction is under dynamic control. This new picture is in fact much more consistent with other experimental observations, like little change in selectivity with varying alkene substitution² and the very small H/D isotope effect of 1.18.³ Singleton adds another interesting experimental fact that does not jibe with the classical mechanism: the selectivity is little affect by temperature, showing 10% Markovnikov product at 21 °C and 11.2% Markovnikov product at 70 °C. Dynamic effect rears its ugly complication again!

References

(1) Oyola, Y.; Singleton, D. A., “Dynamics and the Failure of Transition State Theory in Alkene Hydroboration,” J. Am. Chem. Soc. 2009, 131, 3130-3131, DOI: 10.1021/ja807666d.

(2) Brown, H. C.; Moerikofer, A. W., “Hydroboration. XV. The Influence of Structure on the Relative Rates of Hydroboration of Representative Unsaturated Hydrocarbons with Diborane and with Bis-(3-methyl-2-butyl)-borane,” J. Am. Chem. Soc. 1963, 85, 2063-2065, DOI: 10.1021/ja00897a008.

(3) Pasto, D. J.; Lepeska, B.; Cheng, T. C., “Transfer reactions involving boron. XXIV. Measurement of the kinetics and activation parameters for the hydroboration of tetramethylethylene and measurement of isotope effects in the hydroboration of alkenes,” J. Am. Chem. Soc. 1972, 94, 6083-6090, DOI: 10.1021/ja00772a024.

Singleton has taken another foray into the murky arena of “dynamic effects”, this time with the aim of trying to provide some guidance towards making qualitative product predictions.¹ He has examined four different Diels-Alder reaction involving two diene species, each of which can act as either the diene or dienophile. I will discuss the results of two of these reactions, namely the reactions of 1 with 2 (Reaction 1) and 1 with 3 (Reaction 2).

In the experimental studies, Reaction 1 yields only 4, while reaction 2 yields both products in the ratio 6:7 = 1.6:1. Standard transition state theory would suggest that there are two different transition states for each reaction, one corresponding to the 4+2 reaction where 1 is the dienophile and the other TS has 1 as the dienophile. Then one would argue that in Reaction 1, the TS leading to 4 is much lower in energy than that leading to 5, and for Reaction 2, the TS state leading to 6 lies somewhat lower in energy than that leading to 7.

Now the interesting aspect of the potential energy surfaces for these two reactions is that there are only two transition states. The first corresponds to the Cope rearrangement between the two products (connecting 4 to 5 on the PES of Reaction 1 and 6 to 7 on the PES of Reaction 2). That leaves only one TS connecting reactants to products! These four TSs are displayed in Figure 1.

Reaction 1	Reaction 2
TS 12→45	TS 13→67
Cope TS 4→5	Cope TS 6→7

Figure 1. MPW1K/6-31+G** TSs on the PES of Reactions 1 and 2.¹

These transition states are “bispericyclic” (first recognized by Caramella²), having the characteristics of both possible Diels-Alder reactions, i.e. for Reaction 1 these are the [4π₁+2π₂] and [4π₂+2π₁]. What this implies is that the reactants come together, cross over a single transition states and then pass over a bifurcating surface where the lowest energy path (the IRC or reaction path) continues on to one product only. The second product, however, can be reached by passing over this same transition state and then following some other non-reaction path. This sort of surface is ripe for experiencing non-statistical behavior, or “dynamic effects”.

Trajectory studies were then performed to explore the product distributions. Starting from TS 12→45, 39 trajectories were followed: 28 ended with 4 and 10 ended with 5 while one trajectory recrossed the transition state. Isomerization of 5 into 4 is possible, and the predicted low barrier for this explains the sole observation of 4. For Reaction 2, of the 33 trajectories that originated at TS 13→67, 12 led to 6 and 19 led to 7. This distribution is consistent with the experimental product distribution of a slight excess of 7 over 6.

Once again we see here a relatively simple reaction whose product distribution is only interpretable using expensive trajectory computations, and the result leave little simplifying concepts to guide us in generalizing to other (related) systems. Singleton does provide two rules-of-thumb that may help prod us towards creating some sort of dynamic model. First, he notes that the geometry of the single transition state that “leads” to the two products can suggest the major product. The TS geometry can be “closer” to one product over the other. For example, in TS 12→45 the two forming C-C bonds that differentiate the two products are 2.95 and 2.99 Å, and the shorter distance corresponds to forming 4. In TS 13→67, the two C-C distances are 2.83 and 3.13 Å, with the shorter distance corresponding to forming 6. The second point has to do with the position of the second TS, the one separating the two products. This TS acts to separate the PES into two basins, one for each product. The farther this TS is from the first TS, the greater the selectivity.

As Singleton notes, neither of these points is particularly surprising in hindsight. Nonetheless, since we have so little guidance in understanding reactions that are under dynamic control, any progress here is important.

References

(1) Thomas, J. B.; Waas, J. R.; Harmata, M.; Singleton, D. A., "Control Elements in Dynamically Determined Selectivity on a Bifurcating Surface," J. Am. Chem. Soc. 2008, 130, 14544-14555, DOI: 10.1021/ja802577v.

(2) Caramella, P.; Quadrelli, P.; Toma, L., "An Unexpected Bispericyclic Transition Structure Leading to 4+2 and 2+4 Cycloadducts in the Endo Dimerization of Cyclopentadiene," J. Am. Chem. Soc. 2002, 124, 1130-1131, DOI: 10.1021/ja016622h

InChIs

1: InChI=1/C7H6O3/c1-10-7(9)5-2-3-6(8)4-5/h2-4H,1H3
InChIKey=XDEAUYSKQHEYSC-UHFFFAOYAM

2: InChI=1/C8H12/c1-2-8-6-4-3-5-7-8/h2,6H,1,3-5,7H2
InChIKey=SDRZFSPCVYEJTP-UHFFFAOYAI

3: InChI=1/C6H6O/c1-2-6-4-3-5-7-6/h2-5H,1H2
InChIKey=QQBUHYQVKJQAOB-UHFFFAOYAO

4: InChI=1/C15H18O3/c1-18-14(17)15-9-8-13(16)12(15)7-6-10-4-2-3-5-11(10)15/h6,8-9,11-12H,2-5,7H2,1H3/t1,12-,15+/m1/s1
InChIKey=IASNDVSMFFVIFJ-GDHFLIHABF

5: InChI=1/C15H18O3/c1-18-15(17)13-8-11-10(7-12(13)14(11)16)9-5-3-2-4-6-9/h5,8,10-12H,2-4,6-7H2,1H3
InChIKey=XOFSMKQRRVWZHS-UHFFFAOYAW

6: InChI=1/C13H12O4/c1-16-13(15)10-6-8-7(5-9(10)12(8)14)11-3-2-4-17-11/h2-4,6-9H,5H2,1H3
InChIKey=HTSLDILNKGZMHE-UHFFFAOYAH

7: InChI=1/C13H12O4/c1-16-12(15)13-6-4-10(14)8(13)2-3-11-9(13)5-7-17-11/h3-9H,2H2,1H3/t8-,9?,13-/m1/s1
InChIKey=URYPWPBQFGUBGW-KEJGKJRFBM