As mentioned in Chapter 2 of my book, many post-HF methods predict that planar benzene has an imaginary frequency, whereby out-of-plane bending leads to a lower energy structure.¹ This anomaly was suggested to result from intramolecular basis set incompleteness.

Asturiol, Duran and Salvador provide more evidence that the root cause is intramolecular basis set superposition error.² They propose an extension of the standard counterpoise correction, which has been widely applied to interacting molecules. They divide the molecule into small fragments and apply the counterpoise correction to these fragments. For benzene, they use C-H or (CH)₂ fragments. With this counterpoise correction, the imaginary frequency corresponding to an out-of-plane distortion is removed for all combinations of either MP2 or CISD with the 6-31+G*, 6-311G or 6-311++G basis sets. The planar indenyl anion, which is found to have 4 imaginary frequencies at MP2/6-311G, has no imaginary frequencies when the counterpoise correction is used.

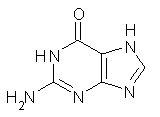
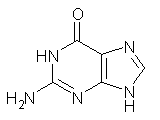
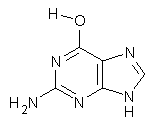
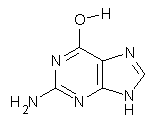
These authors have now shown that nucleic acid bases suffer from the same intramolecular superposition error.³ Uracil, thymine and guanine suffer from spurious imaginary frequencies with certain combinations of MP2 and Pople basis sets. However, all of these out-of-plane imaginary frequencies become real when the counterpoise correction is applied. The take-home message is to carefully mate the post-HF method and basis set combination – or else make the counterpoise correction!

References

(1) Moran, D.; Simmonett, A. C.; Leach, F. E.; Allen, W. D.; Schleyer, P. v. R.; Schaefer, H. F., III, "Popular Theoretical Methods Predict Benzene and Arenes To Be Nonplanar," J. Am. Chem. Soc. 2006, 128, 9342-9343, DOI: 10.1021/ja0630285

(2) Asturiol, D.; Duran, M.; Salvador, P., "Intramolecular basis set superposition error effects on the planarity of benzene and other aromatic molecules: A solution to the problem," J. Chem. Phys. 2008, 128, 144108, DOI: 10.1063/1.2902974

(3) Asturiol, D.; Duran, M.; Salvador, P., "Intramolecular Basis Set Superposition Error Effects on the Planarity of DNA and RNA Nucleobases," J. Chem. Theory Comput. 2009, 5, 2574-2581, DOI: 10.1021/ct900056u

Once more into the benzene dimer (see these previous posts: “Benzene dimer again“, “Benzene dimer“, “π-π stacking (part 2)“, “π-π stacking“)! Sherrill has published a detailed and impressive benchmark study of the benzene dimer in its three most important configurations: the D_6h stacked arrangement (1), the T-shaped arrangement (2) and the parallel displaced arrangement (3). ¹

First, they performed a careful extrapolation study to obtain accurate binding energies based on CCSD(T) with large basis sets. Then they compared the potential energy curves of the three configurations of benzene dimer obtained with this accurate method with those obtained with less computationally expensive methods. These alternates include RI-MP2, SCS-MP2 and a variety of different density functional. Their results are summarized in Table 1. The upshot is that the SCS-MP2 results are very similar to the much more expensive CCDS(T) values. And while the errors are a bit larger with the DFT methods, their performance is really quite good, especially given their dramatically lower costs. (Note that the “-D” indicates inclusion of Grimme’s dispersion correction term.) Particularly worth mentioning is the very fine performance of the MO6-2X functional.

Table 1. Binding energies (kcal mol^-1) of the three benzene dimers with different computational methods.

References

(1) Sherrill, C. D.; Takatani, T.; Hohenstein, E. G., "An Assessment of Theoretical Methods for Nonbonded Interactions: Comparison to Complete Basis Set Limit Coupled-Cluster Potential Energy Curves for the Benzene Dimer, the Methane Dimer, Benzene-Methane, and Benzene-H₂S" J. Phys. Chem. A 2009, ASAP, DOI: 10.1021/jp9034375

Here’s another fine paper from the Alonso group employing laser ablation molecular beam Fourier transform microwave spectroscopy coupled with computation to discern molecular structure. In this work they examine the low-energy tautomers of guanine.1 The four lowest energy guanine tautomers are shown in Figure 1. (Unfortunately, Alonso does not include the optimized coordinates of these structures in the supporting information – we need to more vigorously police this during the review process!) These tautomers are predicted to be very close in energy (MP2/6-311++G(d,p), and so one might expect to see multiple signals in the microwave originating from all four tautomers. In fact, they discern all four, and the agreement between the computed and experimental rotational constants are excellent (Table 1), especially if one applies a scaling factor of 1.004. Once again, this group shows the power of combined experiment and computations!

Figure 1. Four lowest energy (kcal mol^-1, MP2/6-311++G(d,p)) tautomers of guanine.

Table 1. Experimental and computed rotational constants (MHz) of the four guanine tautomers.

References

(1) Alonso, J. L.; Peña, I.; López, J. C.; Vaquero, V., "Rotational Spectral Signatures of Four Tautomers of Guanine," Angew. Chem. Int. Ed. 2009, 48, 6141-6143, DOI: 10.1002/anie.200901462

InChIs

Guanine: InChI=1/C5H5N5O/c6-5-9-3-2(4(11)10-5)7-1-8-3/h1H,(H4,6,7,8,9,10,11)/f/h8,10H,6H2
InChIKey=UYTPUPDQBNUYGX-GSQBSFCVCX

Shaik, Wu and Hiberty have proposed a third bond type, and they have a nice review article in Nature Chemistry.¹ Along with the long-standing concepts of the covalent bond and the ionic bond, they add a third category: the charge-shift bond.

The valence bond wavefunction for the diatomic A-B is written as

Ψ(VB) = c₁φ_cov(A-B) + c₂φ_ion(A⁺B^–) + c₃φ_ion(A^–X⁺)

Typically one of these terms dominates and we call the bond covalent if c₁ is the largest coefficient or ionic if either c₂ or c₃ is the largest term. The bond dissociation energy (D_e) is the difference in energy of the total VB wavefunction (above) and the energy of the separate radicals A^. and B^.. One can determine the energy due to just a single component of the total VB wavefunction. One might expect that for a covalent bond, the bond dissociation energy derived from just the c₁φ_cov(A-B) term would be close to D_e. For many covalent bonds this is true. However, Shaik and co-authors show a number of bonds where this is not true. For example, in the F-F bond, the covalent term is destabilizing. Rather, it is the resonance energy due to the mixing of the 3 VB terms that leads to bond formation. Shaik, Wu and Hiberty call this the “charge-shift bond”. They describe a number of examples of typically understood homonuclear and heteronuclear covalent bonds that are in fact charge-shift bonds, and an example of an ionic bond that really is charge-shift.

They argue that the charge-shift bond manifests as a consequence of the virial theorem. When an atom participates in a bond, its size gets smaller and this results in an increase in its kinetic energy. If the atom gets very small, then a substantial resultant change in the potential energy must occur, and this is the charge-shift bond. This also occurs in bonds involving atoms with many lone pairs; the lone-pair bond-weakening effect also causes a rise in kinetic energy that must be offset.

The authors speculate that many more examples of the charge-shift bond are waiting to be uncovered. It will be interesting if this concept catches hold and how quickly it will incorporated into general chemistry textbooks.

References

(1) Shaik, S.; Danovich, D.; Wu, W.; Hiberty, P. C., "Charge-shift bonding and its manifestations in chemistry," Nature Chem., 2009, 1, 443-449, DOI: 10.1038/nchem.327

Unusual potential energy surfaces are a theme of this blog and my book (see chapter 7). Examples might include bifurcations and valley inflection points and often lead to unusual dynamics. Tantillo has now reported a bifurcation on the PES for terpene synthesis, specifically the pathway for synthesis of abietadiene.¹

Tantillo discusses two possible cation rearrangement pathways. The first is pretty ordinary, but in the second, the precursor cation 1 can rearrange through either of two transition states 2a or 2b (Scheme 1). The IRC computation from 2a connects back to 1, but in the forward direction it connects to another transition state 3. This TS (3) connects products 4 and 5. These structures are drawn in Figure 1.

Thus, the potential energy surface displays a bifurcation, and one might expect unusual dynamic effects to operate.

Scheme 1

2a	2b
3

Figure 1. B3LYP/6-31+G(d,p) optimized transition structures of 2-3.¹

References

(1) Hong, Y. J.; Tantillo, D. J., "A potential energy surface bifurcation in terpene biosynthesis," Nature Chem. 2009, 1, 384-389 DOI: 10.1038/nchem.287.

One of the great longstanding dreams of synthetic and theoretical organic chemists is to prepare a stable molecule containing a pentacoordinate carbon atom. Bickelhaupt and co-workers propose a novel series of compounds that hint that this might be possible.¹

Their attack is to first find a CR₃ radical that is stable in its planar form. The nitrile group perfectly satisfies this goal. Next they look at the series of compounds X-C(CN)₃-X^– (1) where X is a halogen, searching for a stable D_3h structure. This is found with the halogens: Br, I, and At, at the ZORA-OLYP/TZ2P level. Seems like case closed, except that inspection of the supporting materials shows that the nature of the D_3h structure is sensitive to computational method. So, with the larger basis set ZORA-OLYP/QZ4P or with ZORA-OPBE/TZ2P, only the I and At compounds are local D_3h minima. And with ZORA-M06/TZ2P, only the At compound is a local minimum. The authors do mention these points at the end of the article. So, what we have here is a tantalizing suggestion for how to prepare a hypercoordinate carbon species, but further computational (and experimental) work is clearly needed.

1: X = F, Cl, Br, I, At

References

(1) Pierrefixe, S. C. A. H.; van Stralen, S. J. M.; van Strale, J. N. P.; Guerra, C. F.; Bickelhaupt, F. M., "Hypervalent Carbon Atom: "Freezing" the S_N2 Transition State," Angew. Chem. Int. Ed., 2009, 48, 6469-6471, DOI: 10.1002/anie.200902125

InChIs

1(F): InChI=1/C4F2N3/c5-4(6,1-7,2-8)3-9/q-1, InChIKey=LBDHZXPWKBFYBC-UHFFFAOYAX

1(Cl): InChI=1/C4Cl2N3/c5-4(6,1-7,2-8)3-9/q-1, InChIKey=NMFGEVWEEWBFSS-UHFFFAOYAU

1(Br): InChI=1/C4Br2N3/c5-4(6,1-7,2-8)3-9/q-1, InChIKey=FHKJQJBDHAEQES-UHFFFAOYAC

1(I): InChI=1/C4I2N3/c5-4(6,1-7,2-8)3-9/q-1, InChIKey=FWKBAUUEXUSUNH-UHFFFAOYAO

1(At): InChI=1/C4At2N3/c5-4(6,1-7,2-8)3-9/q-1, InChIKey=BJQBFKCUAROAAS-UHFFFAOYAK

Nature has a special feature on data sharing, including an editorial and commentaries advocating for both pre- and post-publication of data. I have long been an advocate of data sharing, especially in the post-publication sense (I would argue this is really concurrent-publication data sharing) – and one can read my latest commentary in the Journal of Cheminformatics (DOI: 10.1186/1758-2946-1-2.

Data sharing has been slow in chemistry. Peter Murray-Rust and Henry rzepa have been the major advocates for enhanced publication – see their blogs (PMR and HSR) and lots of publications. Tony Williams (blog) has been advocating for more deposition of data within ChemSpider, and some positive response have occurred. But journals and AUTHORS have been slow to change – supporting materials is often lacking important information and is rarely of useful form – and I consider pdf to be just a slice above “non-useful”. We need to continue to evangelize this issue!

Bond-stretch isomerism refers to isomers that differ simply in their bond lengths. Seppelt and coworkers suggests that the hexafluorobenzne radical cation C₆F₆^.+ exhibits bond-stretch isomerism.¹

The oxidized C₆F₆ with O₂⁺SbF₁₁^– and obtained C₆F₆^.+Sb­2F₁₁^– as a crystalline solid. X-ray diffraction identified 2 structures. B3LYP/TZPP computations confirmed the identity of two isomers, a “quinoid” form 1 and a “bisallyl” form 2, shown in Figure 1. The two structures are nearly degenerate, with 1 predicted to be 0.09 kcal mol^-1 more stable than 2. The computed two unique C-C bond lengths are 1.371 and 1.427 Å in 1 and 1.449 and 1.389 Å in 2, and these distance agree well with the X-ray experimental values.

1 – quinoid	2 – bisallyl

Figure 1. UB3LYP/6-311+G(d) optimized structures of 1 and 2. Note once again the article and supporting materials lacked the full description of these structures!)

The potential energy surface in the neighborhood of these two isomers is like that of a sombrero. The two isomers lie in the circular trough and movement around this trough is nearly flat. The peak of the sombrero is the D_6h structure, which is a transition state interconverting 1 and 2, with a barrier of 3 kcal mol^-1.

1 and 2 are clear examples of bond-stretch isomerism, though it is likely that the complexation with the counter ion is what freezes out the rapid interconversion of the two.

References

(1) Shorafa, H.; Mollenhauer, D.; Paulus, B.; Seppelt, K., "The Two Structures of the Hexafluorobenzene Radical Cation C₆F₆^.+," Angew. Chem. Int. Ed. 2009, 48, 5845-5847, DOI: 10.1002/anie.200900666

The octaphyrin 1 has been prepared and its crystal structure and electronic circular dichroism (ECD) spectra reported.¹ The x-ray structure identified the compound as having the M,M helical structure. The optical rotation however could not be determined.

Rzepa now reports the computed ECD spectrum and optical activity of 1 and some related compounds.² These computed spectra were obtained using TD0DFT with the B3LYP/6-31G(d) method with the CPCM treatment of the dichloromethane solvent. (The structure of 1 and other computed properties are available from the enhanced web table that Rzepa has deposited with the article (here). Once again this material seems to be available only to subscribers! My repeated discussions with ACS Pubs people that these “web objects” should be treated as data and not as copyrighted materials have fallen on deaf ears.) The computed ECD spectrum matches nicely with the experimental one, except that the signs at 570 and 620 nm are opposite. Rzepa suggests that either the compound is really of P,P configuration or the authors of experimental work have erroneously switched their assignments.

The computed value of [α]_D of 1 is about -4000 °, with the negative sign in agreement with the sign for [α]_D of M-hexahelicene. However, what is truly fantastic is the magnitude of the optical activity of the dication of 1 produced by loss of 2 electrons. This dication should be aromatic and it is predicted to have [α]₁₀₀₀ = -31597°!

References

(1) Werner, A.; Michels, M.; Zander, L.; Lex, J.; Vogel, E., ""Figure Eight" Cyclooctapyrroles: Enantiomeric Separation and Determination of the Absolute Configuration of a Binuclear Metal Complex," Angew. Chem. Int. Ed. 1999, 38, 3650-3653, DOI: 10.1002/(SICI)1521-3773(19991216)38:24<3650::AID-ANIE3650>3.0.CO;2-F

(2) Rzepa, H. S., "The Chiro-optical Properties of a Lemniscular Octaphyrin," Org. Lett. 2009, 11, 3088–3091DOI: 10.1021/ol901172g

I have written many posts on the use of computed NMR shifts as a tool for determining molecular structure, especially stereochemistry. All of these methods rely upon computing a bunch of alternative structures and then identifying the one whose chemical shifts (¹H and/or ¹³C) match up best with experiment. Many people have been interested in the first part of this process – the “computing a bunch of alternative structures” – testing the QM method, the basis set, the selection of conformation(s), and the method for computing chemical shifts. The subject of this post is the notion of “matching up best” and comes from of a recent article by Jonathan Goodman.¹

So in the typical procedure for deciding which structure (of many) best accounts for the experimental NMR spectra, the computed NMR shifts (and perhaps coupling constants) are compared to the experimental data. This comparison is done often by simply examining the correlation coefficient r between the experimental and calculated shifts. Some have used the mean absolute error between the computed and experimental shifts. Others have employed a corrected mean absolute error where scaled chemical shifts are first obtained from the plot of the calculated vs. experimental shifts, and then finding the average of the differences between these scaled shifts and the experimental ones.

Goodman suggests that oftentimes what is of interest is not really the chemical shifts of a compound but rather identifying the structure of diastereomers, and then it’s really the differences in the chemical shifts of pairs of diastereomers that are really critical in identifying which one is which. Using Goodman’s notation, suppose you have experimental NMR data on diastereomers A and B and the computed NMR shifts for structures a and b. The key is deciding does A correlate with a or b and the same for B. Goodman proposes three variants on how to compare the chemical shift differences, but I’ll show just the first, which he calls CP1. Define Δ_expⁱ as the differences in the experimental chemical shifts of the two diastereomers for nucleus i: Δ_exp = δ_Aⁱ – δ_Bⁱ and a similar definition for the differences in the computed shifts: Δ_calc = δ_aⁱ – δ_bⁱ. CP1 is then defined as Σ (Δ_exp/Δ_calc)/Σ (Δ_exp)² where each sum is over the nuclei i. Goodman shows in a number of examples (some are shown below) that CP1 and its variants provides an excellent measure of when a computed structure’s chemical shifts agree with the experimental values, along with a means for noting the confidence in that assignment. These CP measures provide significantly better measures of agreement that the ones previous utilized, providing a real confidence level in assessing the quality of the prediction. I strongly urge all who are interested in the use of computed NMR in determining molecular structures to read this paper and consider adopting this approach.

References

(1) Smith, S. G.; Goodman, J. M., "Assigning the Stereochemistry of Pairs of Diastereoisomers Using GIAO NMR Shift Calculation," J. Org. Chem. 2009, 74, 4597-4607, DOI: 10.1021/jo900408d