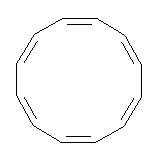
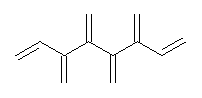
Conjugated alkenes have played a major role in conceptualizing organic chemistry. Linear and cyclic unbranched conjugated alkenes have been well studied; the latter class comprising the aromatic and antiaromatic annulenes. The cyclic branched conjugate alkenes are known as radialenes and have been subject of some study. But the last category, the linear branched conjugated alkenes have been overlooked. Paddon-Row and Sherburn¹ now report a general synthetic method for preparing these species, which they call dendralenes, see Scheme 1.

Scheme 1. Classes of conjugated alkenes

The dendralenes fall into two groups – those with an odd number of double bonds and those with an even number. While the UV/Vis absorption maximum redshifts with increasing length, the molar extinctions coefficients are relatively constant for the odd denralenes but it increases by about 10,000 within the even dendralene family. The Diels-Alder chemistry is even more distinctive: the odd dendralenes react rapidly with an electron deficient dienophile (N-methylmaleimide), with rates decreasing slightly with increasing size, but the even dendralenes are significantly more sluggish.

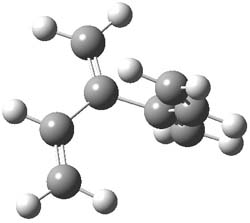
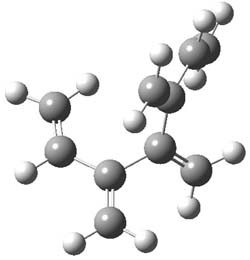
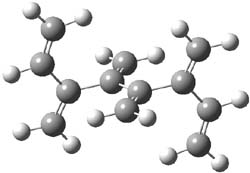
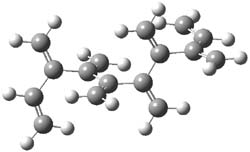
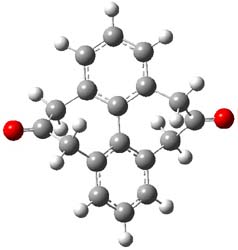
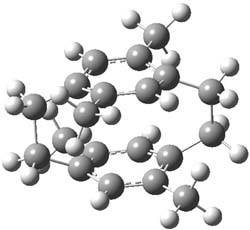
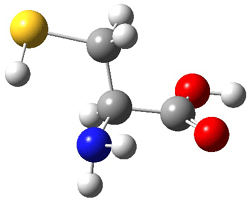
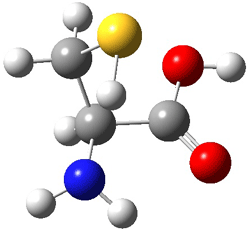
The optimized B3LYP/6-31G(d) geometries of the lowest energy conformers of the [3]- to [8]dendralenes are shown in Figure 1. There are three types of butadiene fragments present in these structures: (a) near planar s-trans arrangement, (b) near perpendicular arrangement of the two double bonds, and (c) ­s-cis arrangement with the dihedral angle about 40°. The even dendralenes have only the first two type: alternating planar butadiene fragment that are more-or-less orthogonal to each other. The odd dendralenes all have at least one s-cis arrangement. Paddon-Row and Sherburn suggest that since the s-cis arrangement is necessary for the diene component of the Diels-SAlder reaction, the odd dendralenes are more reactive than the even ones since they have this arranegement in their ground state conformations, while the even dendralenes will have to react out of a higher energy conformation. This is a nice explanation readily formulated from simple computations.

[3]dendralene	[4]dendralene
[5]dendralene	[6]dendralene
[7]dendralene	[8]dendralene

Figure 1. B3LYP/6-31G(d) optimized structures of [3]- to [8]dendralene.¹

References

(1) Payne, A. D.; Bojase, G.; Paddon-Row, M. N.; Sherburn, M. S., "Practical Synthesis of the Dendralene Family Reveals Alternation in Behavior," Angew. Chem. Int. Ed. 2009, 48, 4836-4839, DOI: 10.1002/anie.200901733

InChIs

[3]dendralene: InChI=1/C6H8/c1-4-6(3)5-2/h4-5H,1-3H2
InChIKey=VXBVLYQDVVHAHZ-UHFFFAOYAS

[4]dendralene: InChI=1/C8H10/c1-5-7(3)8(4)6-2/h5-6H,1-4H2
InChIKey=DMCINEDFOKMBFI-UHFFFAOYAV

[5]dendralene: InChI=1/C10H12/c1-6-8(3)10(5)9(4)7-2/h6-7H,1-5H2
InChIKey=XEZCEXNNZGLEHB-UHFFFAOYAM

[6]dendralene: InChI=1/C12H14/c1-7-9(3)11(5)12(6)10(4)8-2/h7-8H,1-6H2
InChIKey=RBABOPLFRQKABD-UHFFFAOYAA

[7]dendralene: InChI=1/C14H16/c1-8-10(3)12(5)14(7)13(6)11(4)9-2/h8-9H,1-7H2
InChIKey=ZIBYAXDRKFGSBF-UHFFFAOYAH

[8]dendralene: InChI=1/C16H18/c1-9-11(3)13(5)15(7)16(8)14(6)12(4)10-2/h9-10H,1-8H2
InChIKey=YWPORNAHEZCVCQ-UHFFFAOYAR

Jan Martin and his group at the Weizmann Institute continue to push the envelope in developing a computational rubric that produces computed energies with experimental accuracy. Their latest attempt tries to balance off computational accuracy with performance, and they propose the W3.2lite composite method,¹ which includes, among other things, an empirical correction for including triples and quadruples configurations.

Amongst the test molecules they discuss are the benzynes (the ortho, meta, and para diradicals) discussed at great length in Chapter 4.4 of my book. The W3.2lite estimate heats of formations are 112.06 ± 0.5, 125.06 ± 0.5, and 139.03 ± 0.5 kcal mol^-1 for the o-, m-, and p-benzyne, respectively. This compares with the experimental² estimates of 108.8 ± 3, 124.1 ± 3.1, and 139.5 ± 3.3 kcal mol^-1, respectively. This demonstrates nice agreement between the computed and experimental values. A similar sized difference is obtained for the singlet-triplet gap of p-benzyne: 5.4 ± 0.6 with W3.2lite and 3.8 ± 0.5 kcal mol^-1 estimate from ultraviolet photoelectron spectroscopy.³

References

(1) Karton, A.; Kaminker, I.; Martin, J. M. L., "Economical Post-CCSD(T) Computational Thermochemistry Protocol and Applications to Some Aromatic Compounds," J. Phys. Chem. A 2009, DOI: 10.1021/jp900056w.

(2) Wenthold, P. G.; Squires, R. R., "Biradical Thermochemistry from Collision-Induced Dissociation Threshold Energy Measurements. Absolute Heats of Formation of ortho-, meta-, and para-Benzyne," J. Am. Chem. Soc. 1994, 116, 6401-6412, DOI: 10.1021/ja00093a047.

(3) Wenthold, P. G.; Squires, R. R.; Lineberger, W. C., "Ultraviolet Photoelectron Spectroscopy of the o-, m-, and p-Benzyne Negative Ions. Electron Affinities and Singlet-Triplet Splittings for o-, m-, and p-Benzyne," J. Am. Chem. Soc. 1998, 120, 5279-5290, DOI: 10.1021/ja9803355.

InChIs

o-benzyne: InChI=1/C6H4/c1-2-4-6-5-3-1/h1-4H
InChIKey=KLYCPFXDDDMZNQ-UHFFFAOYAO

m-benzyne: InChI=1/C6H4/c1-2-4-6-5-3-1/h1-3,6H
InChIKey=MDEXXEPHAKMVNO-UHFFFAOYAG

p-benzyne: InChI=1/C6H4/c1-2-4-6-5-3-1/h1-2,5-6H
InChIKey=AIESRBVWAFETPR-UHFFFAOYAI

I have written a number of blog posts that deal with the computation of optical activity. Trindle and Altun have now reported TD-DFT computations of circular dichroism of high-symmetry molecules.¹ The employ either B3LYP (with a variety of basis sets, the largest being 6-311++G(2d,2p)) and SOAP/ATZP. For a number of the high symmetry molecules (two examples are shown in Figure 1), the two methods differ a bit in their predictions of the first excited state, with SOAP typically predicting a red shift relative to the B3LYP. However, both methods general give the same sign of the CD signals and their line shapes are similar.

1	2

Figure 1. B3LYP/6-31G(d) optimized structures of 1 and 2 (again due to incomplete supporting materials, I reoptimized these structures)

References

(1) Trindle, C.; Altun, Z., "Circular dichroism of some high-symmetry chiral molecules: B3LYP and SAOP calculations " Theor. Chem. Acc. 2009, 122, 145-155, DOI: 10.1007/s00214-008-0494-8.

InChIs

1: InChI=1/C18H14O2/c19-15-7-11-3-1-4-12-8-16(20)10-14-6-2-5-13(9-15)18(14)17(11)12/h1-6H,7-10H2
InChIKey=DYZSIUYFWKNLHS-UHFFFAOYAB

2: InChI=1/C20H24/c1-13-9-18-7-8-20-12-15(3)19(11-16(20)4)6-5-17(13)10-14(18)2/h9-12H,5-8H2,1-4H3
InChIKey=JTMLLDPOLFRPGJ-UHFFFAOYAC

I (0.0)	II (4.79)
III (5.81)	IV (5.95)

Figure 1. MP2(FC)/aug-cc-pV(T+d)Z optimized geometries and focal point relative energies (kJ mol^-1) of the four lowest energy conformers of cysteine.¹

The three lowest energy structures found here match up with the lowest two structures found by Alonso and the energy differences are also quite comparable: 4.79 kJ and 5.81 mol^-1 with the focal point method 3.89 and 5.38 kJ mol^-1 with MP4/6-311++G(d,p)// MP2/6-311++G(d,p). So the identification of the cysteine conformers made by Alonso remains on firm ground.

References

(1) Wilke, J. J.; Lind, M. C.; Schaefer, H. F.; Csaszar, A. G.; Allen, W. D., "Conformers of Gaseous Cysteine," J. Chem. Theory Comput. 2009, DOI: 10.1021/ct900005c.

(2) Sanz, M. E.; Blanco, S.; López, J. C.; Alonso, J. L., "Rotational Probes of Six Conformers of Neutral Cysteine," Angew. Chem. Int. Ed. 2008, 4, 6216-6220, DOI: 10.1002/anie.200801337

InChIs

Cysteine:
InChI=1/C3H7NO2S/c4-2(1-7)3(5)6/h2,7H,1,4H2,(H,5,6)/t2-/m0/s1
InChIKey: XUJNEKJLAYXESH-REOHCLBHBU

The Kim and Osuka groups have reported another Möbius aromatic porphyrin, 1, a 28 π-electron system.¹ This hexaporphyrin is produced without the need for low temperature, complexation with a metal or protonation (see this post for a discussion of their earlier work). The x-ray crystal structure shows the Möbius twist, and the ¹H NMR shifts of the interior protons at 2.22 and 1.03 ppm. B3LYP/6-31G** computations indicate a NICS value at the center of the molecule of -11.8 ppm. These are consistent with aromatic behavior.

References

(1) Tokuji, S.; Shin, J.-Y.; Kim, K. S.; Lim, J. M.; Youfu, K.; Saito, S.; Kim, D.; Osuka, A., "Facile Formation of a Benzopyrane-Fused [28]Hexaphyrin That Exhibits Distinct Möbius Aromaticity," J. Am. Chem. Soc. 2009, 131, 7240-7241, DOI: 10.1021/ja902836x.

InChIs

1: InChIKey=YGJLOPZWRVMFIJ-XFAHNSIYBC

Here are two nice examples of the use of computed spectra in identifying the structure of large molecules.

Castle and co-workers describe the synthesis of what they hoped would be runanine 1.¹ However, after they had completed their synthesis, the ¹H NMR spectrum of their product differed significantly from that of runanine. Further the optical rotation of 1 is -400, while that of their product is -34. Speculating on what might be the product they came up with 4 alternative structures 2-5. The ¹³C NMR of 1-5 were then computed by optimizing the structures at mPW1PW91/6-31G* followed by a GIAO computation at mPW1PW91/aug-cc-pVDZ with PCM (solvent is chloroform). The differences between the computed chemical shifts for 1-5 and the experimental shifts of the obtained product are summarized in Table 1. The authors conclude that their product is 5, a compound they name isorunanine.

Table 1. Average difference and maximum difference between the computed and experimental ¹³ C chemical shifts (ppm).

The authors also report the rather poor agreement between the computer spectrum of 6 and the experimental spectrum in benzene. Unfortunately, not enough details are provided to really determine where errors might be occurring. For example, there is no indication of examining multiple conformations (and those methoxy groups can rotate along with the inversion at the amine). Once again, the supporting materials, while extensive in terms of experimental NMR spectra, contain no details of the computed structures.

The structure of hypurticin 6 was determined using a comparison of computed coupling constants.² Here the authors first assumed that four possible stereoisomers are possible 6a-d, given that the other stereocenters were determined unambiguously by experiment and biogenesis considerations. B3LYP/6-31G(d) optimization of a restricted set of conformations led to the lowest energy conformer. The coupling constants computed for these four structures indicated the closet agreement between the computed constants of 6a with experimental values. An exhaustive search of the conformational space of each of these diastereomers at B3LYP/DGDZVP followed by Boltzmann weighting of the coupling constants confirmed that 6a is the structure of hypurticin.

References

(1) Nielsen, D. K.; Nielsen, L. L.; Jones, S. B.; Toll, L.; Asplund, M. C.; Castle, S. L., "Synthesis of Isohasubanan Alkaloids via Enantioselective Ketone Allylation and Discovery of an Unexpected Rearrangement," J. Org. Chem. 2009, 74, 1187-1199, DOI: 10.1021/jo802370v.

(2) Mendoza-Espinoza, J. A.; Lopez-Vallejo, F.; Fragoso-Serrano, M.; Pereda-Miranda, R.; Cerda-Garcia-Rojas, C. M., "Structural Reassignment, Absolute Configuration, and Conformation of Hypurticin, a Highly Flexible Polyacyloxy-6-heptenyl-5,6-dihydro-2H-pyran-2-one," J. Nat. Prod. 2009, 72, 700-708, DOI: 10.1021/np800447k.

Torquoselectivity rules (discussed in Chapter 3.5 of my book) indicate that 3-phenylcyclobutene will ring-open to give the outward rotated product (Reaction 1). Houk and Tang report a seeming contradiction, namely the ring opening of 1 gives only the inward product 3 (Reaction 2).¹

B3LYP/6-31G* computations on the ring-opening of 4 indicate that the activation barrier for the outward path (leading to 5) is nearly 8 kcal mol^-1 lower than the barrier for the inward path (leading to 6, see Reaction 3). This is consistent with torquoselectivity rules, but what is going on in the experiment?

In the investigation of the isomerization of the outward to inward pathway, they discovered a low-energy pyran intermediate 7. This led to the proposal of the mechanism shown in Reaction 3. The highest barrier is for the electrocyclization that leads to the outward product 5. The subsequent barriers – the closing to the pyran 7 and then the torquoselective ring opening to 6 –  are about than 13 kcal mol^-1 lower in energy than for the first step. The observed product is the thermodynamic sink. And the nice thing about this mechanism is that torquoselection is preserved.

References

(1) Um, J. M.; Xu, H.; Houk, K. N.; Tang, W., "Thermodynamic Control of the Electrocyclic
Ring Opening of Cyclobutenes: C=X Substituents at C-3 Mask the Kinetic Torquoselectivity," J. Am. Chem. Soc. 2009, 131, 6664-6665, DOI: 10.1021/ja9016446.

InChIs

4: InChI=1/C16H16O6/c1-20-13(17)11-9-16(14(18)21-2,15(19)22-3)12(11)10-7-5-4-6-8-10/h4-9,12H,1-3H3
InChIKey=VBOGEHVOAGDMNG-UHFFFAOYAR

5: InChI=1/C16H16O6/c1-20-14(17)12(9-11-7-5-4-6-8-11)10-13(15(18)21-2)16(19)22-3/h4-10H,1-3H3/b12-9-
InChIKey=PZRWKBUUAFMPBC-XFXZXTDPBF

6: InChI=1/C16H16O6/c1-20-14(17)12(9-11-7-5-4-6-8-11)10-13(15(18)21-2)16(19)22-3/h4-10H,1-3H3/b12-9+
InChIKey=PZRWKBUUAFMPBC-FMIVXFBMBS

7: InChI=1/C16H16O6/c1-19-14(17)11-9-12(15(18)20-2)16(21-3)22-13(11)10-7-5-4-6-8-10/h4-9,13H,1-3H3/t13-/m0/s1
InChIKey=QSJZITDSTPMCEM-ZDUSSCGKBG

Back when I was first learning ab initio methods in Cliff Dykstra’s lab, I played a bit with the post-HF method CEPA (couple electron pair approximation). This method fell out of favor over the years with the rise of MP theory and then with DFT. Now, Neese and Grimme and co-workers are resurrecting it.¹ Their Accounts article provides a series of tests of CEPA/1 against benchmark computations (typically CCSD(T)) and lo and behold, CEPA performs remarkably well! It bests B3LYP (no surprise there), B2LYP and MP2 in virtually every category, ranging from reaction energies, hydrogen bond energies, van der Waals interaction energies, and activation barrier heights. As an example, for the isomerization energy of toluene to norbornadiene, CCSD(T) estimates the energy is 42.79 kcal mol^-1. B3LYP does miserably, with an error of nearly 14 kcal mol^-1, but the CEPA/1 estimate is off by only 0.04 kcal mol^-1. Since the computational time of CEPA/1 is competitive with MP2, the authors conclude that CEPA/1 is well-worth reinvestigating as an alternative post-HF methodology.

References

(1) Neese, F.; Hansen, A.; Wennmohs, F.; Grimme, S., "Accurate Theoretical Chemistry with Coupled Pair Models," Acc. Chem. Res. 2009, 42, 641-648 DOI: 10.1021/ar800241t.

Computed NMR spectra have been a major theme of the blog (see these posts). General consensus is that they can be enormously helpful in characterizing structures and stereochemistry, but there has been a nagging sense that one needs to use very large basis sets to get reasonable accuracies.

Bally and Rablen¹ now confront that claim and suggest instead that quite modest basis sets along with a number of flavors of DFT can provide very good ¹H NMR shifts. They examined 80 organic molecules spanning a variety of functional groups. A key feature is that these molecules exist as a single conformation or their conformational distribution is dominated by one conformer. This avoids the need of computing a large number of conformers and taking a Boltzman average of their shifts – a task that would likely require a much larger basis set than what they hope to get away with.

The most important conclusion: the WP04 functional,² developed by Cramer to predict proton spectra, with the very small 6-31G(d,p) basis set and incorporation of the solvent through PCM provides excellent cost/benefit performance. The rms error of the proton chemical shifts is 0.198 ppm, and this can be reduced to 0.140 ppm with scaling. The 6-31G(d) basis set is even better if one uses a linear scaling; its error is only 0.120 ppm. B3LYP/6-31G(d,p) has an rms only somewhat worse. Use of aug-cc-pVTZ basis sets, while substantially more time consuming, provides inferior predictions.

The authors contend that this sort of simple DFT computation, affordable for many organic systems on standard desktop PCs, should be routinely done, especially in preference to increment schemes that are components of some drawing programs. And if a synthesis group does not have the tools to do this sort of work, I’m sure there are many computational chemists that would be happy to collaborate!

References

(1) Jain, R.; Bally, T.; Rablen, P. R., "Calculating Accurate Proton Chemical Shifts of Organic Molecules with Density Functional Methods and Modest Basis Sets," J. Org. Chem. 2009, DOI: 10.1021/jo900482q.

(2) Wiitala, K. W.; Hoye, T. R.; Cramer, C. J., "Hybrid Density Functional Methods Empirically Optimized for the Computation of ¹³C and ¹H Chemical Shifts in Chloroform Solution," J. Chem. Theory Comput. 2006, 2, 1085-1092, DOI: 10.1021/ct6001016