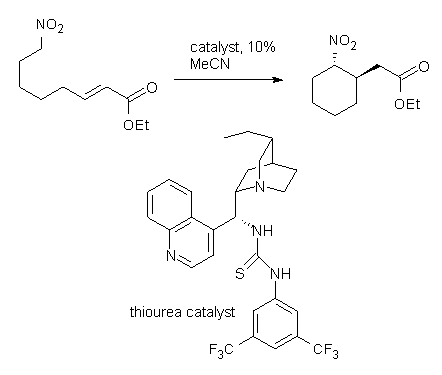
Coming on the heels of the very nice combined computational/experimental study of the enantioselective Strecker reaction by Jacobsen (see this post), there’s this JACS communication that really disappoints in its use of computational chemistry. Cobb uses yet another chiral thiourea to produce the enantioselective intramolecular Michael addition of nitronoates (Reaction1).1 The reaction goes with excellent diastereoselectivity and eneatioselectivity, and can even be done with a substrate to produce three chiral centers. This is very nice synthetic chemistry.
|
|
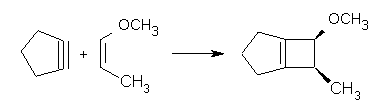
Reaction 1. dr >19:1 |
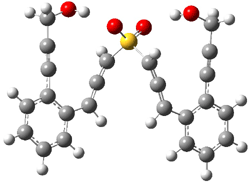
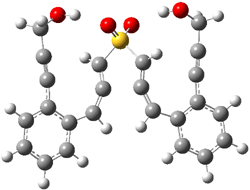
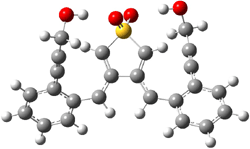
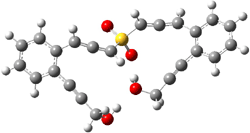
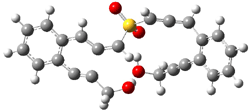
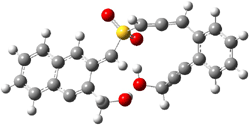
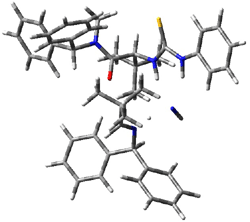
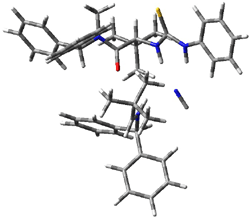
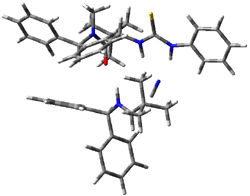
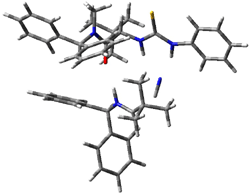
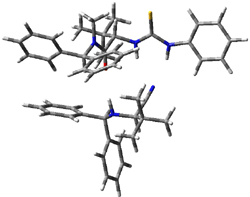
The lack of reactivity of the Z ester suggested that the thiourea must associate with both the nitro group and the ester carbonyl. The authors provide a B3LYP/3-21G complex of thiourea with a simple nitroester (once again without providing coordinates in the supporting materials!) to demonstrate this sort of association. But this single structure, at this very low computational level, with these simplified reagents, and lacking solvent (see Rzepa’s comment) really makes one wonder just what value this computation provides. It also goes to demonstrate just how much effort Jacobsen went through to provide substantive computational support for his proposed mechanism of action.
References
(1) Nodes, W. J.; Nutt, D. R.; Chippindale, A. M.; Cobb, A. J. A., "Enantioselective Intramolecular Michael Addition of Nitronates onto Conjugated Esters: Access to Cyclic γ-Amino Acids with up to Three Stereocenters," J. Am. Chem. Soc. 2009, 131, 16016-16017, DOI: 10.1021/ja9070915