The importance of the interactions between neighboring aromatic molecules cannot be overemphasized – π-π-stacking is invoked to explain the structure of DNA, the hydrophobic effect, molecular recognition, etc. Nonetheless, the nature of this interaction is not clear. In fact the commonly held notion of π-π orbital overlap is not seen in computations.

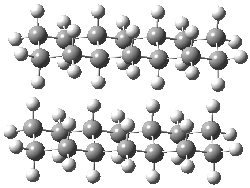
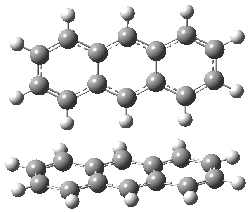
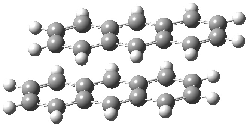
Grimme1 has now carefully examined the nature of aromatic stacking by comparison with aliphatic analogues. He has examined dimers formed of benzene 1, naphthalene 2, anthracene 3, and teracene 4 and compared these with the dimers of their saturated analogues (cyclohexane 1s, decalin 2s, tetradecahydroanthracene 3s, and octadecahydrotetracene 4s. The aromatic dimmers were optimized in the T-shaped and stacked arrangements, and these are shown for 3 along with the dimer of 3s in Figure 1. These structures are optimized at B97-D/TZV(2d,2p) – a functional designed for van der Waals compounds. Energies were then computed at B2LYP-D/QZV3P, double-hybrid functional that works very well for large systems.

Figure 1. Optimized structures of 3s, 3t, and 3a.

The energies for formation of the complexes are listed in Table 1. The first interesting result here is that the benzene and naphthalene dimmers (whether stacked or T-shaped) are bound by about the same amount as their saturated analogues. Grimme thus warns that “caution is required to not overestimate the effect of the π system”.

Table 1. Complexation energy (kcal mol-1)

 

1

2

3

4

T-shape (t)

2.82

5.46

8.25

11.12

Stacked saturated (s)

3.09

5.92

8.88

11.83

Stacked aromatics (a)

2.62

6.81

11.46

16.33

The two larger aromatics here do show a significantly enhanced complexation energy than their saturated analogues, and Grimme refers to this extra stabilization as the π-π stacking effect (PSE). Energy decomposition analysis suggests that electrostatic interactions actually favor the complexation of the saturated analogues over the aromatics. However, Pauli exchange repulsion essentially cancels the electrostatic attraction for all the systems, and it is dispersion that accounts for the dimerization energy. Dispersion increases with size of the molecule, and “classical” dispersion forces (the R-6 relationship) accounts for more than half of the dispersion energy in the saturated dimmers, while it is the non-classical, or orbital-based, dispersion that dominates in the stacked aromatic dimmers. Grimme attributes this to “special nonlocal electron correlations between the π electrons in the two fragments at small interplane distances”.

References

(1) Grimme, S., "Do Special Noncovalent π-π Stacking Interactions Really Exist?," Angew. Chem. Int. Ed., 2008, 47, 3430-3434, DOI: 10.1002/anie.200705157.

InChIs

1: InChI=1/C6H6/c1-2-4-6-5-3-1/h1-6H

1s: InChI=1/C6H12/c1-2-4-6-5-3-1/h1-6H2

2: InChI=1/C10H8/c1-2-6-10-8-4-3-7-9(10)5-1/h1-8H

2s: InChI=1/C10H18/c1-2-6-10-8-4-3-7-9(10)5-1/h9-10H,1-8H2

3: InChI=1/C14H10/c1-2-6-12-10-14-8-4-3-7-13(14)9-11(12)5-1/h1-10H

3s: InChI=1/C14H24/c1-2-6-12-10-14-8-4-3-7-13(14)9-11(12)5-1/h11-14H,1-10H2

4: InChI=1/C18H12/c1-2-6-14-10-18-12-16-8-4-3-7-15(16)11-17(18)9-13(14)5-1/h1-12H

4s: InChI=1/C18H30/c1-2-6-14-10-18-12-16-8-4-3-7-15(16)11-17(18)9-13(14)5-1/h13-18H,1-12H2