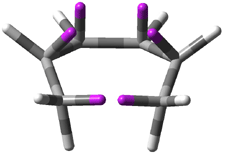
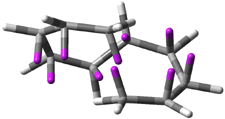
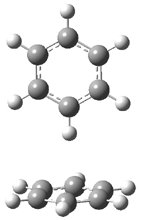
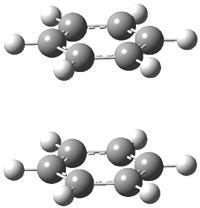
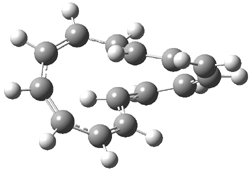
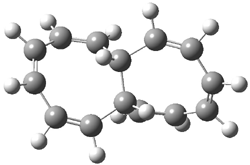
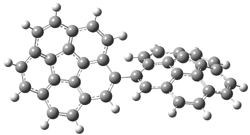
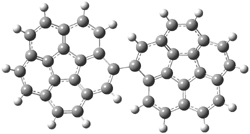
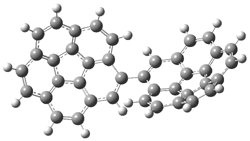
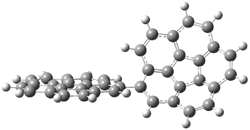
Careful consideration of orbital topolologies of pericyclic reactions has led to the recent flurry of activity related to Möbius aromaticity, homoaromaticity, and antiaromaticity. I discussed this briefly in Chapter 2 of the book and in these posts (1, 2, 3). Mauksh and Tsogoeva¹ have clearly demoted the four different topologies of the transition state of pericyclic reactions. One need to be concerned about (a) the topology of the molecule (does it will have the familiar twist of a Möbius strip or not?) and (b) the topology of the π-system (is there a phase inversion or not?). These four topologies are shown in Figure 1. The pink stick represents the positive lobe of the carbon p orbital.

(A)	(B)
(C)	(D)

Figure 1. Topologies of electrocyclization reactions.

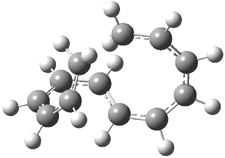
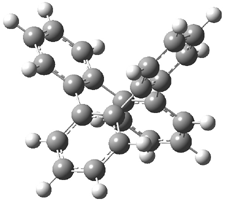
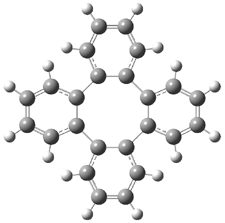
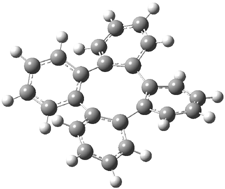
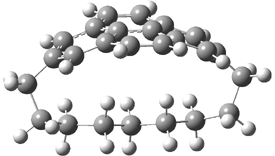
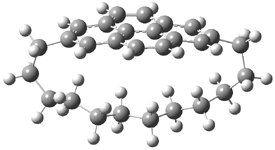
Three of these possibilities had been previously identified. The first (Fig. 1A) is the TS for the electrocyclization of 1,3,5-hexadiene. It has both Hückel topology of the molecule and the p orbitals. The second example (Fig. 1B) is the classic Zimmerman example of the electrocyclization of all-cis 1,3,5,7-octatetraene. It has Hückel topology of the molecule but one phase inversion of the p orbitals. The third example (Fig 1C) is the electrocyclization of (3E,5Z,7E)-1,3,5,7,9-decapentaene, proposed by Rzepa.² Here we have a Möbius topology but there is no phase inversion of the p orbitals.

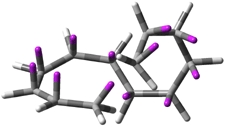
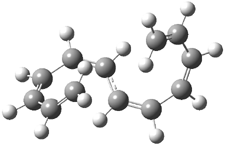
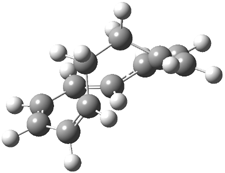
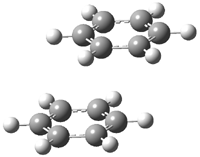
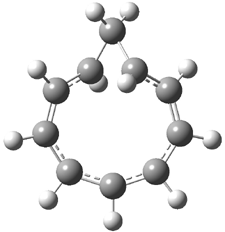
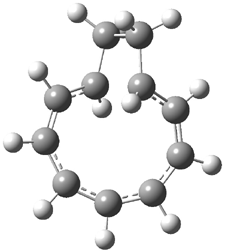
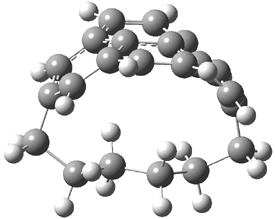
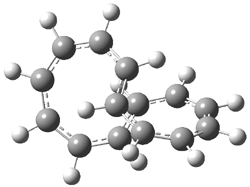
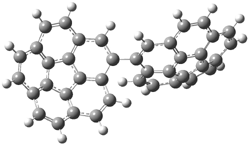
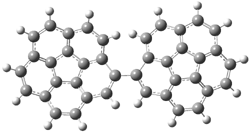
Mauksch and Tsogoeva report on the novel electrocylization of (3E,5E,7E,9E)-1,3,5,7,9,11-dodecahexaene (1), the fourth topology type (Fig 1d).¹ Here the molecule has the Möbius topology and there is one phase inversion. Figure 2 displays the geometries of the reactant 1, the electrocyclization transition state 2, and the product 3. The activation barrier is 35.7 kcal mol^-1. The NICS value at the center of the ring of the transition state is -12.8ppm , indicative of aromatic character, which is supported by the very small variation of the C-C distances (less than 0.02 Å).

1

2

3

Figure 2. B3LYP/6-31G* optimized geometries of 1-3.¹

Henry Rzepa has commented on this paper in his blog, along with detailing another example of this type of topology. In a second post, Henry discusses the issue of competition between aromatic and antiaromatic character in a related molecule.

References

(1) Mauksch, M.; Tsogoeva, S. B., "A Preferred Disrotatory 4n Electron Möbius Aromatic Transition State for a Thermal Electrocyclic Reaction," Angew. Chem. Int. Ed., 2009, 48, 2959-2963, DOI: 10.1002/anie.200806009

(2) Rzepa, H. S., "Double-twist Möbius aromaticity in a 4n+2 electron electrocyclic reaction," Chem. Commun., 2005, 5220-5222, DOI: 10.1039/b510508k.

InChIs

(3Z)-1,3,5-hexatriene: InChI=1/C6H8/c1-3-5-6-4-2/h3-6H,1-2H2/b6-5-
InChIKey=AFVDZBIIBXWASR-WAYWQWQTBR

(3Z,5Z)-octa-1,3,5,7-tetraene: InChI=1/C8H10/c1-3-5-7-8-6-4-2/h3-8H,1-2H2/b7-5-,8-6-
InChIKey=VXQUABLSXKFKLO-SFECMWDFBK

(3Z,5E,7Z)- 1,3,5,7,9-decapentaene: InChI=1/C10H12/c1-3-5-7-9-10-8-6-4-2/h3-10H,1-2H2/b7-5-,8-6-,10-9+
InChIKey=XKWRJEBRBGIQBA-LODOGNSSBI

(3Z,5Z,7Z,9Z)- 1,3,5,7,9,11-dodecahexaene (1): InChI=1/C12H14/c1-3-5-7-9-11-12-10-8-6-4-2/h3-12H,1-2H2/b7-5-,8-6-,11-9-,12-10-
InChIKey=GLCGEJFIZRSXBL-CAVFYFSLBM

(1Z,3Z,5E,7Z,9Z)-cyclododeca-1,3,5,7,9-pentaene (3): InChI=1/C12H14/c1-2-4-6-8-10-12-11-9-7-5-3-1/h1-10H,11-12H2/b2-1+,5-3-,6-4-,9-7-,10-8-
InChIKey=DULJMQFBRDFTQN-UWFJMCQMBK

Tetraphenylene 1 has a saddle-shape. The barrier for interconverting the two mirror image saddles has been estimated to range from about 5 kcal mol^-1 to as much as 220 kcal mol^-1. These estimates were made either experimentally, by placing a substituent on the ring and measuring the energy needed to racemize the compound or by fairly primitive computation (CNDO).

Bau, Wong and co-workers have prepared the dideutero and dimethyl derivations 2 and 3.¹ The optical activity of 2 turns out to be far too small to be useful (and the effort expended to determine if 2 is enantiopure is truly heroic). 3 proved to have significant optical activity and so could be used to determine if enantiopure 3 racemized under heating. Amazingly, there was no measurable loss of optical activity upon heating at 550 °C for 4 hours. Rather, heating at higher temperature lead to decomposition and no noticeable racemization. To corroborate this very high barrier for racemization, they optimized the structure of 1 in its ground state saddle geometry 1s and in its planar form 1p, presumably the transition state for racemization. These two geometries (B3LYP/6-31G(d,p) are shown in Figure 1. The barrier is an astounding 135.8 kcal mol^-1, consistent with the experiment.

They apparently did not perform a frequency computation to confirm that 1p is a true transition state. In fact, Müllen, Klärner, Roth and co-workers demonstrated that the transition state for the ring flip of 1 is not planar.² They located a C₁ TS using MM2 that is some 66 kcal mol^-1 above the tub-shaped ground state.

I have just published a follow up study on 1 and the related benzannulated cyclooctatetraenes.³ The true transition state for the ring flip of 1 has D₄ symmetry (1ts) and is shown in Figure 1. The barrier for ring flip through 1ts is 76.5 kcal mol^-1 at B3LYP/6-31G(d,p) (78.6 kcal mol^-1 at MP2/6-31G(d,p)). This barrier is too large to be overcome by heating, and so Bau and Wong are correct in concluding that decomposition proceeds racemization.

1	1p
1ts

Figure 1. B3LYP/6-31G(d,p) structures of 1,¹ 1p,¹ and 1ts.³

References

(1) Huang, H.; Stewart, T.; Gutmann, M.; Ohhara, T.; Niimura, N.; Li, Y.-X.; Wen, J.-F.; Bau, R.; Wong, H. N. C., “To Flip or Not To Flip? Assessing the Inversion Barrier of the Tetraphenylene Framework with Enantiopure 2,15-Dideuteriotetraphenylene and 2,7-Dimethyltetraphenylene,” J. Org. Chem. 2009, 74, 359-369, DOI: 10.1021/jo802061p.

(2) Müllen, K.; Heinz, W.; Klärner, F.-G.; Roth, W. R.; Kindermann, I.; Adamczk, O.; Wette, M.; Lex, J., “Inversionsbarrieren ortho,ortho’-verbücketer Biphenyle,” Chem. Ber. 1990, 123, 2349-2371.

(3) Bachrach, S. M., “Tetraphenylene Ring Flip Revisited,” J. Org. Chem. 2009, DOI: 10.1021/jo900413d.

InChIs

1: InChI=1/C24H16/c1-2-10-18-17(9-1)19-11-3-4-13-21(19)23-15-7-8-16-24(23)22-14-6-5-12-20(18)22/h1-16H/b19-17-,20-18-,23-21-,24-22-
InChIKey=KTQYWNARBMKMCX-LEYBOLSUBU

2: InChI=1/C24H16/c1-2-10-18-17(9-1)19-11-3-4-13-21(19)23-15-7-8-16-24(23)22-14-6-5-12-20(18)22/h1-16H/b19-17-,20-18-,23-21-,24-22-/i1D,3D
InChIKey=KTQYWNARBMKMCX-UEXWXQHBFR

3: InChI=1/C26H20/c1-17-11-13-23-24-14-12-18(2)16-26(24)22-10-6-4-8-20(22)19-7-3-5-9-21(19)25(23)15-17/h3-16H,1-2H3/b20-19-,24-23-,25-21-,26-22-
InChIKey=XIGXQJCZIXRTIQ-CURPJEMVBV

Liu has provided the link between pure the prototype organic aromatic compound (benzene) and the prototype pure inorganic aromatic (borazine).¹ His group has prepared 1,2-dihydro1,2-azaborine 1. Dixon has performed computations to support the identification of the molecule. For example, the computed and experimental chemical shifts are in nice agreement (see Table 1). The B3LYP/DZVP2 optimized structure of 1 is shown in Figure 1.

Table 1. Computed^a and experimental chemical shifts (ppm) of 1.¹

^aB3LYP/Alhrichs-vTZP.

Figure 1. B3LYP/DZVP2 optimized structure of 1.¹

The computations support the notion that 1 is truly aromatic. Its NICS(1) value is -7.27 ppm, close that of benzene (-10.39 ppm), and much more negative that that of borazine (-3.01 ppm). Reactions 1 and 2 compare the stability of 1 to benzene. These indicate that the resonance stabilization energy of 1 is about 13 kcal mol^-1 less than that of benzene, whose RSE is about 34 kcal mol^-1. Liu and Dixon thus consider 1 to be an aromatic compound and one that helps create a sort of organic, mixed organic-inorganic and inorganic aromatic continuum.

References

(1) Marwitz, A. J. V.; Matus, M. H.; Zakharov, L. N.; Dixon, D. D.; Liu, S.-Y., "A Hybrid Organic/Inorganic Benzene," Angew. Chem. Int. Ed. 2009, 48, 973-977, DOI: 10.1002/anie.200805554

InChIs

1: InChI=1/C4H6BN/c1-2-4-6-5-3-1/h1-6H
InChIKey=OGZZEGWWYQKMSO-UHFFFAOYAN

In sort of an afterword to a recent publication, Stanger¹ points out an error made by Hückel in arguing for stability of D_6h benzene over the hypothetical D_3h cyclohexatriene. Hückel constructed the first two matrices shown below to describe each molecule. The energy of benzene, predicted by this matrix, is 6α-8β, which is lower than that for cyclohexatriene, 6α-6β.

Stanger points out that implicit in Hückel’s argument is that the value of the H_ij element for the double bond is identical in value for the two compounds, (namely β), and the element is zero for the single bonds. Considering that the C-C double bond in cyclohexatriene should be shorter than that in benzene, Stanger suggests that its H_ij element should be larger than β and the H_ij element for the single bond should not be zero, but some small value reflecting the overlap between the p-orbitals. He suggests that the values for the single and double bond elements should be 0.4589β and 1.5050β, giving the bottom matrix below. This leads to an electronic energy of 6α-9.212β. In other words, this more appropriate model of cyclohexatriene has a lower π energy than does D_6h benzene! This is in accord with Shaik’s argument² that the π system of benzene acts to localize the bonds and it’s the σ system that is responsible for its delocalized structure.

Figure 1. Hückel matrices and eigenvalues for benzene (top),
traditional cyclohexatriene model (middle), and revised cyclohexatriene model (bottom).¹

References

(1) Stanger, A., "The Different Aromatic Characters of Some Localized Benzene Derivatives&#x2020," J. Phys. Chem. A, 2008, 112, 12849-12854, DOI: 10.1021/jp801634x

(2) Shaik, S.; Shurki, A.; Danovich, D.; Hiberty, P. C., "A different story of benzene," Journal of Molecular Structure: THEOCHEM, 1997, 398-399, 155-167, DOI: 10.1016/S0166-1280(96)04934-2.

Hobza¹ has published a very high-level computational study of the benzene dimer as a benchmark for this model of π-π stacking – a topic I have touched upon a number of times in this blog (post 1, post 2) . There are four local energy minima, shown in Figure 1. The most stable dimer is the tilted T-structure (TT), a structure often overlooked. Its complexation energy, computed at CCSD(T)/CBS, is 2.78 kcal mol^-1. Only slightly higher in energy is the parallel displaced structure (PD), with a stabilization energy of 2.70 kcal mol^-1. The T structure (T) is essentially isoenergetic with the PD one. The perfectly stacked structure (S) is much less stable, with a dimerization energy of 1.64 kcal mol^-1. The DTF-D method, using the BLYP functional with dispersion parameters optimized for the benzene dimer provide energies within 0.2 kcal mol^-1 of the computationally much more expensive benchmark values. As a word of caution though: use of more general dispersion parameters gives energies far worse and predicts the wrong energy order of the dimers.

TT 2.78 2.93 2.33	PD 2.70 2.88 2.57
T 2.69 2.80 2.03	S 1.64 1.84 1.45

Figure 1. Structures of the benzene dimer with stabilization energy (kcal mol^-1) computed at CCSD(T)/CBS (bold), DFT-D/BLYP with optimized parameters (italics), and DFT-D/BLYP with general parameters (plain).¹

References

(1) Pitonak, M.; Neogrady, P.; Rexac, J.; Jurecka, P.; Urban, M.; Hobza, P., "Benzene Dimer: High-Level Wave Function and Density Functional Theory Calculations," J. Chem. Theory Comput., 2008, 4, 1829-1834, DOI: 10.1021/ct800229h.

Rzepa has extended the concept of Möbius aromaticity to homoaromaticity.¹ 1 is the homoaromatic analogue of the tropylium cation. Topoligical electron density analysis, also known as Atoms-In-Molecules (AIM), indicates no bond path connecting C₁and C₇. However, the NICS value at the ring critical point of 1 is -11.5 ppm, indicative of aromaticity. 2 is the potential Möbius aromatic analogue of 1. Unlike 1 which has a plane of symmetry, 2 has a C₂ rotational axis of symmetry, as anticipated for a Möbius homoaromatic compound. However, there is no bond path connecting C₁ with C₉. But, the NICS value at the ring critical point of 2 is -11.3 ppm, supporting the notion of aromatic character! Suprisingly, the AIM analysis of the larger homologue 3 does have a bond path connecting C₁ to C₉, even though the distance separating these compounds is larger than in 2! Again the NICS value for 3 is negative (-9.8) and so it certainly appears to be Möbius homoaromatic.

The B3LYP/aug-cc-pVYZ structures of 1-3 are shown in Figure 1. As is Rzepa’s practice, he provides an extensive collection of data on the molecules he reports making great use of electronic depositories, and it looks like the ACS has now moved this “web-enhanced table” out into the open part of its web site: http://pubs.acs.org/doi/suppl/10.1021/ct8001915/suppl_file/index.html.

1	2
3

Figure 1. B3LYP/aug-cc-pVYZ optimized structures of 1-3.¹

References

(1) Allan, C. S. M.; Rzepa, H. S., "Chiral Aromaticities. A Topological Exploration of Möbius Homoaromaticity," J. Chem. Theory Comput., 2008, 4, 1841-1848, DOI: 10.1021/ct8001915

InChIs

1: InChI=1/C8H9/c1-2-4-6-8-7-5-3-1/h1-7H,8H2/q+1/b2-1-,5-3-,6-4-
InChIKey=ZINXKSGXPFSBNB-XCADPSHZBA

2: InChI=1/C10H11/c1-2-4-6-8-10-9-7-5-3-1/h1-9H,10H2/q+1/b2-1-,5-3-,6-4-,9-7-
InChIKey=HBJCUFQWAIKURE-BWYSQNKRBE

3: InChI=1/C11H13/c1-2-4-6-8-10-11-9-7-5-3-1/h1-9H,10-11H2/q+1/b2-1-,5-3-,6-4-,9-7-InChIKey=LUGAIBOLHSLVBJ-BWYSQNKRBF

The planar substituted cyclooctatetraene 1 has been prepared and characterized.¹ The B3LYP/6-31G(d) optimized geometry is shown in Figure 1.

1

Figure 1. B3LYP/6-31G(d) optimized geometry of 1.

The ¹H NMR spectrum of 1 shows the bridgehead proton has only a small upfield shift (Δδ = 0.18ppm) relative that of 2. This suggests that both molecules have similar degrees of aromaticity/antiaromaticity, and since both molecules display large bond alternation (ΔR = 0.169 Å in 1 and 0.089 Å in 2) one can argue that both paratropic and diatropic ring currents are attenuated in both molecules. However, the NICS value of 1 is 10.6 ppm, indicative of considerable antiaromatic character, though this NICS value is much reduced from that in planar cyclooctatetraene constrained to the ring geometry of 1 (22.1 ppm). Rabinowitz and Komatsu argue that large HOMO-LUMO gap of 1 is responsible for the reduced antiaromatic character of 1.

Though not discussed in their paper, the aromatic stabilization (destabilization) energy of 1 can be computed. I took two approaches, shown in Reactions 1 and 2. The energies of the two reactions are -13.8 kcal mol^-1 for Reaction 1 and -3.4 kcal mol^-1 for Reaction 2. The large exothermicity of Reaction 1 reflects the strain of packing the four bicyclo moieties near each other, forcing the neighboring bridgehead hydrogens to be directed right at each other. The strain is better compensated in Reaction 2 by using 3 as the reference. Since 3 is of C₂ symmetry, some strain relief remains a contributor to the overall reaction energy. Thus it appears that if 1 is antiaromatic, if manifests in little energetic consequence.

Reaction 1

Reaction 2

References

(1) Nishinaga, T.; Uto, T.; Inoue, R.; Matsuura, A.; Treitel, N.; Rabinovitz, M.; Komatsu, K., "Antiaromaticity and Reactivity of a Planar Cyclooctatetraene Fully Annelated with Bicyclo[2.1.1]hexane Units," Chem. Eur. J., 2008, 14, 2067-2074, DOI: 10.1002/chem.200701405

InChIs

1: InChI=1/C24H24/c1-9-2-10(1)18-17(9)19-11-3-13(4-11)21(19)23-15-7-16(8-15)24(23)22-14-5-12(6-14)20(18)22/h9-16H,1-8H2/b19-17-,20-18-,23-21-,24-22-
InChIKey=PUZMOHQGDBIGOO-LEYBOLSUBU

2: InChI=1/C18H18/c1-7-2-8(1)14-13(7)15-9-3-11(4-9)17(15)18-12-5-10(6-12)16(14)18/h7-12H,1-6H2
InChIKey=ULLLVKXTLZQQFF-UHFFFAOYAL

3: InChI=1/C14H16/c1-7-9-3-11(4-9)13(7)14-8(2)10-5-12(14)6-10/h9-12H,1-6H2/b14-13-
InChIKey=CSIHJUFBXMYVBH-YPKPFQOOBF

Once again into the breach – how much strain can an aromatic species withstand and remain aromatic? Cyranski, Bodwell and Schleyer employ the [n](2,7)pyrenophanes 1 to explore this question.¹ As the tethering bridge gets shorter, the pyrene framework must pucker, presumably reducing its aromatic character. Systematic shrinking allows one to examine the loss of aromaticity as defined by aromatic stabilization energy (ASE), magnetic susceptibility exaltation (Λ) and NICS, among other measures.

They examined the series of pyrenophanes where the tethering chain has 6 to 12 carbon atoms. I have shown the structures of three of these compounds in Figure 1. The bend angle α is defined as the angle made between the outside ring plane and the horizon. Relative ASE is computed using Reaction 1, which cleverly avoids the complication of exactly (a) what is the ASE of pyrene itself and (b) what is the strain energy in these compounds.

1a	1d
1g

Figure 1. B3LYP/6-311G** optimized geometries of 1a, 1d, and 1g.¹

Reaction 1

The results of the computations for this series of pyrenophanes is given in Table 1. The bending angle smoothly increases with decreasing length of the tether. The ASE decreases in the same manner. The ASE correlates quite well with the bending angle, as does the relative magnetic susceptibility exaltation. The NICS(1) values become less negative with decreasing tether length.

Table 1. Computed values for the pyrenophanes.

All of these trends are consistent with reduced aromaticity with increased out-of-plane distortion of the pyrene framework. What may be surprising is the relatively small loss of aromaticity in this sequence. Even though the bend angle is as large as almost 40°, the loss of ASE is only 16 kcal mol^-1, only about a quarter of the ASE of pyrene itself. Apparently, aromatic systems are fairly robust!

References

(1) Dobrowolski, M. A.; Cyranski, M. K.; Merner, B. L.; Bodwell, G. J.; Wu, J. I.; Schleyer, P. v. R.,
"Interplay of π-Electron Delocalization and Strain in [n](2,7)Pyrenophanes," J. Org. Chem., 2008, 73, 8001-8009, DOI: 10.1021/jo8014159

InChIs

1a: InChI=1/C22H20/c1-2-4-6-16-13-19-9-7-17-11-15(5-3-1)12-18-8-10-20(14-16)22(19)21(17)18/h7-14H,1-6H2
InChIKey=SJCYSWGQWCIONQ-UHFFFAOYAF

1b: InChI=1/C23H22/c1-2-4-6-16-12-18-8-10-20-14-17(7-5-3-1)15-21-11-9-19(13-16)22(18)23(20)21/h8-15H,1-7H2
InChIKey=VHVKAELFYUXZEM-UHFFFAOYAW

1c: InChI=1/C24H24/c1-2-4-6-8-18-15-21-11-9-19-13-17(7-5-3-1)14-20-10-12-22(16-18)24(21)23(19)20/h9-16H,1-8H2
InChIKey=HXPWDTNIUQNKLV-UHFFFAOYAQ

1d: InChI=1/C25H26/c1-2-4-6-8-18-14-20-10-12-22-16-19(9-7-5-3-1)17-23-13-11-21(15-18)24(20)25(22)23/h10-17H,1-9H2
InChIKey=DWYMZJZWMFVOIR-UHFFFAOYAM

1e: InChI=1/C26H28/c1-2-4-6-8-10-20-17-23-13-11-21-15-19(9-7-5-3-1)16-22-12-14-24(18-20)26(23)25(21)22/h11-18H,1-10H2
InChIKey=PZBADGOJPAEUIK-UHFFFAOYAZ

1f: InChI=1/C27H30/c1-2-4-6-8-10-20-16-22-12-14-24-18-21(11-9-7-5-3-1)19-25-15-13-23(17-20)26(22)27(24)25/h12-19H,1-11H2
InChIKey=YVZIXELCLJHDLW-UHFFFAOYAO

1g: InChI=1/C28H32/c1-2-4-6-8-10-12-22-19-25-15-13-23-17-21(11-9-7-5-3-1)18-24-14-16-26(20-22)28(25)27(23)24/h13-20H,1-12H2
InChIKey=QDAMLTATWKFTFB-UHFFFAOYAF

Pyrene: InChI=1/C16H10/c1-3-11-7-9-13-5-2-6-14-10-8-12(4-1)15(11)16(13)14/h1-10H
InChIKey=BBEAQIROQSPTKN-UHFFFAOYAB

4,9-dimethylenepyrene: InChI=1/C18H12/c1-11-9-13-5-4-8-16-12(2)10-14-6-3-7-15(11)17(14)18(13)16/h3-10H,1-2H2
InChIKey=XAAPFSHIUHWWCM-UHFFFAOYAM

Rzepa has published another study of Möbius aromaticity.¹ Here he examines the [14]annulene 1 using the topological method (AIM) and NICS. The B3LYP/6-31G(d) optimized structures of 1, the transition state 3 and product of the 8-e^– electroclization 2 are shown in Figure 1.

1 (0.0)

3 (4.56)

2 (0.07)

Figure 1. B3LYP/6-31G(d) optimized structures and relative energies (kcal mol^-1) of 1-3.¹

The topological analysis of 1 reveals a number of interesting features of the density. First, there are two bond critical points that connect the carbon atoms that cross over each other in the lemniscate structure 1 (these bond paths are drawn as the dashed lines in Scheme 1, connecting C₁ to C₈ and C₇ to C₁₄). These bond critical points have a much smaller electron density than for a typical C-C bond. With these added bond critical points come additional ring points, but not the anticipated 3 ring critical points. There is a ring critical point for the quasi-four member ring (C₁-C₁₄-C₇-C₈-C₁), but the expected ring point for each of the two 8-member ring bifurcate into two separate ring critical points sandwiching a cage critical point!

Scheme 1

Rzepa argues that the weak bonding interaction across the lemniscates is evidence for Möbius homoaromaticity in each half of 1. The NICS value at the central ring critical point is -18.6 ppm, reflective of overall Möbius aromaticity. But the NICS values at the 8-member ring ring critical points of -8.6 ppm and the cage critical points (-7.9 ppm) provide support for the Möbius homoaromaticity.

Transition state 3 corresponds to motion along the bond path of those weak bonds along either C₁-C₈ or C₇-C₁₄. This leads to forming the two fused eight-member rings of 2. An interesting thing to note is that there is only one transition state connecting 1 and 2 – even though one might think of the electrocyclization occurring in either the left or right ring. (Rzepa discusses this in a nice J. Chem. Ed. article.²) This transition state 3 is stabilized by Möbius aromaticity.

As an aside, Rzepa has once again made great use of the web in supplying a great deal of information through the web-enhanced object in the paper. As in the past, ACS continues to put this behind the subscriber firewall instead of considering it to be supporting material, which it most certainly is and should therefore be available to all.

References

(1) Allan, C. S. M.; Rzepa, H. S., "Chiral Aromaticities. AIM and ELF Critical Point and NICS Magnetic Analyses of Moöbius-Type Aromaticity and Homoaromaticity in Lemniscular Annulenes and Hexaphyrins," J. Org. Chem., 2008, 73, 6615-6622, DOI: 10.1021/jo801022b.

(2) Rzepa, H. S., "The Aromaticity of Pericyclic Reaction Transition States" J. Chem. Ed. 2007, 84, 1535-1540, http://www.jce.divched.org/Journal/Issues/2007/Sep/abs1535.html.

InChIs

1:
InChI=1/C14H14/c1-2-4-6-8-10-12-14-13-11-9-7-5-3-1/h1-14H/b2-1-,3-1-,4-2-,5-3-,6-4-,7-5+,8-6+,9-7-,10-8+,11-9-,12-10+,13-11-,14-12-,14-13-
InChIKey= RYQWRHUSMUEYST-YGYPEFQEBU

2: InChI=1/C14H14/c1-2-6-10-14-12-8-4-3-7-11-13(14)9-5-1/h1-14H/b2-1-,4-3-,9-5-,10-6-,11-7-,12-8-/t13-,14+
InChIKey= AMYHCQKNURYOBO-RFCQUTFOBS

Consider bicorannulenyl 1. Each corranulene unit is a bowl and each is chiral due to being monosubstituted. Additional chirality is due to the arrangement of the bowls along the C₁-C_1’ bond, the bond where the two rings join. So both rotation about the C₁-C_1’ bond and bowl inversion will change the local chirality (Scheme 1 distinguishes these two processes.) One might anticipate that the stereodynamics of 1 will be complicated!

Scheme 1

Rabinovitz, Scott, Shenhar and their groups have tackled the stereodynamics of 1.¹ (This is a very nice joint experimental and theoretical study and I wonder why it did not appear in JACS.) At room temperature and above, one observes a single set of signals, a singlet and eight doublets, in the ¹H NMR. Below 200 K, there are three sets of signals, evidently from three different diastereomers.

Each ring can have either P or M symmetry. The authors designate conformations using these symbols for each ring along with the value of the torsion angle about the C₁-C_1’ bond. So, for example, a PP isomer is the enantiomer of the MM conformer when their dihedral angles are of opposite sign.

DFT computations help make sense of these results. PBE0/6-31G* computations reveal all local minima and rotational and inversion transition states of 1. The lowest (free) energy structure is PP₄₄ (see Figure 1). A very small barrier separates it from PP₁₁₁; this barrier is related to loss of conjugation between the two rings. Further rotation must cross a much larger barrier (nearly 17 and 20 kcal mol^-1). These barriers result from the interaction of the C₂ hydrogen of one ring with either the C_2’ or C_10’ hydrogen, similar to the rotational barrier in 1,1’-binaphthyl. However, the barrier is lower in 1 than in 1,1’-binaphthyl due to the non-planar nature of 1 that allows the protons to be farther apart in the TS. Once over these large barriers, two local minima, PP_-45 and PP_-137, separated by a small barrier are again found.

PP44 0.0	PP-28 19.80	PP-45 3.38
PP111 1.54	PP166 16.76	PP-137 0.14

Figure 1. PBE0/6-31G* optimized geometries and relative free energies (kcal mol^-1) of the PP local minima (PP₄₄, PP₁₁₁, PP_-45, and PP_-137) and rotational transition states.¹

The lowest energy bowl inversion transition state (P₄₉) lies 9.6 kcal mole^-1 above PP₄₄. It is shown in Figure 2. The bowl inversion barrier is comparable to that found in other substituted corannulenes,² which are typically about 9-12 kcal mol^-1).

P49 9.58

Figure 2. PBE0/6-31G* optimized geometry and relative free energy of the lowest energy bowl inversion transition state.¹

Interestingly, it is easier to invert the bowl than to rotate about the C₁-C_1’ bond. And this offers an explanation for the experimental ¹H NMR behavior. At low temperature, crossing the low rotational barriers associated with loss of conjugation occurs. So, using the examples from Figure 1, PP₄₄ and PP₁₁₁ appear as a single time-averaged signal in the NMR. This leads to three pairs of enantiomers (S.PP/R.PP, S.MM/R.PP, and S.PM/R.MP), giving rise to the three sets of NMR signals.

References

(1) Eisenberg, D.; Filatov, A. S.; Jackson, E. A.; Rabinovitz, M.; Petrukhina, M. A.; Scott, L. T.; Shenhar, R., "Bicorannulenyl: Stereochemistry of a C40H18 Biaryl Composed of Two Chiral Bowls," J. Am. Chem. Soc. 2008, 73, 6073-6078, DOI: 10.1021/jo800359z.

(2) Wu, Y. T.; Siegel, J. S., "Aromatic Molecular-Bowl Hydrocarbons: Synthetic Derivatives, Their Structures, and Physical Properties," Chem. Rev. 2006, 106, 4843-4867, DOI: 10.1021/cr050554q.

InChIs

1: InChIKey = XZISQKATUXKXQW-UHFFFAOYAG