The chemical shift of the benzene proton is about 7.3ppm, significantly downfield from the range of olefinic protons (5.6-58.ppm). This is rationalized as the standard induced diatropic ring current, found in aromatic species. But what should we make of the chemical shift of the protons in cyclobutadiene at 5.8 ppm? Shouldn’t this be much further upfield?

Schleyer and Mo have applied the block localized wavefunction (BLW) technique to aromatic and antiaromatic chemical shifts.¹ In BLW, self-consistent localized orbitals are produced to describe a particular resonance structure. So, for benzene, BLW describes in effect 1,3,5-cyclohexatriene, lacking any resonance energy.  When chemical shifts are computed with the BLW description, the proton chemical shift is 6.6 ppm, and is even more upfield if the geometry is optimized (in D_3h symmetry) with the BLW method (δ=6.2ppm). Furthermore the NICS(0)_πzz (the tensor component corresponding to the perpendicular direction evaluated in the ring center using just the π orbitals) is -36.3 for benzene and 0.0 for the D_3h BLW variant, strongly indicating the role of cyclic delocalization in affecting chemical shifts.

Now for cyclobutadiene, the proton chemical shift of 5.7 ppm becomes 7.4 in the BLW case. NICS(0)_πzz for cyclobutadiene is +46.9 and +1.6 in the BLW case. The problem is that typical alkenes are poor references for cyclobutadiene – when resonance is turned off, the chemical shift does move downfield – indicating the expected upfield shift for cyclobutadiene. Schleyer and Mo suggest that 3,4-dimethylenecyclobutene is a more suitable reference; its ring protons have chemical shifts of 7.65ppm.

They also describe computations of benzocyclobutadiene and tricyclobutenabenzene and offer straightforward rationalizations of their aromatic vs. antiaromatic behavior.

References

(1) Steinmann, S. N.; Jana, D. F.; Wu, J. I.-C.; Schleyer, P. v. R.; Mo, Y.; Corminboeuf, C., "Direct Assessment of Electron Delocalization Using NMR Chemical Shifts," Angew. Chem. Int. Ed., 2009, 48, 9828-9833, DOI: 10.1002/anie.200905390

InChIs

benzene: InChI=1/C6H6/c1-2-4-6-5-3-1/h1-6H
InChIKey=UHOVQNZJYSORNB-UHFFFAOYAH

cyclobutadiene: InChI=1/C4H4/c1-2-4-3-1/h1-4H
InChIKey=HWEQKSVYKBUIIK-UHFFFAOYAI

3,4-dimethylenecyclobutene: InChI=1/C6H6/c1-5-3-4-6(5)2/h3-4H,1-2H2
InChIKey=WHCRVRGGFVUMOK-UHFFFAOYAP

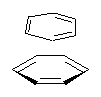
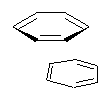
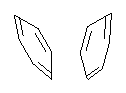
The nature of reactions of indolynes is the subject of two recent computational/experimental studies. There are three isomeric indolynes 1a-c which are analogues of the more famous benzyne (which I discuss in significant detail in Chapter 4.4 of my book).

One might anticipate that the indolynes undergo comparable reactions as benzyne, like Diels-Alder reactions and nucleophilic attack. In fact the indolynes do undergo these reactions, with unusual regiospecificity. For example, the reaction of the substituted 6,7-indolyne undergoes regioselective Diels-Alder cycloaddition with substituted furans (Scheme 1), but the reaction with the other indolynes gives no regioselection. ¹ Note that the preferred product is the more sterically congested adduct.

Scheme 1

In the case of nucleophilic addition, the nucleophiles add specifically to C₆ with substituted 6,7-indolynes (Scheme 2), while addition to 4,5-indolynes preferentially gives the C₅-adduct (greater than 3:1) while addition to the 5,6-indolynes preferentially gives the C₅-adduct), but with small selectivity (less than 3:1).²

Scheme 2

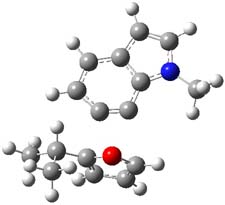
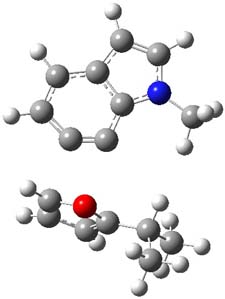
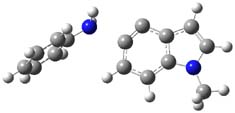
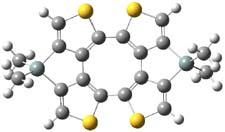
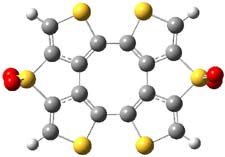
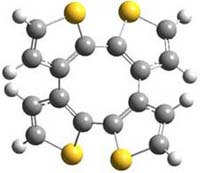
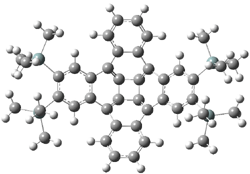
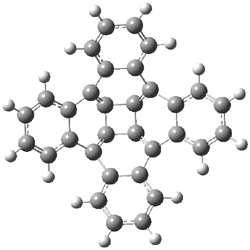
The authors of both papers – Chris Cramer studied the Diels-Alder chemistry and Ken Houk studied the nucleophilic reactions – employed DFT computations to examine the activation barriers leading to the two regioisomeric products. So for example, Figure 1 shows the two transition states for the reaction of 2c with 2-iso-propyl furan computed at MO6-2X/6-311+G(2df,p).

ΔG‡ = 9.7

ΔG‡ = 7.6

Figure 1. MO6-21/6-311+G(2df,p) optimized TSs for the reaction of 2-iso-propylfuran with 2c. Activation energy (kcal mol^-1) listed below each structure.¹

The computational results are completely consistent with the experiments. For the Diels-Alder reaction of 2-t-butylfuran with the three indolynes 2a-c, the lower computed TS always corresponds with the experimentally observed major product. The difference in the energy of the TSs leading to the two regioisomers for reaction with 2a and 2b is small (less than 1 kcal mol^-1), consistent with the small selectivity. On the other hand, no barrier could be found for the reaction of 2-t-butylfuran with 2c that leads to the major product. Similar results are also obtained for the nucleophilic addition – in all cases, the experimentally observed major product corresponds with the lower computed activation barrier.

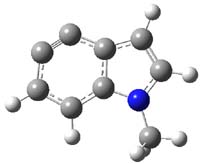
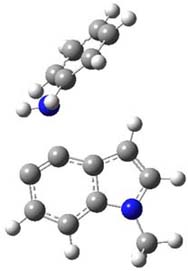
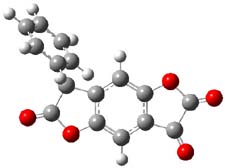
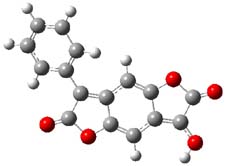
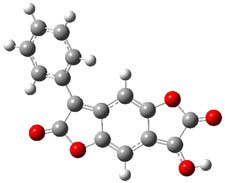
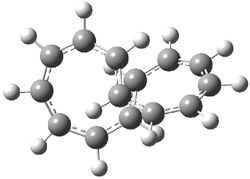
So what accounts for the regioselectivity? Both papers make the same argument, though couched in slightly different terms. Houk argues in terms of distortion energy – the energy needed to distort reactants to their geometries in the TS. As seen in Figure 2, the benzyne fragment of 2a is distorted, with the C-C-C angle at C₄ of 125° and at C₅ of 129°. In the transition states, the angle at the point of nucleophilic attack widens. Since the angle starts out wider at C₅, attack there is preferred, since less distortion is needed to achieve the geometry of the TS.

2a
TS at C4 ΔG‡ = 12.9	TS at C5 ΔG‡ = 9.9

Figure 2. B3LYP/6-31G(d) optimized structures of 2a and the TSs for the reaction of aniline with 2a. Activation energy in kcal mol^-1.²

Cramer argues in terms of the indolyne acting as an electrophile. Increasing substitution at the furan 2-position makes is better at stabilizing incipient positive charge that will build up there during a (very) asymmetric Diels-Alder transition state. This explains the increasing selectivity of the furan with increasing substitution. The indolyne acting as an electrophile means that the attack will lead from the center will lesser charge. In 2c, the C-C-C angle at C₆ is 135.3°, while that at C₇ is 117.2°. This makes C₇ more carbanionic and C₆ more carbocationic; therefore, the first bond made is to C₆, leading to the more sterically congested product. Note that Houk’s argument applies equally well, as C₆ is predistorted to the TS geometry.

References

(1) Garr, A. N.; Luo, D.; Brown, N.; Cramer, C. J.; Buszek, K. R.; VanderVelde, D., "Experimental and Theoretical Investigations into the Unusual Regioselectivity of 4,5-, 5,6-, and 6,7-Indole Aryne Cycloadditions," Org. Lett., 2010, 12, 96-99, DOI: 10.1021/ol902415s

(2) Cheong, P. H. Y.; Paton, R. S.; Bronner, S. M.; Im, G. Y. J.; Garg, N. K.; Houk, K. N., "Indolyne and Aryne Distortions and Nucleophilic Regioselectivites," J. Am. Chem. Soc., 2010, 132, 1267-1269, DOI: 10.1021/ja9098643

InChIs

1a: InChI=1/C8H5N/c1-2-4-8-7(3-1)5-6-9-8/h2,4-6,9H
InChIKey=RNDHGGYOIRREHC-UHFFFAOYAU

1b: InChI=1/C8H5N/c1-2-4-8-7(3-1)5-6-9-8/h3-6,9H
InChIKey=WWZQFJXNXMIWCD-UHFFFAOYAO

1c: InChI=1/C8H5N/c1-2-4-8-7(3-1)5-6-9-8/h1,3,5-6,9H
InChIKey=UHIRLIIPIXHWLT-UHFFFAOYAH

2a: InChI=1/C9H7N/c1-10-7-6-8-4-2-3-5-9(8)10/h3,5-7H,1H3
InChIKey=VTVUPAJGRVFCKI-UHFFFAOYAJ

2b: InChI=1/C9H7N/c1-10-7-6-8-4-2-3-5-9(8)10/h4-7H,1H3
InChIKey=KKPOWDDYMOXTFW-UHFFFAOYAN

2c: InChI=1/C9H7N/c1-10-7-6-8-4-2-3-5-9(8)10/h2,4,6-7H,1H3
InChIKey=MDAHOGWZOBLIEX-UHFFFAOYAZ

Here’s another attempt (almost successful!) in creating a planar cyclooctatetraene. Nishininaga and Iyoda have fused silicon and sulfur bridges to the COT framework, hoping to force the 8-member ring out of its preferred tub-shape into a planar structure.¹ They report the synthesis of 1, 2, and 3b along with their x-ray structures. They also calculated the structures at B3LYP/6-31G(d,p) for 1-4 , and these optimized structures are shown in Figure 1.

1 18° 19°	2 3.0° 4.3°
3a 7.0° (for 3b) 3.2° (for 3a)	4 39° 40°

Figure 1. B3LYP/6-31G(d,p) optimized geometries of 1-4. The experimental (top) and computed (Bottom in italics) value of α are listed for each compound.¹

The bent angle α is defined at the angle between the two planes that define the bottom of the tub and one of the sides. For COT itself, this angle is 40°, decidedly non-planar – as expected for a molecule avoiding the antiaromatic character it would have in its planar conformation. The computed and experimental values of α are shown in Figure 1. 4 is tub shaped. The value of α for 1 is about 18° – still tub shaped but flattened. But 2 and 3 are nearly planar, with experimental values of α about 3° and the computed values are similar.

So what is the character of the 8-member ring in these compounds. The computed NICS(0) values are 3.8 ppm for 4, the expected small value for a non-aromatic compound. (Note that the NICS value for COT is 2.9 ppm.) The values are much more positive for the other compounds: 12.7 ppm for 1, 17.4 ppm for 2, and 15.4 ppm for 3a. These compounds therefore display antiaromatic character yet they are isolable compounds!

References

(1) Ohmae, T.; Nishinaga, T.; Wu, M.; Iyoda, M., "Cyclic Tetrathiophenes Planarized by Silicon and Sulfur Bridges Bearing Antiaromatic Cyclooctatetraene Core: Syntheses, Structures, and Properties," J. Am. Chem. Soc., 2009, 132, 1066-1074, DOI: 10.1021/ja908161r

InChIs

1: InChI=1/C20H16S4Si2/c1-25(2)9-5-21-17-13(9)14-10(25)6-22-18(14)20-16-12(8-24-20)26(3,4)11-7-23-19(17)15(11)16/h5-8H,1-4H3/b19-17-,20-18-
InChIKey=DAVVQYAXJVCICC-CLFAGFIQBV

2: InChIKey=PBXVOLKKILUEGI-RFIZXXDFBX

3a: InChI=1/C16H4O4S6/c17-25(18)5-1-21-13-9(5)10-6(25)2-23-15(10)16-12-8(4-24-16)26(19,20)7-3-22-14(13)11(7)12/h1-4H/b14-13-,16-15-
InChIKey=VIDZCGPUBZEACC-RFIZXXDFBR

3b: InChI=1/C28H36O4S6Si4/c1-39(2,3)25-21-13-14-19(35-26(40(4,5)6)22(14)37(21,29)30)20-16-15-18(17(13)33-25)34-27(41(7,8)9)23(15)38(31,32)24(16)28(36-20)42(10,11)12/h1-12H3/b18-17-,20-19-
InChIKey=XXCFCYWSFICMIO-RXGVRZIVBS

4: InChI=1/C16H8S4/c1-5-17-13-9(1)10-2-6-18-14(10)16-12(4-8-20-16)11-3-7-19-15(11)13/h1-8H/b10-9-,12-11-,15-13-,16-14-
InChIKey=RSNUTSCZGMAXQJ-FNJUYVFOBD

The keto-enol tautomerization is an interesting system for probing relative energies of subtle effects, playing off different bond type (and their associated strengths) with conjugation and hydrogen bonding and strain. Lawrence and Hutchings have now extended this to include the interplay of aromaticity and antiaromaticity in the keto-enol tautomerization of benzodifurantrione 1.¹ The keto form 1k looks to be the favotable tautomer, containing an aromatic phenyl ring. The enol tautomer 1e requires the loss of that aromatic ring. Nonetheless, the enol structure is the only tautomer present in the crystal phase, and the enol tautomer is the dominant structure (if not the exclusive structure) in all solvents tested, including acetic acid, acetone, acetonitrile, chloroform, DMF, DMSO, propanol and toluene. The only solvents where the keto form is dominant are toluene and o-dichlorobenzene.

So, how does one rationalize this equilibrium? The B3LYP/6-311G(2d,p) structure of the two tautomers are shown in Figure 1. Note that there are two isomers of the enol form, differing on the orientation of the hydroxyl hydrogen. The syn isomer is the lowest energy form, in both the gas phase and in solution (PCM modeling acetonitrile, chlorobenzene and THF). So the enol form is the lowest energy structure when there are no special interactions involving hydrogen bonding or dipolar interactions with the solvent – there is an inherent energy preference for 1e.

1k
1e-anti	1e-syn

Figure 1. B3LYP/6-311G(2d,p) structures of the tautomers of 1.¹

To address that, they computed the NICS(0) values for each ring in the two tautomers. The pendant phenyl group is aromatic in both structures, as expected. The lactone ring has NICS values near 0 in both structures. The interior phenyl ring is aromatic (NICS = -7.5) in 1k but is non-aromatic in 1e, with NICS=-0.4. So the aromaticity of this ring is lost upon enolization, and thus would favor 1k. However, the terminal ring in the keto tautomer has NICS = +7.2, suggesting that it is antiaromatic, and upon enolization, the ring becomes slightly aromatic, with NICS = -2.1. Thus, the keto form is plagued by an antiaromatic ring, which is then lost in the enol form. The result is the interplay between losing an aromatic ring and its stabilization when the enol is formed balanced by also losing an antiaromatic ring with its destabilization. The authors do not offer any quantization (rightfully so!) of the stabilization/destabilization associated with these rings. But very subtle effects are clearly at play.

References

(1) Lawrence, A. J.; Hutchings, M. G.; Kennedy, A. R.; McDouall, J. J. W., "Benzodifurantrione: A Stable Phenylogous Enol," J. Org. Chem., 2010, 75, 690–701, DOI: 10.1021/jo9022155

InChIs

1k: InChI=1/C16H8O5/c17-14-10-7-11-9(6-12(10)21-16(14)19)13(15(18)20-11)8-4-2-1-3-5-8/h1-7,13H
InChIKey=GNWKSKHSRUSFBC-UHFFFAOYAC

1e: InChI=1/C16H8O5/c17-14-10-7-11-9(6-12(10)21-16(14)19)13(15(18)20-11)8-4-2-1-3-5-8/h1-7,17H
InChIKey=MZLQKOSFMRKQIO-UHFFFAOYAB

The recent synthesis and characterization of the quadrannulene 1 once again stretches
our notions of aromaticity.¹

The core of this system is a four-member ring with four fused-phenyl rings, forming the very small circulene (see this earlier post on circulenes). One might write other resonance structures for the molecule, which could include a central cyclobutadienyl fragment. However, the X-ray structure and computational analysis rejects any significant contribution of the cyclobutadienyl character. First, the four C-C bond of this central ring are 1.45 Å long, with an NBO bond order of 1.08, signifying single bonds. The bonds from the central 4-member ring are 1.36 Å long with bond order of 1.77 – these are double bonds. NICS computations attest to the central ring (+4.5 ppm) being more like [4]radialene (with a NICS value of -2.6 ppm) than like cyclobutadiene (with a NICS value of +16.5 ppm). The 6-member rings fused to the central ring have NICS values of -2.33 ppm, suggesting a non aromatic character, while the outer rings have NICS values of -10.7ppm, similar to that of benzene. The structure is clearly of radialene form. Nonetheless, the central ring possess extremely pyramidalized carbons, as seen in Figure 1, and their π-orbital axis vector, a measure of the pyramidalization, is 107°, which is similar to the idealized tetrahedral value of 109.47°. Despite this stain, the molecule is thermally stable to 170°C and reacts only slowly with air or base. This molecule will surely inspire further work in the small circulenes.

1

1a

Fig 1. B3LYP/6-311G** structures of 1 and its parent 1a (lacking the TMS groups).¹

References

(1) Bharat, R. B.; Bally, T.; Valente, A.; Cyranski, M. K.; Dobrzycki, L.; Spain, S. M.; Rempala, P.; Chin, M. R.; King, B. T., "Quadrannulene: A Nonclassical Fullerene Fragment," Angew. Chem. Int. Ed. 2009, DOI: 10.1002/anie.200905633

InChIs

1: InChI=1/C44H48Si4/c1-45(2,3)33-21-29-30(22-34(33)46(4,5)6)38-27-19-15-16-20-28(27)40-32-24-36(48(10,11)12)35(47(7,8)9)23-31(32)39-26-18-14-13-17-25(26)37(29)41-42(38)44(40)43(39)41/h13-24H,1-12H3
InChIKey=CDVRNAINHDQBCN-UHFFFAOYAM

1a: InChI=1/C32H16/c1-2-10-18-17(9-1)25-19-11-3-4-12-20(19)27-23-15-7-8-16-24(23)28-22-14-6-5-13-21(22)26(18)30-29(25)31(27)32(28)30/h1-16H
InChIKey=QTVPEOVCCYEZNL-UHFFFAOYAK

An emerging theme in this blog is Möbius systems, ones that can be aromatic or antiaromatic. Rzepa has led the way here, especially in examining annulenes with a twisted structure. Along with Schleyer and Schaefer, they have now explored a series of Möbius annulenes.¹ The particularly novel aspect of this new work is the examination of higher-order Möbius systems. In the commonly held notion of the Möbius strip, the strip contains a single half twist. Rzepa points out that the notion of twist must be considered as two parts, a part due to torsions and a part due to writhe.² We can think of the Möbius strip as formed by a ladder where the ends are connect such that the left bottom post connects with the top right post and the bottom right post connects with the top left post. Let’s now consider the circle created by joining the midpoints of each rug of the ladder. If this circle lies in a plane, then the torsion is π/N where N is the number of rungs in the ladder. But, the collection of midpoints does not have to lie in a plane, and if these points distort out of plane, that’s writhe and allows for less torsion in the strip.The sum of these two parts is called L_k and it will be an integral multiple of π. So the common Möbius strip has L_k = 1.

An example of a molecular analogue of the common Möbius strip is the annulene C₉H₉⁺ (1) – see figure 1. But Möbius strips can have more than one twist. Rzepa, Schleyer, and Schaefer have found examples with L_k = 2, 3, or 4. Examples are C₁₄H₁₄ (2) with one full twist (L_k = 2, two half twists), C₁₆H₁₆^2- (3) with three half twists, and C₂₀H₂₀²⁺ (4) with four half twists.

1	2
3	4

Figure 1. Structures of annulenes 1-4.

These annulenes with higher-order twisting, namely 2-4, are aromatic, as determined by a variety of measures. For example, all express negative NICS values, all have positive diagmagnetic exaltations, and all express positive isomerization stabilization energies (which are a measure of aromatic stabilization energy).

References

(1) Wannere, C. S.; Rzepa, H. S.; Rinderspacher, B. C.; Paul, A.; Allan, C. S. M.; Schaefer Iii, H. F.; Schleyer, P. v. R., "The Geometry and Electronic Topology of Higher-Order Charged M&oml;bius Annulenes" J. Phys. Chem. A 2009, ASAP, DOI: 10.1021/jp902176a

(2) Fowler, P. W.; Rzepa, H. S., "Aromaticity rules for cycles with arbitrary numbers of half-twists," Phys. Chem. Chem. Phys. 2006, 8, 1775-1777, DOI: 10.1039/b601655c.

Once more into the benzene dimer (see these previous posts: “Benzene dimer again“, “Benzene dimer“, “π-π stacking (part 2)“, “π-π stacking“)! Sherrill has published a detailed and impressive benchmark study of the benzene dimer in its three most important configurations: the D_6h stacked arrangement (1), the T-shaped arrangement (2) and the parallel displaced arrangement (3). ¹

First, they performed a careful extrapolation study to obtain accurate binding energies based on CCSD(T) with large basis sets. Then they compared the potential energy curves of the three configurations of benzene dimer obtained with this accurate method with those obtained with less computationally expensive methods. These alternates include RI-MP2, SCS-MP2 and a variety of different density functional. Their results are summarized in Table 1. The upshot is that the SCS-MP2 results are very similar to the much more expensive CCDS(T) values. And while the errors are a bit larger with the DFT methods, their performance is really quite good, especially given their dramatically lower costs. (Note that the “-D” indicates inclusion of Grimme’s dispersion correction term.) Particularly worth mentioning is the very fine performance of the MO6-2X functional.

Table 1. Binding energies (kcal mol^-1) of the three benzene dimers with different computational methods.

References

(1) Sherrill, C. D.; Takatani, T.; Hohenstein, E. G., "An Assessment of Theoretical Methods for Nonbonded Interactions: Comparison to Complete Basis Set Limit Coupled-Cluster Potential Energy Curves for the Benzene Dimer, the Methane Dimer, Benzene-Methane, and Benzene-H₂S" J. Phys. Chem. A 2009, ASAP, DOI: 10.1021/jp9034375

The octaphyrin 1 has been prepared and its crystal structure and electronic circular dichroism (ECD) spectra reported.¹ The x-ray structure identified the compound as having the M,M helical structure. The optical rotation however could not be determined.

Rzepa now reports the computed ECD spectrum and optical activity of 1 and some related compounds.² These computed spectra were obtained using TD0DFT with the B3LYP/6-31G(d) method with the CPCM treatment of the dichloromethane solvent. (The structure of 1 and other computed properties are available from the enhanced web table that Rzepa has deposited with the article (here). Once again this material seems to be available only to subscribers! My repeated discussions with ACS Pubs people that these “web objects” should be treated as data and not as copyrighted materials have fallen on deaf ears.) The computed ECD spectrum matches nicely with the experimental one, except that the signs at 570 and 620 nm are opposite. Rzepa suggests that either the compound is really of P,P configuration or the authors of experimental work have erroneously switched their assignments.

The computed value of [α]_D of 1 is about -4000 °, with the negative sign in agreement with the sign for [α]_D of M-hexahelicene. However, what is truly fantastic is the magnitude of the optical activity of the dication of 1 produced by loss of 2 electrons. This dication should be aromatic and it is predicted to have [α]₁₀₀₀ = -31597°!

References

(1) Werner, A.; Michels, M.; Zander, L.; Lex, J.; Vogel, E., ""Figure Eight" Cyclooctapyrroles: Enantiomeric Separation and Determination of the Absolute Configuration of a Binuclear Metal Complex," Angew. Chem. Int. Ed. 1999, 38, 3650-3653, DOI: 10.1002/(SICI)1521-3773(19991216)38:24<3650::AID-ANIE3650>3.0.CO;2-F

(2) Rzepa, H. S., "The Chiro-optical Properties of a Lemniscular Octaphyrin," Org. Lett. 2009, 11, 3088–3091DOI: 10.1021/ol901172g

The Kim and Osuka groups have reported another Möbius aromatic porphyrin, 1, a 28 π-electron system.¹ This hexaporphyrin is produced without the need for low temperature, complexation with a metal or protonation (see this post for a discussion of their earlier work). The x-ray crystal structure shows the Möbius twist, and the ¹H NMR shifts of the interior protons at 2.22 and 1.03 ppm. B3LYP/6-31G** computations indicate a NICS value at the center of the molecule of -11.8 ppm. These are consistent with aromatic behavior.

References

(1) Tokuji, S.; Shin, J.-Y.; Kim, K. S.; Lim, J. M.; Youfu, K.; Saito, S.; Kim, D.; Osuka, A., "Facile Formation of a Benzopyrane-Fused [28]Hexaphyrin That Exhibits Distinct Möbius Aromaticity," J. Am. Chem. Soc. 2009, 131, 7240-7241, DOI: 10.1021/ja902836x.

InChIs

1: InChIKey=YGJLOPZWRVMFIJ-XFAHNSIYBC

Yet more on the benzene dimer. Lesczynski has optimized 9 different benzene dimer configurations, shown in Scheme 1.¹ There are two T-shaped isomers, where a hydrogen from one benzene interacts with the center of the π-cloud of the second. There are two bent versions of the T-shape, called Bent-T-shape. There are two sandwich configurations and two variants where the benzenes are parallel but displaced. Lastly, they report on a new variant, the V-shape configuration. (Once again, the author has not deposited the structures and so I can’t produce interactive figures!)

Scheme 1

The structures were optimized at MP2/aug-cc-pVDZ and then single point energies computed at MP4(SDTQ)/aug-cc-pVDZ and corrected for basis set superposition error. I list these energies in Table 1. They authors note that in comparison with CCSD(T) computations one has to adjust the amount of BSSE correction – which just supports my long-held contention that the standard counterpoise correction overcompensates and that we really have no reliable way of correcting for BSSE.

Table 1. Dimerization energies (kcal mol^-1) at MP4(SDTQ)/aug-cc-pVDZ.¹

The relative energies of the 9 configurations are similar, indicating a very flat potential energy surface. The lowest energy structure is BT-2, and the V-shape configuration is the least favorable of the nine geometries examined.

References

(1) Dinadayalane, T. C.; Leszczynski, J., "Geometries and stabilities of various configurations of benzene dimer: details of novel V-shaped structure revealed " Struct. Chem. 2009, 20, 11-20, DOI: 10.1007/s11224-009-9411-6.