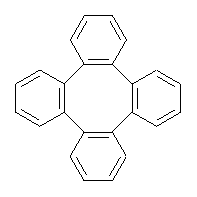
Tetraphenylene 1 has a saddle-shape. The barrier for interconverting the two mirror image saddles has been estimated to range from about 5 kcal mol-1 to as much as 220 kcal mol-1. These estimates were made either experimentally, by placing a substituent on the ring and measuring the energy needed to racemize the compound or by fairly primitive computation (CNDO).
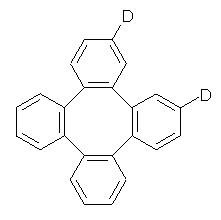
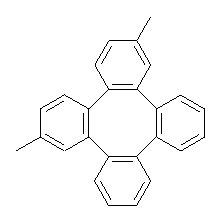
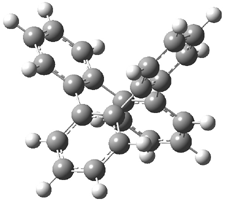
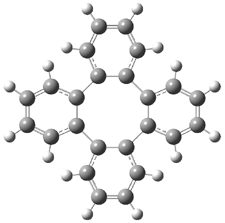
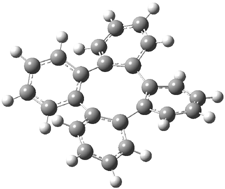
Bau, Wong and co-workers have prepared the dideutero and dimethyl derivations 2 and 3.1 The optical activity of 2 turns out to be far too small to be useful (and the effort expended to determine if 2 is enantiopure is truly heroic). 3 proved to have significant optical activity and so could be used to determine if enantiopure 3 racemized under heating. Amazingly, there was no measurable loss of optical activity upon heating at 550 °C for 4 hours. Rather, heating at higher temperature lead to decomposition and no noticeable racemization. To corroborate this very high barrier for racemization, they optimized the structure of 1 in its ground state saddle geometry 1s and in its planar form 1p, presumably the transition state for racemization. These two geometries (B3LYP/6-31G(d,p) are shown in Figure 1. The barrier is an astounding 135.8 kcal mol-1, consistent with the experiment.
|
|
|
|
|
|
They apparently did not perform a frequency computation to confirm that 1p is a true transition state. In fact, Müllen, Klärner, Roth and co-workers demonstrated that the transition state for the ring flip of 1 is not planar.2 They located a C1 TS using MM2 that is some 66 kcal mol-1 above the tub-shaped ground state.
I have just published a follow up study on 1 and the related benzannulated cyclooctatetraenes.3 The true transition state for the ring flip of 1 has D4 symmetry (1ts) and is shown in Figure 1. The barrier for ring flip through 1ts is 76.5 kcal mol-1 at B3LYP/6-31G(d,p) (78.6 kcal mol-1 at MP2/6-31G(d,p)). This barrier is too large to be overcome by heating, and so Bau and Wong are correct in concluding that decomposition proceeds racemization.
|
1 |
1p |
|
1ts |
|
Figure 1. B3LYP/6-31G(d,p) structures of 1,1 1p,1 and 1ts.3
References
(1) Huang, H.; Stewart, T.; Gutmann, M.; Ohhara, T.; Niimura, N.; Li, Y.-X.; Wen, J.-F.; Bau, R.; Wong, H. N. C., “To Flip or Not To Flip? Assessing the Inversion Barrier of the Tetraphenylene Framework with Enantiopure 2,15-Dideuteriotetraphenylene and 2,7-Dimethyltetraphenylene,” J. Org. Chem. 2009, 74, 359-369, DOI: 10.1021/jo802061p.
(2) Müllen, K.; Heinz, W.; Klärner, F.-G.; Roth, W. R.; Kindermann, I.; Adamczk, O.; Wette, M.; Lex, J., “Inversionsbarrieren ortho,ortho’-verbücketer Biphenyle,” Chem. Ber. 1990, 123, 2349-2371.
(3) Bachrach, S. M., “Tetraphenylene Ring Flip Revisited,” J. Org. Chem. 2009, DOI: 10.1021/jo900413d.
InChIs
1: InChI=1/C24H16/c1-2-10-18-17(9-1)19-11-3-4-13-21(19)23-15-7-8-16-24(23)22-14-6-5-12-20(18)22/h1-16H/b19-17-,20-18-,23-21-,24-22-
InChIKey=KTQYWNARBMKMCX-LEYBOLSUBU
2: InChI=1/C24H16/c1-2-10-18-17(9-1)19-11-3-4-13-21(19)23-15-7-8-16-24(23)22-14-6-5-12-20(18)22/h1-16H/b19-17-,20-18-,23-21-,24-22-/i1D,3D
InChIKey=KTQYWNARBMKMCX-UEXWXQHBFR
3: InChI=1/C26H20/c1-17-11-13-23-24-14-12-18(2)16-26(24)22-10-6-4-8-20(22)19-7-3-5-9-21(19)25(23)15-17/h3-16H,1-2H3/b20-19-,24-23-,25-21-,26-22-
InChIKey=XIGXQJCZIXRTIQ-CURPJEMVBV

Henry Rzepa responded on 09 Apr 2009 at 2:05 am #
What a fascinating problem. Might I ask some questions about it?
1. The equilibrium state of 1 has D2d symmetry, that is to say it has planes of symmetry which mean it is not chiral.
2. 2 or 3 have lower symmetry, C2, which of course makes them both chiral.
2. The transition state for enantiomerization of 1 (1ts) has D4 symmetry. This has no planes of symmetry and is now chiral, unlike the equilibrium state. The transition states for 2 or 3 presumably have C2 symmetry.
Normally, one finds that transition states for interconversion of one enantiomer to another involve passage through a transition state with at least one plane of symmetry (the very famous proof by Meerwein of the formation of a carbocation intermediate for solvolysis of isobornyl chloride, for which the transition state has a plane of symmetry).
It is of course possible to pass from one enantiomer to the opposite enantiomer via a reaction path along which all the intermediates are also chiral (the so called principle of chiral connectednes; see P. W. Fowler,
Symmetry Culture and Science, 2005, 16, 321–334). Given the chiral nature of 1ts, is that the case here? In which case it would be a relatively rare example of such chiral connectedness, and is worth noting! Or is there somewhere a transition state with a plane of symmetry?
Henry Rzepa responded on 11 Apr 2009 at 2:04 am #
A follow up to my above comments.
The transition state for inversion of tetraphenylene that Steve refers to (1ts) has an imaginary mode of B2 symmetry with a wavenumber of 46i cm-1. An IRC following this mode in either direction does appear to lead to the two tub conformations (which when substituted with eg methyl groups are enantiomers). So for the (optically active methyl isomer), this on the face of it does appear to be an example of chiral connectedness in which both equilibrium and transition state are connected by a continuously chiral pathway. It would be interesting to identify other simple examples!
Steve: a plea! Can you include in your blog a Jmol model animating e.g. the B2 mode? It certainly is an unusual mode, and well worth a look. The nature of WordPress means that people commenting on your posts cannot themselves include either pictures or indeed Jmol models.
The magnitude of the imaginary mode is also interesting, being unusually low for such a relatively small molecule involving a process with such a high barrier. One might suppose that part of the reason is that the mode is heavily delocalized over the entire molecule (most transition modes are in fact relatively localized, which means the reduced mass of the mode is relatively low). But still, it does mean the potential near the transition state is very flat, and one has to wonder why? We once observed a similar phenomenon for the enantiomerization of Co(acac)3, which has a similar propellor shape (in the equilibrium state), and a similar barrier (around 60 kcal/mol), but for which the transition mode also had a very small wavenumber. On e has to wonder whether such low energy modes for such high barrier reactions have a more fundamental reason for their behaviour. I did speculate that 1ts might have some Mobius character mixing in, but the selection rule is not correct to explain the above observation.
Finally I would like to note a much neglected molecule, first reported as 10.1002/anie.198801851 quite a few years back, which is the tetra homo derivative of molecule 1, and a stable crystalline antiaromatic [24] annulene to boot. It is one of my favourite annulenes! Amongst other properties, it might well be an example of a homoClar system, where the antiaromaticity is attenuated by forming four homoaromatic Clar islands. Such Clar islands are common in stable antiaromatic molecules (yes, an apparently oxymoronic statement!).
sbachrach responded on 11 Apr 2009 at 9:46 am #
Henry,
Your reply to your own comment beat me to the punch regarding the nature of the imaginary frequency. I had done an IRC calculation as you suggest and it does appear to properly connect the two tub-shape ground states. I wish I hadn’t been so focused on the barrier height while doing the write-up and I might have caught the interesting topology of the inversion that you brought out here!
I am happy to post the imaginary mode in Jmol, but I must confess to not knowing how to do this. (Jmol is not my primary visualization tool.) So if someone lets me know how I incorporate the vibrational mode information into Jmol, I’m happy to post it. I do have the Gaussian output file.
Henry Rzepa responded on 11 Apr 2009 at 2:38 pm #
Steve: A question about the aromaticity of the rings in 1ts. The four benzo groups might be expected to be aromatic, and have e.g. a NICS(0) corresponding to a diatropic value, whilst the central ring would be the opposite (paratropic). The interesting question is whether either attenuates the other, and how the values compare to the equilibrium state. Did you calculate these perchance?
sbachrach responded on 14 Apr 2009 at 1:11 pm #
I have computed the NICS(0) values for the 8-member ring and the 6-member rings the three critical points of 1. These are listed in the table below:
So, the ground state has four regular phenyl rings and the central 8-member ring is non-aromatic, consistent with its tub-shape and strong bond alternation. The planar structure has an anti-aromatic 8-member ring, with weaker aroamicity in the phenyl rings than in the ground state structure. The true transition state (1ts) is similar to the planar structure, but with a somewhat lesser anti-aromatic central ring and slightly more aromatic phenyl groups. Yet another reason why the planar structure is avoided.
Henry Rzepa responded on 15 Apr 2009 at 12:27 pm #
One remaining unsolved mystery is why the imaginary mode is so small. I have noticed such small modes (40 – 60 cm-1) in other contexts, particularly when the mode is spread evenly throughout a very heavy system. Jimmy Stewart has recently published a theory of why transition modes have a tendency to “localize”. As more and more TS are calculated for very large molecules such as for enzyme mechanisms, no doubt a taxonomy of diffuse and localized TS modes vs the barrier to reaction they represent will start to emerge.
The NICS noted in the previous comment suggests that 1ts is nothing particularly special in its electronic properties, ie the low value of the TS mode is not due to special local effects.
Henry Rzepa responded on 20 Apr 2009 at 12:14 pm #
I noted earlier the paucity of examples of mechanisms for enantiomerization where the entire pathway is chirally connected. Patrick Fowler has alerted me to two articles by Paul Schleyer which address this point via two fascinating examples. They are at 3.0.CO;2-I”>10.1002/1521-3773(20000804)39:15<2756::AID-ANIE2756>3.0.CO;2-I and 0.1002/anie.199718561. They also detail much of the background behind this topic.