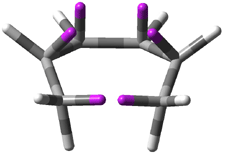
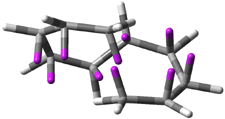
Careful consideration of orbital topolologies of pericyclic reactions has led to the recent flurry of activity related to Möbius aromaticity, homoaromaticity, and antiaromaticity. I discussed this briefly in Chapter 2 of the book and in these posts (1, 2, 3). Mauksh and Tsogoeva1 have clearly demoted the four different topologies of the transition state of pericyclic reactions. One need to be concerned about (a) the topology of the molecule (does it will have the familiar twist of a Möbius strip or not?) and (b) the topology of the π-system (is there a phase inversion or not?). These four topologies are shown in Figure 1. The pink stick represents the positive lobe of the carbon p orbital.
|
(A) |
(B) |
|
(C) |
(D) |
Figure 1. Topologies of electrocyclization reactions.
Three of these possibilities had been previously identified. The first (Fig. 1A) is the TS for the electrocyclization of 1,3,5-hexadiene. It has both Hückel topology of the molecule and the p orbitals. The second example (Fig. 1B) is the classic Zimmerman example of the electrocyclization of all-cis 1,3,5,7-octatetraene. It has Hückel topology of the molecule but one phase inversion of the p orbitals. The third example (Fig 1C) is the electrocyclization of (3E,5Z,7E)-1,3,5,7,9-decapentaene, proposed by Rzepa.2 Here we have a Möbius topology but there is no phase inversion of the p orbitals.
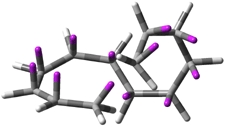
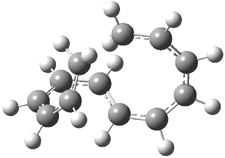
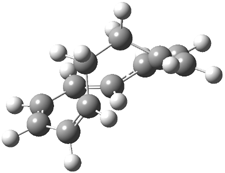
Mauksch and Tsogoeva report on the novel electrocylization of (3E,5E,7E,9E)-1,3,5,7,9,11-dodecahexaene (1), the fourth topology type (Fig 1d).1 Here the molecule has the Möbius topology and there is one phase inversion. Figure 2 displays the geometries of the reactant 1, the electrocyclization transition state 2, and the product 3. The activation barrier is 35.7 kcal mol-1. The NICS value at the center of the ring of the transition state is -12.8ppm , indicative of aromatic character, which is supported by the very small variation of the C-C distances (less than 0.02 Å).
|
1 |
|
2 |
|
3 |
Figure 2. B3LYP/6-31G* optimized geometries of 1-3.1
Henry Rzepa has commented on this paper in his blog, along with detailing another example of this type of topology. In a second post, Henry discusses the issue of competition between aromatic and antiaromatic character in a related molecule.
References
(1) Mauksch, M.; Tsogoeva, S. B., "A Preferred Disrotatory 4n Electron Möbius Aromatic Transition State for a Thermal Electrocyclic Reaction," Angew. Chem. Int. Ed., 2009, 48, 2959-2963, DOI: 10.1002/anie.200806009
(2) Rzepa, H. S., "Double-twist Möbius aromaticity in a 4n+2 electron electrocyclic reaction," Chem. Commun., 2005, 5220-5222, DOI: 10.1039/b510508k.
InChIs
(3Z)-1,3,5-hexatriene: InChI=1/C6H8/c1-3-5-6-4-2/h3-6H,1-2H2/b6-5-
InChIKey=AFVDZBIIBXWASR-WAYWQWQTBR
(3Z,5Z)-octa-1,3,5,7-tetraene: InChI=1/C8H10/c1-3-5-7-8-6-4-2/h3-8H,1-2H2/b7-5-,8-6-
InChIKey=VXQUABLSXKFKLO-SFECMWDFBK
(3Z,5E,7Z)- 1,3,5,7,9-decapentaene: InChI=1/C10H12/c1-3-5-7-9-10-8-6-4-2/h3-10H,1-2H2/b7-5-,8-6-,10-9+
InChIKey=XKWRJEBRBGIQBA-LODOGNSSBI
(3Z,5Z,7Z,9Z)- 1,3,5,7,9,11-dodecahexaene (1): InChI=1/C12H14/c1-3-5-7-9-11-12-10-8-6-4-2/h3-12H,1-2H2/b7-5-,8-6-,11-9-,12-10-
InChIKey=GLCGEJFIZRSXBL-CAVFYFSLBM
(1Z,3Z,5E,7Z,9Z)-cyclododeca-1,3,5,7,9-pentaene (3): InChI=1/C12H14/c1-2-4-6-8-10-12-11-9-7-5-3-1/h1-10H,11-12H2/b2-1+,5-3-,6-4-,9-7-,10-8-
InChIKey=DULJMQFBRDFTQN-UWFJMCQMBK


Henry Rzepa responded on 29 Apr 2009 at 12:14 pm #
Steve describes the topological possibilities, correcting identifying that it is the phase shift that characterizes them, not the ambiguous stereochemical term disrotatory or conrotatory. But there is another term into which some confusion has crept. In the example attributed to myself, he notes there is no phase inversion, but nevertheless the system is still described by myself as Möbius. How can that be? The terminology for systems with no phase inversion is historically called Huckel, not Möbius.
My basis for calling a system which has no phase inversions Möbius goes back to August himself. His actual representation of the famous band is rather different from that normally presented; it is flat packed, and we can see it everywhere as the recycling logo (I would include a graphic of this, but WordPress does not allow these in comments). But alongside this, Möbius in fact identified an entire family of strips, the higher order ones having two, three, and more half twists (all in flat packed form!). They al have one attribute in common; they are all chiral! The untwisted band (mapping to e.g. benzene) is the only achiral example. Now to the terminology. The system attributed to me was a doubly twisted example. This corresponds to the second of the examples Möbius gives. In this family, those with an odd number of twists will have a phase inversion in a 2p AO basis, those with an even (but non zero) number of twists will have no phase inversion. I argue they are all Möbius, and this is because they are all chiral. I prefer to keep the specific term Hückel reserved for the only member of this series which is achiral. Furthermore, all members of the Möbius series can have associated aromaticity, and it seems useful to coin the term chiral aromaticity. Clearly again, Hückel is different in being achiral. These arguments, at least in part, can be found at 10.1021/ja710438j if you want further details.
I might add that one can go further, and classify the π-electron densities arising from these topologies in terms of Torus knots (for the ones deriving from an odd number of twists) and Torus links (for those with even twists). Here too, benzene can be considered the outlier, since its a link which is not actually linked.
So, who deserves the term for twisted systems with no phase inversion? Hückel, who only ever considered the special case of benzene, or Möbius, who clearly saw that his famous band was in fact a whole family of bands? I think I have made my preference clear, but it is the community that will decide!
Henry Rzepa responded on 29 Apr 2009 at 1:15 pm #
Apologies, I always manage to think of one more thing after pressing the submit button. Johann Listing also deserves a mention! In 1847, he published a seminal work on Topology (see here for images of some of the pages of this article), as translated and interpreted by Peter Guthrie Tait, he clearly describes what happens when a band with three twists is cut down the middle (the resulting trefoil knot is clearly shown in two enantiomeric representations), and notes in passing that the band with just one half twist is a well known Juggler’s trick! Listing seems to have overlooked the double twisted band (but in the dense German the article is written it, it may well be mentioned somewhere). Möbius is normally credited with 1858 as the year of his own discovery, ie 11 years later than the article above. Arguably the term Möbius should everywhere be replaced by Listing-Möbius.
I might also mention that Listing was a pupil of Gauss (of Gaussian fame), and he in turn inspired, amongst others, James Clerk Maxwell, Lord Kelvin and Bernhard Riemann, Poincare, Einstein and nowadays John Conway and Ed Witten. So in terms of influence, Listing was hardly a nobody!